В мире информационных технологий конечные поля Галуа GF(2m) имеют огромное практическое значение [1]. В частности, важнейшие алгоритмы обнаружения и исправления искажения информации в системах хранения и сетях передачи данных, использующие коды Рида-Соломона, а также криптографические алгоритмы (например, AES – Advanced Encryption Standard), защищающие информацию от несанкционированного доступа, базируются на арифметике конечных полей Галуа GF(2m).
Однако для эффективной программной и аппаратной реализации алгоритмов, также необходима быстродействующая аппаратная реализация арифметики поля Галуа GF(2m). В частности, для ускорения операций умножения и деления элементов необходимы специальные подходы к разработке быстрой параллельной схемы умножения элементов и нахождения мультипликативной инверсии элемента для операции деления.
В рамках научных исследований в области надежности систем хранения, передачи и обработки данных [3–9], а также методов информационного резервирования [2, 10], автором была исследована эффективная аппаратная схема быстрого умножения, и на базе нее была разработана схема арифметического процессора для поля Галуа GF(2m).
Арифметика поля Галуа GF(2m). Поле Галуа GF(2m), по определению являющееся полем многочленов вида 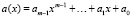 ,
, 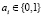 , образуется на базе простого поля Галуа GF(2) и нормированного примитивного неприводимого многочлена m-й степени:
, образуется на базе простого поля Галуа GF(2) и нормированного примитивного неприводимого многочлена m-й степени: 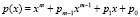 ,
, 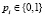 . Особо отметим, что элементы поля можно также рассматривать как m-разрядные двоичные числа
. Особо отметим, что элементы поля можно также рассматривать как m-разрядные двоичные числа 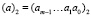 , и более того, для компактной формы представления записывать двоичные эквиваленты элементов поля в десятичной форме (а)10.
, и более того, для компактной формы представления записывать двоичные эквиваленты элементов поля в десятичной форме (а)10.
Например, поле Галуа GF(24) образуется при помощи неприводимого многочлена 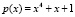 , и его элементы можно рассматривать как многочлены, так и соответствующие двоичные и десятичные эквиваленты:
, и его элементы можно рассматривать как многочлены, так и соответствующие двоичные и десятичные эквиваленты:
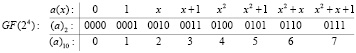
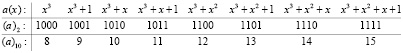
Отметим, что в базовом простом поле GF(2) для элемента 0 обратным элементом по сложению является сам элемент 0, также как и для элемента 1 обратным элементом по сложению является сам элемент 1. Соответственно, как сложение, так и вычитание элементов простого поля GF(2) фактически сводятся к одной и той же операции суммирования по модулю 2, и обозначается символом 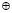 .
.
Тогда, при сложении и вычитании элементов поля GF(2m) мы имеем сложение соответствующих коэффициентов многочленов по модулю 2 (при представлении в виде многочленов) или побитовое сложение по модулю 2 соответствующих разрядов двоичных чисел (при представлении в виде двоичных чисел):
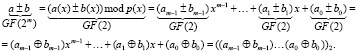 (1)
(1)
Пример. Найдем сумму элементов расширенного поля GF(24), представленных в виде соответствующих чисел «13» и «7» в десятичной системе счисления. Имеем,
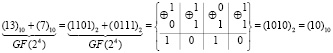 .
.
Быстрое умножение и деление элементов поля GF(2m). Для построения быстрых и компактных умножителей следует использовать классическое определение операции умножения элементов поля Галуа GF(2m), представленных в виде многочленов с коэффициентами из простого поля GF(2):
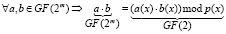 .
.
Рассмотрим умножение элементов на примере поля Галуа GF(24), образованного при помощи примитивного неприводимого многочлена 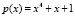 . Имеем следующее:
. Имеем следующее:
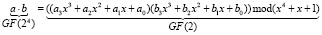 .
.
После перемножения многочленов и вычисления остатка по модулю 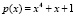 в общем виде получаем:
в общем виде получаем:
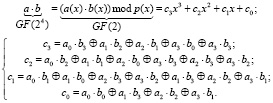
Таким образом, мы имеем m аддитивных функций для вычисления коэффициентов 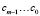 . Функции содержат слагаемые в виде произведений коэффициентов ai∙bj, где
. Функции содержат слагаемые в виде произведений коэффициентов ai∙bj, где 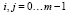 . Поскольку мы имеем дело с полями GF(2m), являющиеся расширением базового простого поля GF(2), то произведение коэффициентов эквивалентно логическому умножению (конъюнкции).
. Поскольку мы имеем дело с полями GF(2m), являющиеся расширением базового простого поля GF(2), то произведение коэффициентов эквивалентно логическому умножению (конъюнкции).
Для аппаратной реализации таких функции удобнее использовать специализированные программируемые логические матрицы (ПЛМ), содержащие в себе логические элементы «И» с двумя входами и многовходовые сумматоры по модулю 2.
Ниже на рис. 1 приведена функциональная схема умножителя элементов поля GF(24), образованного на базе примитивного неприводимого многочлена 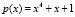 .
.
Входы сумматоров в соответствии с аддитивными функциями подключаются к выходам логических элементов «И», формирующих соответствующие произведения коэффициентов ai∙bj. Незадействованные входы сумматоров подключаются к «земле».
Теперь обобщим вышеприведенный пример для общего случая умножения элементов поля Галуа GF(2m), m ≥ 2, образованного на базе заданного примитивного неприводимого многочлена 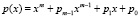 , в виде итерационной процедуры, в которой за m итераций выводятся m формул для расчета всех коэффициентов многочлена-произведения:
, в виде итерационной процедуры, в которой за m итераций выводятся m формул для расчета всех коэффициентов многочлена-произведения:
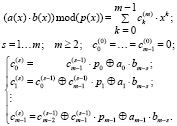 (2)
(2)
Следует особо отметить, что итерационный вывод прямых формул осуществляется лишь один раз на этапе проектирования аппаратной реализации, и далее формулы аппаратно реализуются в коммутационной матрице соединений между выходами m2 двухвходовых элементов «И» и входы m элементов сумматоров по модулю 2.
Что касается операции деления элемента a на ненулевой элемент b поля, то ее можно свести к операции умножения на обратный элемент b–1.
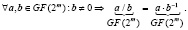 (3)
(3)
Вычисление обратного элемента по умножению для максимального быстродействия, очевидно, лучше всего опять же осуществлять табличным способом, используя ПЗУ емкостью 2mm бит. Что касается формирования самой таблицы обратных элементов на этапе проектирования, то ее можно подготовить заранее, используя расширенный алгоритм Евклида для многочленов, который сводит решение уравнения
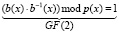 ,
,
где b–1(x) разыскиваемый обратный многочлен по умножению, к нахождению многочленов g(x) и h(x), а также наибольшего общего делителя 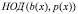 для многочленов b(x) и p(x) таких, что
для многочленов b(x) и p(x) таких, что
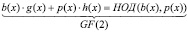 .
.
Поскольку мы имеем дело с полем, то для любого ненулевого многочлена 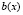 алгоритм в качестве
алгоритм в качестве 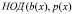 дает скаляр
дает скаляр 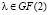 (многочлен нулевой степени), и в нашем «двоичном» случае скаляр будет равен строго λ = 1, так как в базовом простом поле GF(2) существует только один ненулевой элемент – это единица. Соответственно, многочлен g(x), находимый алгоритмом, и является искомым обратным многочленом по умножению, то есть
(многочлен нулевой степени), и в нашем «двоичном» случае скаляр будет равен строго λ = 1, так как в базовом простом поле GF(2) существует только один ненулевой элемент – это единица. Соответственно, многочлен g(x), находимый алгоритмом, и является искомым обратным многочленом по умножению, то есть 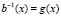 .
.
Приведем для примера таблицу обратных элементов для элементов поля GF(24), представленных для компактности в виде десятичных и двоичных эквивалентов элементов.

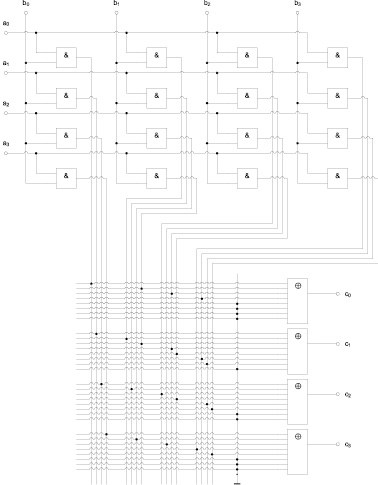
Рис. 1. Функциональная схема умножителя элементов поля Галуа GF(24) на базе специализированной логической матрицы
Ниже на рисунке 2 представлена функциональная схема арифметического процессора для поля Галуа GF(2m), использующего таблицу обратных элементов по умножению, хранящуюся в ПЗУ и умножитель элементов, который, как было рассмотрено выше, реализуется на базе специализированной программируемой логической матрицы.
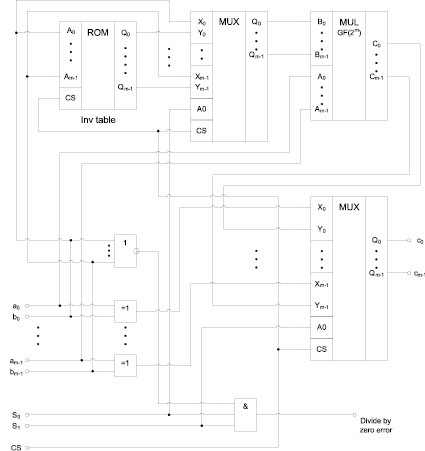
Рис. 2. Функциональная схема арифметического процессора для поля Галуа GF(2m) с использованием умножителя элементов и таблицы обратных элементов по умножению
В схеме процессора используются два m-битных мультиплексора 2 → 1. Нижний мультиплексор коммутирует свои входы с выходами логических элементов XOR при управляющем сигнале S1 = 0 (режим операций сложения / вычитания), и с выходами умножителя при S1 = 1 (режим операций умножения / деления). При S1 = 0, управляющий сигнал S0 не играет никакой роли (сложение и вычитание сводится к одной и той же операции «побитового» XOR). При S1 = 1, сигнал S0 управляет верхним мультиплексором, который при S0 = 0 подключает линии 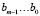 напрямую к умножителю элементов, что соответствует операции умножения на операнд b, а при S0 = 1 подключает выходы ПЗУ, преобразующего операнд b в его обратный элемент по умножению, что соответствует операции деления на операнд b. В схеме процессора также предусмотрена цепь обнаружения нулевого делителя (b = 0) в режиме операции деления (S1 = 1 и S0 = 1).
напрямую к умножителю элементов, что соответствует операции умножения на операнд b, а при S0 = 1 подключает выходы ПЗУ, преобразующего операнд b в его обратный элемент по умножению, что соответствует операции деления на операнд b. В схеме процессора также предусмотрена цепь обнаружения нулевого делителя (b = 0) в режиме операции деления (S1 = 1 и S0 = 1).
Арифметический процессор на базе умножителя и таблицы обратных элементов требует одного ПЗУ емкостью 2mm бит, и умножителя, состоящего из m2 двухвходовых логических элементов «И», m многовходовых сумматоров по модулю 2, и коммутационной матрицы размером 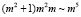 . Если коммутационную матрицу тоже рассматривать как «постоянную память», то, очевидно, что ее размер составляет m5.
. Если коммутационную матрицу тоже рассматривать как «постоянную память», то, очевидно, что ее размер составляет m5.
Заключение
Таким образом, в данной статье рассмотрены поля Галуа GF(2m), их арифметика, операции сложения, а также умножения и деления на базе быстрого умножения и табличного инвертирования элементов. Также рассмотрена схема быстрого умножения, а также предлагаемая автором схема арифметического процессора для поля Галуа.
Полученные результаты были использованы автором для разработки обучающей программы и лабораторных стендов для изучения студентами технических специальностей технологии кодирования информации при применении кодов Рида-Соломона.

