О численном методе, алгоритме и комплексе программ моделирования волн напряжений
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости (рис. 1) имеют вид
, 
,
,
, 
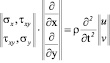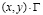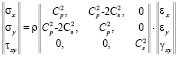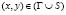, (1)
где σx, σy и τxy – компоненты тензора упругих напряжений; εx, εy и γxy – компоненты тензора упругих деформаций; u и v – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ – плотность материала;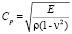 
– скорость продольной упругой волны; 
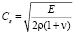– скорость поперечной упругой волны; v – коэффициент Пуассона; Е – модуль упругости; 
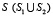– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
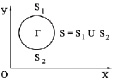
Рис. 1. Некоторое тело Г в прямоугольной декартовой системе координат XOY
Принимая во внимание определение матриц и векторов для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
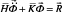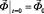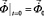, (2)
где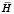 
– матрица инерции; 
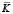– матрица жесткости; 
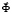– вектор узловых упругих перемещений; 
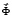– вектор узловых упругих скоростей перемещений; 
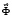– вектор узловых упругих ускорений; 
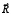– вектор узловых упругих внешних сил.
Соотношение (2) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Для интегрирования уравнения (2) конечноэлементным вариантом метода Галеркина приведем его к следующему виду
, 
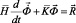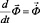. (3)
Интегрируя по временной координате соотношение (3) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
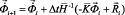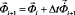. (4)
Шаг по временной переменной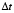 
определяем из следующего соотношения
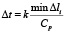
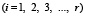, (5)
где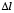 
– длина стороны конечного элемента; r – общее число конечных элементов.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость явной схемы.
Разработанная методика позволяет решать задачи о взаимодействии сложных деформируемых тел с волновыми нагрузками. С помощью полученных разработок можно определять волны напряжений в деформируемых телах. На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных волновых воздействиях. При разработке комплекса программ использовался алгоритмический язык Фортран-90. Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений.
Решение задачи о воздействии плоской продольной упругой волны в виде функции Хевисайда на бесконечную полосу
Некоторая информация о численном моделировании нестационарных волн напряжений в твердых деформируемых областях приведена в следующих работах [1–10].
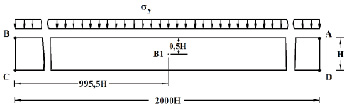
Рис. 2. Постановка задачи о стоячих волнах в бесконечной полос
В работах [1–2, 4–6, 8, 10] приведена некоторая информация о физической достоверности и математической точности моделирования нестационарных волн напряжений в деформируемых телах с помощью рассматриваемого численного метода, алгоритма и комплекса программ.
Рассмотрим задачу о воздействии плоской продольной упругой волны в виде ступенчатого импульса (функция Хевисайда) на бесконечную полосу.
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения было принято следующее допущение: 1 кгс/см2 ≈ 0,1 МПа.
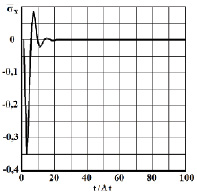
Рис. 3. Нормальное напряжение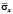 
во времени 0 ≤ n ≤ 100 в точке B1
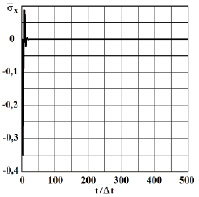
Рис. 4. Нормальное напряжение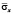 
во времени 0 ≤ n ≤ 500 в точке B1
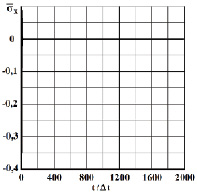
Рис. 5. Нормальное напряжение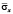 
во времени 0 ≤ n ≤ 1990 в точке B1
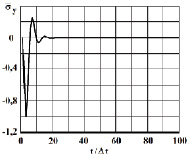
Рис. 6. Нормальное напряжение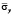 
во времени 0 ≤ n ≤ 100 в точке B1
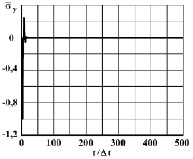
Рис. 7. Нормальное напряжение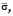 
во времени 0 ≤ n ≤ 500 в точке B1
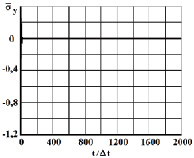
Рис. 8. Нормальное напряжение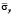 
во времени 0 ≤ n ≤ 1990 в точке B1
На границе пластинки AB (рис. 2) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 3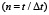 
изменяется линейно от 0 до P, а при n ≥ 3 равно P (P = σ0, σ0 = – 0,1 МПа (– 1 кгс/см2)).
Граничные условия для контуров BC и AD при t > 0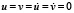 
. Отраженные волны от контуров BC и AD не доходят до исследуемых точек. Контур CD свободен от нагрузок.
Исследуемая расчетная область имеет 4002 узловые точки. Решается система уравнений из 16008 неизвестных.
Для примера на рис. 3–5 представлено изменение нормального напряжения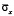 
(
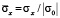) во времени n в точке B1. Для примера на рис. 6–8 представлено изменение нормального напряжения 
(
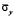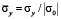) во времени n в точке B1.
Получены нормальные напряжения в характерной области бесконечной полосы. Отраженные растягивающие волны от свободной поверхности бесконечной полосы накладываются на сжимающие волны от импульса. Интерференция прямых и отраженных волн приводит к нулевому напряженному состоянию в бесконечной полосе при воздействии ступенчатой функции.