Высокотемпературные сверхпроводники (ВТСП) демонстрируют аномальное поведение в смешанном состоянии. В частности, это выражается в том, что знак коэффициента Холла в смешанном состоянии может быть противоположен его знаку в нормальном состоянии [1]. Уравнения, полученные в рамках классических моделей Нозьера-Винена (NV) и Бардина-Стефана (BS) (основанных на анализе динамики вихрей Абрикосова) [2], не позволяют описать смену знака коэффициента Холла RH. Для объяснения данного эффекта был предложен целый ряд моделей [3], однако до сих пор как происхождение, так и причины наличия или отсутствия аномалии, связанной со сменой знака RH в конкретном сверхпроводнике, остаются неясными.
В работе Хирша и Марсильо [4] для объяснения смены знака эффекта Холла в смешанном состоянии была предложена двузонная модель, в которой предполагалось наличие электронов и дырок. Данные исследования транспортных свойств, эксперименты по фотоэмиссионной спектроскопии с угловым разрешением (ARPES) [5] и результаты исследования магнитосопротивления в сильных магнитных полях [6] показывают, что свойства нормального состояния электронного ВТСП Nd2-xCexCuO4+δ определяются как электронами, так и дырками.
Для ВТСП также характерно то, что зависимости верхнего критического поля от температуры Hc2(T) существенно отличаются от зависимостей Hc2(T) для обычных низкотемпературных сверхпроводников [7]. В работе [8] показано, что магнитосопротивление в нормальном состоянии пленок Nd1.85Ce0.15CuO4+δ с оптимальным отжигом можно количественно описать в рамках модели с двумя типами носителей, если предположить сосуществование электронно-подобной и дырочно-подобной зон.
2.1 Эффект Холла в смешанном состоянии
В настоящей работе представлены результаты измерений магнитосопротивления и коэффициента Холла в смешанном и нормальном состояниях в недолегированных (х = 0,14), оптимально-легированных (х = 0,15) и перелегированных (x = 0,17 и 0,18) монокристаллических пленках электронно-легированного сверхпроводника Nd2-xCexCuO4+δ с различным содержанием кислорода δ (степенью беспорядка) в магнитных полях до 90 кЭ (H ║ c; J ║ ab) в интервале температур Т = (0,4 – 40) К.
В смешанном (резистивном) состоянии (при Hp< H <Hc2, Hp- поле депиннинга вихревой решетки, Hc2 – верхнее критическое поле), в котором конечное значение сопротивления является следствием движения вихревых нитей под действием силы Лоренца, для электронно-легированного сверхпроводника Nd2-xCexCuO4+δ обнаружена аномальная смена знака эффекта Холла в магнитных полях ниже Hc2: с отрицательного на положительный для х = 0,14, 0,15 (рис. 1) и с положительного на отрицательный для х = 0,17, 0,18 (рис. 2).
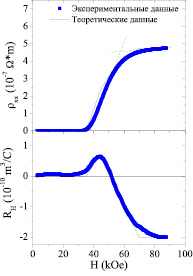
Рис. 1. Экспериментальные и теоретические зависимости ρ(H) и RH(H) при T = 4,2 К для образца Nd2-xCexCuO4+δ с x = 0,15 и оптимальным отжигом
В рамках схемы, основанной на классической модели Друде для нормального состояния и полуфеноменологической модели Бардина-Стефена для смешанного состояния сверхпроводника, модифицированных с учетом сосуществования электронов и дырок, оказалось возможным количественно описать всю совокупность наблюдаемых магнитополевых зависимостей продольной и холловской компонент сопротивления в системе Nd2-xCexCuO4+δ (для x = 0,14÷0,18 и различных значений δ). По аналогии с работой [4] мы предполагаем, что два типа носителей имеют существенно различные сверхпроводящие щели и, как следствие, существенно различные значения виртуального верхнего критического поля. Подробный вывод уравнений для расчета приведен в работе [9].
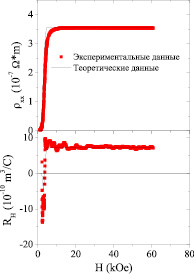
Рис. 2. Экспериментальные и теоретические зависимости ρ(H) и RH (H) при температуре 4,2 К для образца Nd2-xCexCuO4+δ с x = 0,18 и оптимальным отжигом
Результаты анализа зависимостей коэффициента Холла RH(H) и удельного сопротивления от магнитного поля ρ(H) при T = 4,2 К для образцов Nd2-xCexCuO4+δ в рамках данной модели приведены на рис. 1 для x = 0,15 и рис. 2 для x = 0,18. Найденные при расчете значения подгоночных параметров для двух типов носителей (концентраций электронов (n) и дырок (p) при соотношении подвижностей μn /μp ≈ 1) представлены в таблице.
Величины подгоночных параметров для двух типов носителей
|
x |
n, см-3 |
p, см-3 |
|
0,14 |
2,3·1020 |
4,9·1019 |
|
0,15 |
4,3·1021 |
5,4·1021 |
|
0,18 |
3,5·1020 |
2,8·1021 |
Из таблицы видно, что для недолегированного образца (x = 0,14) рассчитанные концентрации электронов и дырок находятся в соотношении p<<n; для образца с оптимальным легированием (x = 0,15) p≃n; для перелегированного образца (x = 0,18) p>>n, что соответствует результатам, полученным из данных ARPES [5] и из частот осцилляций Шубникова-де-Гааза [6] для различных образцов Nd2-xCexCuO4+δ.
2.2 Температурные зависимости верхнего критического поля
В данной работе представлены также результаты измерений резистивным методом (из измерений электросопротивления в магнитном поле) верхнего критического поля (Hс2) в зависимости от температуры (Т) в монокристаллических пленках Nd2-xCexCuO4+δ /SrTiO3 с х = 0,14 и 0,15 при различной степени беспорядка (δ) в магнитных полях до 90 кЭ в интервале температур T = (0,4 – 40) К в ЦКП «Испытательный центр нанотехнологий и перспективных материалов» ИФМ УрО РАН.
Обнаружено, что в оптимально легированных пленках Nd2-xCexCuO4+δ с х = 0,15 и различной степенью беспорядка (δ) наблюдается два вида зависимостей Hc2(T):
1. Аномальные зависимости с положительной кривизной Нс2(Т) в оптимально и не оптимально отожженных пленках и
2. БКШ-зависимости в пленке без отжига (рис. 3).
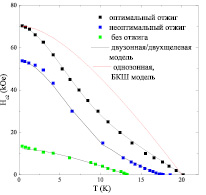
Рис. 3. Экспериментальные и теоретические зависимости верхнего критического поля от температуры для образцов Nd2-xCexCuO4+δ с x = 0,15 и разным отжигом
Температурные зависимости верхнего критического поля для пленок недолегированного Nd2-xCexCuO4+δ с х = 0,14 (в непосредственной близости от антиферромагнитной фазы) имеют аномальную положительную кривизну для всех режимов отжига (рис. 4).
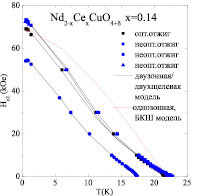
Рис. 4. Экспериментальные и теоретические зависимости верхнего критического поля от температуры для образцов Nd2-xCexCuO4+δ с x = 0,14 и разным отжигом
На рис. 3 и 4 представлены также теоретические зависимости Hc2(T) для образцов Nd2-xCexCuO4+δ с x = 0,15 и с x = 0,14. Для сравнения показано, что кривая, полученная в рамках стандартной однозонной модели Бардина–Купера–Шриффера (БКШ) для обычных сверхпроводников, не описывает экспериментальные зависимости.
Расчеты показали, что все наблюдаемые зависимости Hc2(T) можно непротиворечивым образом объяснить на основе двузонной/двухщелевой модели сверхпроводника в грязном пределе (модель Гуревича [10]), варьируя соотношение коэффициентов диффузии двух типов носителей (электронов и дырок). При этом, в соответствии с анализом работы [10], установлено, что температура сверхпроводящего перехода всегда определяется электронами, в то время как значение верхнего критического поля при низких температурах, Hc2 (T → 0), может определяться как электронами, так и дырками в зависимости от соотношения их коэффициентов диффузии в данном образце.
Выводы
Таким образом, проведенный анализ влияния легирования (и степени нестехиометрического беспорядка) на изменение магнитополевой зависимости тензора электросопротивления в рамках модели проводимости Друде для нормального состояния и полуфеноменологической модели BS для смешанного состояния показал, что в процессах переноса заряда в номинально электронно-легированном сверхпроводнике Nd2-xCexCuO4+δ участвуют два типа носителей заряда с противоположным знаком – электроны и дырки.
Показано, что экспериментально наблюдаемое изменение кривизны Hc2(T) можно объяснить на основе модели двузонного/двухщелевого сверхпроводника в грязном пределе для различного соотношения коэффициентов диффузии электронов и дырок, что также свидетельствует о существовании как электронного, так и дырочного вкладов в явления переноса номинально электронно-легированного сверхпроводника Nd2-xCexCuO4+δ.
Работа выполнена в рамках государственного задания по теме «Электрон» № 01201463326 при частичной финансовой поддержке программы фундаментальных исследований УрО РАН (грант № 15-8-2-6) и РФФИ (грант № 15-02-02270).

