Наибольший интерес представляет метод моделирования волатильности, отнесенный в построенной классификации к эконометрическим моделям. К появлению в начале 80-х годов класса моделей авторегрессионной условной гетероскедастичности (autoregressive conditionally heteroskedastic – ARCH) привело изучение закономерностей изменений волатильности. Суть модели состоит в следующем. Предположим, имеется регрессия временного ряда yt на другие временные ряды (все ряды предполагаются стационарными):
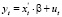. (1)
Из эмпирических наблюдений за поведением достаточно большого количества временных рядов, носивших, в основном, финансовый характер, было замечено, что наблюдения с большими и малыми отклонениями от средних имеют тенденцию к образованию кластеров, то есть периоды «спокойного» и «возмущенного» состояний рынка чередуются. Так как показатели инвестиционных процессов относятся к финансовым, и имеют возможность расчета доходности, то такие модели представляются применимыми.
В работе (Engle, 1982) был предложен следующий способ моделирования этого явления. Пусть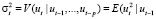 
,…, ut-p) – условная дисперсия ошибок ut (как обычно, E(ut|ut-1,…, ut-p) = 0). Эффект «кластеризации» возмущений можно объяснить следующей моделью зависимости условной дисперсии ошибок ut от предыстории:
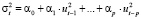. (2)
Процесс (1) и (2) называется авторегресионной условно гетероскедастичной моделью порядка p, ARCH(p).
Простейшая модель такого рода, ARCH(1), имеет следующий вид:
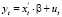
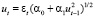
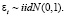(3)
В этой модели условная дисперсия ошибок зависит от времени: V(ut|ut–1) =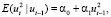 
в то время как безусловная дисперсия ошибок не зависит от времени: V(ut) = V(ut–1) = α0/(1–α1). Таким образом, модель ARCH(1) удовлетворяет всем условиям классической линейной регрессионной модели и МНК-оценки являются наиболее эффективными линейными оценками.
Идея, лежащая в основе ARCH-модели, заключается в различии между условными и безусловными моментами второго порядка, тогда как безусловные вариации и ковариации постоянны, условные моменты нелинейно зависят от прошлых состояний и развиваются во времени. За последние двадцать лет были разработаны многочисленные модификации базовой модели Энгла, в частности M-ARCH, F-ARCH, T-ARCH, и примеры применения ее к финансовым и макроэкономическим временным рядам. В результате выделился целый набор более совершенных моделей, позволяющих отказаться от предположений о независимости волатильности от своих предыдущих значений и учесть автокорреляцию в них. В частности, появились так называемые GARCH-модели (general autoregressive conditional heteroskedastic – GARCH). Как видно из названия, они учитывают корреляционную зависимость с помощью авторегрессии значений волатильности при условии ее гетероскедастичности [2].
Данная модель подразумевает существенную зависимость волатильности от другой случайной величины с учетом времени. GARCH-модель является более сложной, по сравнению с такими моделями волатильности, как равновзвешенное и экспоненциально взвешенное скользящее среднеквадратическое отклонение, о чем свидетельствуют сложный подход к характеристике волатильности. GARCH-модель была предложена в 1986 году Боллерслевом, согласно предположениям которого дисперсия на момент времени t зависит не только от финансовых результатов, но и от условной дисперсии ошибок за предыдущий момент времени:
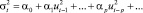
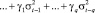. (4)
Такая модель называется обобщенной авторегрессионной условно гетероскедастичной порядка p, q, GARCH(p,q). Существенным преимуществом GARCH-модели признается ее свойство быстрого реагирования на любые наблюдаемые изменения в параметрах инвестиционного процесса и быстрого восстановления после сильных его колебаний.
Значение коэффициентов q и p зависит от параметров, рассматриваемых временных серий и производительности модели при данных коэффициентах. В большом количестве финансовых моделей эти коэффициенты принимаются за единицу, что позволяет оценить около 95 % волатильности доходности, показывая лучшие результаты, чем различные взвешенные модели [1]. Данная модель имеет ряд модификаций, связанных с настройкой модели под определенные требования, таких как A-GARCH модель (ассиметричная GARCH-модель), или более сложная E-GARCH (экспоненциальная GARCH-модель), разработанная Д. Нельсоном в 1991 году.
Меры чувствительности, в отличие от индикаторов и моделей волатильности, информируют о влиянии на доходность различных переменных (факторов). В итоге количество применяемых мер чувствительности зависит от количества анализируемых факторов риска, что создает основу для расчета критических значений и определения границ областей безрискового инвестирования.
Параметры чувствительности можно представить графически с помощью профиля риска, в связи с чем анализ рисков называют также профилированием риска. Профиль риска (risk profile) – это график зависимости изменения экономического показателя (V), например стоимости данного финансового инструмента, от изменения влияющего фактора (p) (курса, процентной ставки, цены базового актива, стоимостей иных товаров или ценных бумаг, объемов торгов и так далее) [1].
Помимо этого, необходимо подчеркнуть фундаментальные отличия концепций мер изменчивости и чувствительности. Меры изменчивости направлены только на измерение последствий риска, проявляющегося в дисперсии доходности, а меры чувствительности позволяют оценить влияние факторов риска [3].
Существенной и широко известной мерой чувствительности доходности инвестиций считается показатель систематического рыночного риска – бета-коэффициент (β), использующийся в качестве одной из мер рыночного риска:
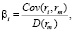(5)
где βi – бета-коэффициент i-го актива;
Cov(ri,rm) – ковариация случайных величин доходности i-го актива и рынка (индекса);
D(rm) – дисперсия доходности рынка.
Этот коэффициент отражает степень влияния рынка на доходность инвестиций и применим только для оценки риска инвестиций, имеющих симметричную кривую доходности.
Чувствительность инвестиционного процесса к изменению значений некоторого базового показателя измеряется коэффициентом дельта. Дельта измеряет величину изменения параметра данного инвестиционного процесса при малом изменении базового ценового фактора (например, ставки процента):
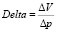, (6)
где V – значение стоимостного параметра данного инвестиционного проекта, либо суммарных инвестиций региона;
p – базовый фактор.
Если изобразить данную зависимость некоторой линией, то дельта характеризует угол наклона, при этом ее величина равна тангенсу этого угла.
В случае наличия фиксированного инвестиционного дохода чувствительность к движению процентных ставок измеряется дюрацией:
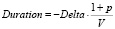, (7)
где обозначения, как в (6).
Показатели риска, представляющие собой производные второго порядка, называются выпуклостью в случае наличия фиксированного инвестиционного дохода, и коэффициентом гамма при нелинейной форме дохода от инвестиционной деятельности. Выпуклость измеряет изменчивость дюрации по мере изменения процентной ставки. Показатель гамма (Γ, gamma) измеряет изменение дельты при изменении базового ценового фактора:
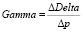. (8)
Гамма измеряет тот же риск, что и выпуклость. Если график зависимости стоимости инвестированных активов от базового ценового фактора выпуклый, то гамма положительна, при вогнутом графике гамма отрицательна, а если профиль риска – прямая линия, то гамма равна нулю. Оба показателя измеряют чувствительность второго порядка (или квадратичную чувствительность) к изменениям финансовых переменных [1].
Одним из косвенных показателей инвестиционного риска служит величина премии за риск – разность доходности данного типа инвестиций ri, которому присущ риск, и доходности безрисковых (условно безрисковых) вложений rf.
В реальности премии за риск инвестиций в конкретные активы могут отклоняться от расчетных премий за систематический риск этих активов, и величина этих отклонений может быть охарактеризована как несистематический (специфический) риск инвестиций в активы, который описывается альфа-коэффициентом (α), показывающим переоценку или недооценку рынком систематического риска для данного актива:
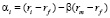, (9)
где ri – доходность i-ого актива;
rf – безрисковая доходность;
rm – ожидаемая рыночная доходность;
βi – бета-коэффициент, определяется также как в (5).
Существует множество иных показателей риска, традиционно применяемых по отношению к производным инструментам на финансовых рынках, которые могут, однако, использоваться при оценке инвестиционного риска на региональном уровне, обозначаемых в основном греческими буквами, поэтому в целом они иногда называются «греческими» (the «Greeks»).
Вега (vega) – показатель риска измеряющий изменение стоимости инвестированного актива при изменении волатильности базового ценового фактора:
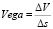. (10)
Показатель изменения гаммы при изменении базового ценового фактора носит название «скорость» (speed):
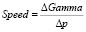. (11)
Если дельта – это первая производная функции стоимости инструмента по базовому ценовому фактору, то гамма – вторая производная, а скорость – производная третьего порядка. Скорость позволяет следить за ростом гаммы и дельты.
Показатель, измеряющий изменение дельты по мере изменения времени до исполнения контракта, называется «очарование» (charm):
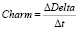. (12)
Разрыв (gap) срочности определяется как разность суммы процентных активов данной срочности и процентных пассивов данной срочности. Для каждого диапазона можно вычислить величину такого разрыва:
Gapt = At – Lt, (13)
где t – разрыв срочности;
At – сумма процентных активов данной срочности;
Lt – сумма процентных пассивов данной срочности.
Можно рассчитать кумулятивный разрыв (cumulative gap) накопленным итогом разрывов для каждой срочности. Кумулятивный разрыв представляет собой разрыв для диапазона, включающего в себя все предыдущие диапазоны, начиная с первого, со срочностью t0:
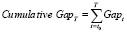, (14)
где t0 – первый диапазон срочности;
T – время.
Коэффициент отношения разрыва к общей величине активов (gap ratio) для разрывов и кумулятивных разрывов рассчитывается соответственно:
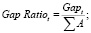(15)
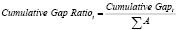. (16)
С помощью анализа разрывов срочной структуры активов и пассивов можно также исследовать риск недостаточной балансовой ликвидности, то есть недостаточности денежных и других быстро оборачиваемых активов для покрытия потребностей в оборотных средствах и обеспечения платежеспособности фирмы [1].
К другим статистическим мерам уровня инвестиционного риска можно отнести: полувариацию, стандартное полуотклонение, учитывающие только отрицательные отклонения доходности от ожидаемого значения, а также вероятность убытков (недостижения требуемого уровня), то есть получения отрицательной или нулевой доходности.
Среди моделей и методов оценки уровня инвестиционного риска, в частности для оценки величины совокупных убытков, также применяется теория игр (в условиях неопределенности с ориентацией на наихудший вариант), метод статистического моделирования Монте-Карло, методы теории массового обслуживания и линейного программирования.
Для всесторонней количественной и качественной оценки инвестиционного риска в настоящее время в мире все активнее используется методология Value-at-Risk (VaR). Концепция рисковой стоимости VaR прочно завоевала позиции в финансовом мире как распространенный методологический стандарт для оценки рыночных рисков. Метод расчета величины VaR представляет собой вероятностно-статистический подход для определения соотношения ценовых показателей и риска, основным понятием в нем является распределение вероятностей, где все возможные величины изменений рыночных факторов связаны с их вероятностями. Ключевыми параметрами VaR являются период времени, на который рассчитывается риск, и заданная вероятность того, что потери не превысят определенной величины. Методология VaR обладает рядом других несомненных преимуществ, так как позволяет:
– оценить риск в терминах возможных потерь, соотнесенных с вероятностями их возникновения;
– измерить различные по генезису инвестиционные риски универсальным образом;
– агрегировать отдельные риски в единую величину, учитывая при этом информацию о количестве инвестиционных проектов, волатильности и периоде проекта [4]. К другим важным достоинствам VaR относятся: простота и наглядность расчётов, консолидация информации, возможность сравнительного анализа потерь и соответствующих им рисков.
VaR – статистическая оценка максимально возможных потерь данного портфеля финансовых инструментов при заданном распределении за определенный период времени во всех случаях, за исключением заранее заданного малого процента ситуаций.
Рассмотренные методы и модели дают возможность с той или иной точностью оценить инвестиционный риск либо в полной мере, либо с учетом какого-то его аспекта. Однако все они используются для оценки рисков либо практически любой природы, либо генетически восходят к оценке инвестиционных портфельных рисков, поэтому, базируясь на статистике, в частности, на данных временных рядов, более применимы для динамической оценки риска, то есть для анализа инвестиционных данных региона в целом. Что же касается агрегированных оценок инвестиционных рисков проектов, локализованных в регионе, то их рекомендуется измерять с помощью традиционных для этого методов.