Принято считать [3], что коэффициент теплопроводности металлов складывается из двух составляющих
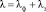 , (1)
, (1)
где λф, λэ – коэффициенты теплопроводности фононов и электронного газа соответственно.
Под фононами понимают минимальную порцию энергии, которую может поглотить или испустить кристаллическая решётка при тепловых колебаниях в случае перехода с одного энергетического уровня на другой. Тогда поле упругих волн, заполняющих кристалл, можно трактовать как газ, образованный квантами нормальных колебаний решётки, т.е. фононами [1].
Вычисление фононовой или решёточной теплопроводности металлов и сплавов как части их общей теплопроводности, определение её доли при различных состояниях металлов и сплавов (монокристаллическое, поликристаллическое, мелкозернистое, крупнозернистое и т.п.) является актуальной практической задачей определения оного из важнейших теплофизических свойств конструкционных и инструментальных материалов.
Для решения этой задачи выбран методологически принципиально новый термодинамический метод – нелокальная версия термодинамики. Предложенная Майковым В.П. нелокальная версия термодинамики [4] позволяет обобщить классическую равновесную и линейную неравновесную термодинамику на новой методологической основе. Основной (и единственной) исходной предпосылкой данного подхода является следующее положение. В качестве макроскопического определения энтропии используем то, которое дает второй закон термодинамики
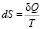 . (2)
. (2)
В силу квантовой природы энергии значение δQ не может быть сколь угодно малым. По смыслу этой величины оно должно быть минимальным макроскопическим значением, которое еще может быть измерено на макроуровне. В качестве ∆Q = δQ примем естественную границу точности измерения количества теплоты – среднее значение теплового шума – kТ, где k – постоянная Больцмана, k = 1,381∙10+ Дж/К.
Если принять значение kТ за минимальное приращение (интервал квантования) количества теплоты
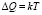 ,
,
то из определения энтропии (2) получим минимальное приращение энтропии
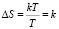 ,
,
то есть константа Больцмана является квантом энтропии.
Используя величину DQ как минимальную энергию в соотношении неопределенностей энергия-время квантовой физики, получим характерный масштаб времени
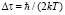 , (3)
, (3)
где 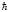 – постоянная Планка,
– постоянная Планка, 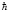 = 1,05∙10–34 Дж∙с.
= 1,05∙10–34 Дж∙с.
Величина Dt (она имеет порядок 10-13∙10-14 с) характеризует минимальный интервал времени, для которого макроскопическое понятие температуры еще сохраняет физический смысл, т.е. этот интервал времени фактически определяет границу между микро и макромиром. Используя уравнение (3) можно сформировать первую неньютоновскую метрику макромира – минимальный линейный размер r и минимальный объём VM распространения электромагнитных волн
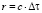 , (4)
, (4)
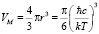 , (5)
, (5)
где с – скорость распространения света в данной среде, м/с.
Данный объём задаёт в пространстве размеры, в пределах которых устанавливается термодинамическое равновесие и для данного объёма справедливы соотношения равновесной термодинамики. Такой объём в нелокальной версии термодинамики принято называть макроячейкой. Состояние макроячейки может быть охарактеризовано с помощью макроскопических термодинамических параметров, таких как температура, давление, энтропия, масса, количество частиц и других. Уже на макроскопическом уровне эти параметры можно рассчитать с конечной долей определенности. Возникающая неопределённость носит объективный характер и связана с тем, что макроячейки постоянно обмениваются между собой элементарными порциями количества теплоты DQ = kT.
Если макроячейка получает элементарную порцию количества теплоты DQ при P = const, то объем, температура и масса макроячейки изменяются на величину
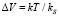 , (6)
, (6)
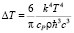 , (7)
, (7)
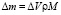 , (8)
, (8)
где kS – адиабатический модуль сжатия, н/м2;
сР – мольная изобарная теплоемкость, Дж/(кмоль К);
ρ – молярная плотность, кмоль/м3;
М – молярная масса, кг/кмоль.
Выбор условия P = const вызван тем, что в состоянии динамического (флуктуационного) равновесия каждая отдельная макроячейка выступает лишь как область пространства, охваченная электромагнитным взаимодействием за время Dt, т.е. макроячейка не является объемом, который был бы физически фиксирован в определенных границах.
Изменение массы макроячейки – элементарная масса Dm содержит меньше одной частицы. Это значит, что элементарную массу можно рассматривать только как квазичастицу, которая в данном случае является акустическим фононом. Этот акустический фонон и отвечает за перенос массы, тепла и импульса в данной среде.
Так как минимальная скорость распространения акустического фонона (квазичастицы) равна скорости распространения звука в данной среде (это можно доказать), то можно ввести вторую неньютоновскую метрику макромира – это радиус упругих взаимодействий между макроячейками
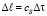 , (9)
, (9)
где cS – скорость звука в данной среде, м/с.
Акустические фононы уже в равновесных условиях участвуют в переносе субстанции (массы, тепла, импульса) между макроячейками. Для получения равновесного потока субстанции можно использовать уравнение Умова-Пойнтинга для случая упругих взаимодействий [2], записанное в интегральной форме
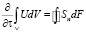 ,
,
где U – плотность субстанции,
Sn – плотность потока субстанции по нормали к поверхности n.
Поскольку параметры в рассматриваемом подходе носят элементарный макроскопический характер, то интегралы можно заменить средними величинами и получить для теплового потока
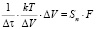 .
.
Откуда находим равновесную плотность потока тепла как плотность потока субстанции
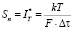 .
.
Поверхность F можно определить, как отношение характерного для упругих взаимодействий объема DV к характерному линейному размеру Dl
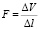 .
.
Тогда выражение равновесного потока тепла окончательно запишется
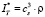 . (10)
. (10)
Чтобы получить неравновесный тепловой поток, воспользуемся линейным приближением и запишем для неравновесного теплового потока в металлическом стержне
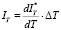 .
.
Здесь величина DТ определяется выражением
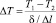 ,
,
где Т1 – температура на одном конце стержня, К;
Т2 – температура на другом конце стержня, К;
δ – длина стержня, м.
Окончательно выражение неравновесного теплового потока в стержне конечной длины получим в виде:
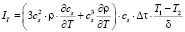 .
.
Полученное выражение для IТ имеет размерность Вт/м2, т.е. размерность плотности теплового потока.
Проводя аналогию с законом теплопроводности (законом Фурье)
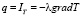 ,
,
можно положить, что
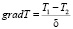 ,
,
тогда
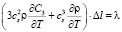 . (11)
. (11)
По идеологии вывода уравнения (11) можно предположить, что полученное с его помощью значение коэффициента теплопроводности даст нам решёточную (фононовую) теплопроводность металлической кристаллической решётки. С целью проверки достоверности полученного выражения проведены расчеты для низкоуглеродистой стали со следующими исходными параметрами.
Плотность вещества с учетом среднего температурного коэффициента объемного расширения b определялась по соотношению
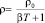 ,
,
где ρ0 = 7800 кг/м3 (сталь 40[5]); β = 4∙10-6 К-1.
Скорость звука представлена в следующем виде:
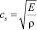 ,
,
где Е – модуль упругости, Па;
r – плотность материала стержня, кг/м3.
Зависимость модуля упругости низкоуглеродистой стали от температуры удалось описать квадратичной зависимостью в виде
Е = – 183441,55 Т2 + 1,238007× ×108 Т + 1,816827×1011 (Па)
Получены следующие значения коэффициента теплопроводности низкоуглеродистой стали при соответствующих температурах в диапазоне от 300 °К до 1073 °К.
Коэффициенты решёточной теплопроводности низкоуглеродистой стали
|
Т, °К |
300 |
373 |
473 |
573 |
673 |
773 |
873 |
973 |
1073 |
|
λ, Вт/(м×К) |
6,78 |
5,25 |
15,35 |
21,64 |
25,27 |
26,69 |
26,29 |
24,23 |
20,65 |
Обсуждение результатов.
Полученные значения меньше, чем приведенные в справочной литературе (так для стали 45 в диапазоне температур Т = 300…600…800 К, l = 79…43…30 Вт/(м×К) [5, с. 343]. Но эти значения в контексте изложенного подхода соответствуют коэффициенту решёточной теплопроводности λреш = λф, и составляют только часть теплопроводности металлического кристалла. Изложенная в литературе качественная тенденция [3], которая говорит о том, что с повышением температуры lреш играет все более существенную роль, подтверждена результатами расчётов. Кроме того, в источнике [1] утверждается, что теплопроводность кристаллической решётки обусловлена ангармоническим характером колебаний атомов, что фактически означает взаимодействие между фононами. Очевидно, что с повышением температуры взаимодействие между фононами возрастает, поэтому зависимость коэффициента теплопроводности от температуры имеет явно выраженный экстремальный характер.
Таким образом, с помощью аналитического вывода выражения для коэффициента теплопроводности и проведенных расчётов подтверждена возможность использования нелокальной версии термодинамики для теоретического определения такого важного термодинамического параметра веществ, как коэффициент решёточной теплопроводности.

