Природа и температурная зависимость поверхностного натяжения жидкостей в течении более чем ста лет исследовались многими авторами [2; 5; 6; 7]. Однако, на сегодняшней день не существуют подходов, или теории поверхностного натяжения жидкостей хотя бы качественно носящих универсальный характер.
В настоящей работе предлагается некий полуфеноменологический подход, позволяющий вычислить температурную зависимость коэффициента поверхностного натяжения жидкостей во всей области температур существования жидкости.
Методами термодинамических циклов [9], а также потенциалов [3] можно показать, что термический коэффициент поверхностного натяжения жидкости, в общем случае, определяется как
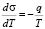, (1)
где q – количество тепла, поглощающееся при обратимом изотермическом изменении единичной площади поверхности, равно разности удельной поверхности энергии и работы при изотермическом расширении поверхности раздела на единицу. Эту величину в дальнейшем будем называть удельной теплотой поверхностообразования (УТП). Очевидно, что УТП является функцией от температуры, т.е. q = q(Т). Если пренебречь этой зависимостью и учесть, что в критической точке (Т = ТК) поверхностного натяжение жидкости равно нулю (σ = σк = 0), то из (1) имеем
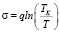. (2)
Выражению (2) можно придать более удобный для практических целей вид. Для этого будем исходит из того, что при х > 0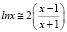 
. Тогда (2) примет следующий вид
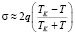. (3)
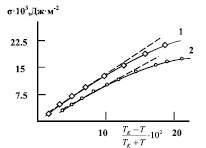
Рис. 1. Зависимость коэффициента поверхностного натяжения от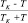 
: 1 – этиловый спирт, 2 – ацетон
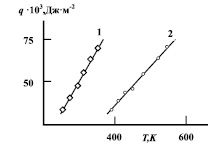
Рис. 2. Температурная зависимость удельной теплоты поверхностообразования (точки-формула (3), сплошные линии – формула (6), 1 – вода, 2 – ацетон)
Поскольку к настоящему времени критические температуры практически всех жидкостей известны, то, в принципе, по значению коэффициента поверхностного натяжения при одной температуре посредством (3) можно вычислить УТП (q), и, тем самым, определить температурную зависимость поверхностного натяжения во всей области существования жидкости. Однако, анализ, проведенный для ряда жидкостей, показал, что вычисленные вышеописанным способом значения поверхностного натяжения значительно (~ 20 %) отличаются от соответствующих экспериментальных значений. Естественно полагать, что это расхождение, в первую очередь, связанно с допущением, сделанным нами при выводе (3), о температурной независимости УТП. При правомерности сделанного предположения, как это следует из (3), в координатах σ = F(TK – T)/(TK + T) должна наблюдаться нелинейная зависимость. В качестве примера (рис. 1) приведены результаты таких сопоставлений для этилового спирта и ацетона. (Экспериментальные значения σ и ТК были заимствованы из [4]). Как видно, в обоих случаях имеет место вышеупомянутая нелинейность. Следовательно, при вычислении σ = σ(Т) по (3) необходимо учесть температурную зависимость УТП q = q(Т).
Температурная зависимость удельной теплоты поверхностообразования, вычисленная посредством (3) по экспериментальным значениям σ и ТК для некоторых жидкостей приведена на рис. 2. Как видно, во всех случаях зависимость q = q(Т) вплоть до критической температуры является линейной, т.е. термический угловой коэффициент УТП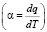 
для каждой жидкости есть постоянная величина и не зависит от температуры. Тогда очевидно, что
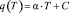. (4)
При температуре плавления твердой фазы выбранной жидкости (Т = Тпл) q обозначим через q0. Тогда из (4) следует, что постоянная интегрирования
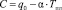. (5)
Из (4) и (5) находим, что
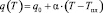. (6)
Подставляя (6) и (1), после интегрирования, получим
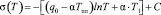. (7)
Поскольку при Т = ТК σ ≡ и
,
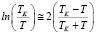то после простых преобразований из (7) имеем:
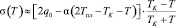. (8)
(8) позволяет при известных q0 и α вычислить температурную зависимость коэффициента поверхностного натяжения во всей области существования жидкости вплоть до критической температуры. Оно является универсальным выражением, т.к. при его выводе не было сделано каких-либо предположений о природе жидкости.
Таблица 1
Значения ТК, Тпл, q0 и α для жидкостей
|
Вещества Параметры |
Этиловый спирт |
Метиловый спирт |
Ацетон |
Вода |
Na |
K |
Rb |
Cs |
Hg |
|
ТК, К |
516 |
513 |
508,8 |
647,3 |
2500 |
2250 |
2100 |
2050 |
1460 |
|
Тпл, К |
158,3 |
175 |
176,5 |
273 |
371 |
337 |
313 |
302 |
234 |
|
q0∙103, Дж/м2 |
– 24,11 |
– 25,61 |
– 15,1 |
32,15 |
59,56 |
20,70 |
26,43 |
28,10 |
-107,45 |
|
α∙105, Дж/К∙м2 |
26,84 |
29,75 |
22,84 |
32,89 |
6,77 |
5,90 |
4,04 |
2,35 |
0,72 |
Таблица 2
Табличные (σТ) и вычисленные (σв) по (8) значения поверхностного натяжения жидких металлов Na и Cs
|
Т, К |
σТ, эрг/см2 |
σв, эрг/см2 |
σв/σТ |
|||
|
Na |
Cs |
Na |
Cs |
Na |
Cs |
|
|
400 |
192,1 |
66,7 |
192,09 |
67,07 |
0,999 |
1,005 |
|
450 |
187,1 |
64,3 |
186,71 |
64,48 |
0,998 |
1,003 |
|
500 |
182,1 |
61,9 |
181,39 |
61,95 |
0,996 |
1,000 |
|
550 |
177,1 |
59,5 |
176,1 |
59,48 |
0,994 |
0,999 |
|
600 |
172,1 |
57,1 |
170,9 |
57,06 |
0,993 |
0,999 |
|
650 |
167,1 |
54,7 |
165,75 |
54,68 |
0,992 |
0,999 |
|
700 |
162,1 |
52,3 |
160,66 |
52,34 |
0,991 |
1,000 |
|
750 |
157,1 |
49,9 |
155,6 |
50,05 |
0,990 |
1,003 |
|
800 |
152,1 |
47,5 |
150,6 |
47,80 |
0,990 |
1,006 |
|
900 |
142,1 |
– |
140,8 |
– |
0,991 |
– |
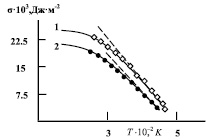
Рис. 3. Температурная зависимость коэффициента поверхностного натяжения: 1 – этиловый спирт, 2 – ацетон; точки-эксперимент, сплошные линии-вычислены по формуле (8)
Как это вытекает из (6), величины q0 и α является для выбранной жидкости постоянными величинами. Поэтому по значениям σ при произвольных двух температурах (полагается, что Тпл и ТК известны) посредством (8) можно вычислить q0 и α, и тем самым, установить явный вид температурной зависимости коэффициента поверхностного натяжения для данной жидкости. Результаты соответствующих вычислений для девяти разных жидкостей приведены в табл. 1–2 и рис. 3.
Как следует из табл. 2 и рис. 3, во всей температурной области существования жидкой фазы табличные и вычисленные по формуле (8) значения поверхностного натяжения достаточно хорошо согласуются между собой. Это, в частности, свидетельствует о приемлемости предложенного нами полуфеноменологического подхода.
Таким образом, в настоящей работе предложен и проанализирован эффективный полуфеноменологический метод, позволяющей по экспериментальным значениям коэффициента поверхностного натяжения жидкости при двух произвольных температурах вычислить температурную зависимость σ = σ(Т) и q = q(Т) вплоть до критической температуры. На примере девяти разных жидкостей установлена универсальность и приемлемость предложенного метода.