В рамках реформы железнодорожного транспорта, утвержденной [1] постановлением Правительства Российской Федерации от 18.05.2001 г. № 384, отдельные направления деятельности ОАО «Российские железные дороги» передаются специально создаваемым для этого дочерним компаниям. Целью реформы является повышение эффективности деятельности ОАО «РЖД», оптимизация расходов и, как следствие, увеличение прибыли от той или иной деятельности. Организация перевозочного процесса базируется на планировании движения поездов на перегонах и размещении, прибывающих поездов на станциях.
Целью данной работы является разработка модели процесса перевозок пригородным железнодорожным транспортом, позволяющей определить узловые станции, рассчитать требуемое количество вагонов поезда, следующего между соответствующими узловыми станциями для снижения технических, материальных и трудовых издержек.
Постановка задачи
Процесс формирования пассажиропотока зависит от многих факторов случайной природы. Если рассматривать процесс формирования пассажиропотока как поток случайных событий, т.е. как простейший поток, то математическое описание данного потока можно получить в виде функции распределения случайных величин. Следовательно, основным методом решения рассматриваемой задачи является теория систем массового обслуживания (СМО) [2]. Теоретическим законом, характеризующим рассматриваемый поток, является распределение Пуассона:
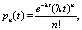
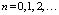 (1)
(1)
где n – число состояний системы, λ – интенсивность потока.
В случае, когда система имеет конечное число состояний [3, 4], вероятности состояний p1(t), р2(t), …рn(t) в момент времени t определяются из системы дифференциальных уравнений, имеющих вид
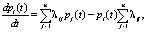
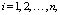 (2)
(2)
где λij pj(t) – поток вероятности перехода из состояния Si в состояние Sj. Указанные уравнения составляются, пользуясь размеченным графом состояний системы и следуя следующему правилу – производная вероятности каждого состояния равна сумме всех потоков вероятности, переходящих из других состояний в текущее, минус сумма всех потоков вероятности, переходящих из текущего состояния в другие. Чтобы решить данную систему дифференциальных уравнений нужно задать начальное распределение вероятностей p1(0), р2(0), …рn(0), сумма которых равна единице 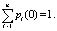
Исследование задачи
С учетом приведенных выше пояснений рассмотрим СМО на примере железнодорожной станции, на которую прибывают поезда, являющиеся потоком заявок. Если в момент времени прибытия поезда все пути заняты, то заявка получает отказ и остается не обслуженной. Следует уточнить, что не обслуженная заявка соответствует поезду, ожидающему освобождение железнодорожного пути на семафоре перед станцией.
Модель пригородного перевозочного железнодорожного процесса включает каждую станцию или остановочный пункт (далее – ОП) как отдельную двухканальную СМО с отказами (рис. 1).

Рис. 1. Граф переходов состояний СМО для пригородного перевозочного ж.д. процесса
Здесь: λвход, λвыход – интенсивности пассажиропотока, соответствующие выходящим и входящим пассажирам; μвход, μвыход – интенсивности обслуживания выходящего и входящего пассажиропотока.
В данную модель необходимо включить интенсивности пассажиропотока, перемещаемого между ОП и интенсивности обслуживания при следовании. Тогда общий вид модели пригородного перевозочного железнодорожного процесса будет следующим (рис. 2).
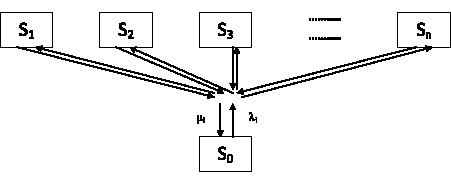
Рис. 2. Обобщенный граф переходов состояний системы
Здесь λi – интенсивность пассажиропотока i-го ОП; μi - интенсивность обслуживания для i-го ОП; Si – состояние системы соответствующих i-му ОП (i = 0, 1, 2 ..., n).
Причем λi = λвыход + λвход + λследования и μi = μвыход + μвход + μследования для i-го ОП. Так как параметры λi и μi находятся в прямой функциональной зависимости – чем больше пассажиропоток, тем большее время потребуется для его обслуживания, то достаточно определение только одного из этих параметров.
Также следует уточнить, что интенсивность пассажиропотока влияет на загруженность вагона и их количество, а то время, которое затрачивается на вход и выход будет определять занятость рассматриваемой СМО обслуживанием. В данном случае время следования между ОП следует исключить из параметров λi и μi, так как его значение может намного превышать значения других параметров суммы, если расстояние между ОП будет большим. Указанный показатель должен учитываться при расчете экономических параметров модели пригородного перевозочного процесса.
Приведем спецификацию модели пригородного перевозочного процесса на основе графа рис. 2.
В соответствии с (2):
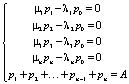 (3)
(3)
Здесь: А – верхняя граница интерактивно задаваемого масштаба, например А = 100.
Система уравнений (3), решаемая методами Гаусса, предназначена для количественной оценки нахождения моделируемой СМО в соответствующем состоянии. Ключевая гипотеза, рассматриваемая в данной постановке – чем больше времени СМО i-го ОП занята обслуживанием пассажиропотока, тем выше вероятность нахождения СМО в рассматриваемом состоянии. По результатам статистических наблюдений количества пассажиропотока можно построить функцию распределения и проводить моделирование с ее помощью. В рамках данной работы ограничимся минимальным и максимальным значением времени обслуживания на i-ом ОП и в рассматриваемом диапазоне определим случайным образом несколько значений для оценки параметров нескольких вариантов модели СМО. Для каждого из определенных значений рассчитаем в соответствии с (3) новые значения рi. Данная процедура нобходима для более точного определения узловых станций и должна проводится за несколько итераций, результаты которых поступают на дальнейшую обработку.
Рассчитанные значения рi по каждой итерации становятся коэффициентами целевой функции следующей задачи линейного программирования (ЛП) [5]:
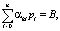
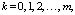 (4)
(4)
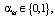
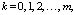 (5)
(5)
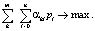 (6)
(6)
Здесь: B – количество ОП на которых моделируется положение узловой станции, например – станция отправления и назначения; α – неизвестные задачи ЛП.
Таким образом, сформулированная задача (4) – (6) сводится к нормальной задаче булевого программирования с n неизвестными переменными и n ограничениями-неравенствами. Для ее решения могут быть использованы, например, методы Гомори или ветвей и границ.
По результатам расчета если i-ый ОП имеет наибольшее количество распределенных значений «1», то он рассматривается как станция отправления или назначения. Также необходимо анализировать дисперсию результатов распределения по ОП. Если распределение носит неодназначный характер, то дополнительно следует учитывать следующие факторы: статус пункта остановки (станция или ОП); возможность отстоя пригородного поезда на период до 12 часов (например в случае прибытия вечером и отстоя до утра).
Для преобразования задачи (4) – (6) к задаче целочисленного программирования ограничение (5) следует модифицировать, следующим образом:
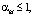
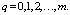 (7)
(7)
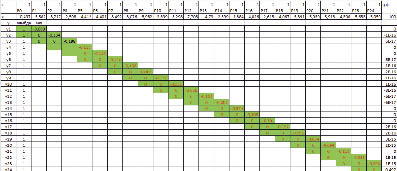
Рис. 3
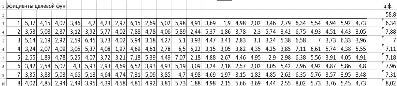
Рис. 4
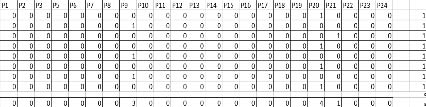
Рис. 5
Пример моделирования пассажирских перевозок
Пусть имеется данные о пассажиропотоке. На основе параметров вагонов, высоте платформы ОП, количестве вагонов пригородного поезда и других данных рассчитывается время на обслуживание пассажиропотока. Далее решается задача (3), общий вид которой представлен на рис. 3. Затем, используя метод решения системы линейных уравнений, определяются неизвестные рi. Результаты расчета восьми вариантов решения задачи (3) представлены на рис. 4. Далее, в соответствии с алгоритмической схемой, решается задача ЛП (4) – (6), где: αki – неизвестные задачи ЛП; рi – коэффициенты целевой функции, определенные в результате многократного решения задачи (3); B = 1 – количество ОП, на которых моделируется положение узловой станции. По результатам расчета (рис. 5) следует, что узловыми станциями необходимо считать ОП, соответствующие S9 и S20. Изменяя параметр B, можно получать различные варианты местоположения узловых станций с учетом приведенных условий постановки задачи. Введение производственных функций в задачу (4) – (6) позволит определить оптимальные маршруты следования пригородных поездов, снизить технические, материальные и трудовые издержки пригородной компании.
Заключение
Полученные результаты позволят своевременно реагировать на нештатные ситуации посредством принятия определенных управленческих решений в следующих случаях:
– при прогнозировании показателей пассажиропотока и времени его обслуживания в пригородных перевозках железнодорожным транспортом;
– на основе данных прогноза определять требуемое количество вагонов пригородного поезда и станции отправления и назначения.
Разработанные модели могут быть использованы в дальнейшем для определения рентабельности пригородных перевозок, снижения ресурсных издержек, повышения эффективности функционирования всего железнодорожного комплекса.

