Среди современных инфотелекоммуникационных технологий наиболее динамичное развитие показывает цифровая обработка сигналов (ЦОС). Цифровая обработка сигналов позволяет относительно легко обеспечить необходимую помехоустойчивость системы обработки сигналов, простое сопряжение, стабильность параметров тракта обработки данных и ряд других преимуществ [1, 2]. Однако при этом, к алгоритмам и метода ЦОС предъявляются довольно высокие требования по производительности. Это приводит к повышенному интересу по использованию непозиционных систем классов вычетов, в частности системы остаточных классов (СОК). Обработка малоразрядных остатков по независимым параллельным вычислительным каналам позволяет не только повысить скорость, но и обеспечить требуемые значения точности конечных результатов. Однако увеличение числа информационных оснований негативно сказывается на аппаратурных затратах вычислительного устройства. Особенно это хорошо видно при выполнении обратного преобразования из модулярного кода в позиционный код. Решить эту проблему можно за счет разработки устройства осуществляющего масштабирование непозиционного кода до необходимой точности. Поэтому разработка устройства масштабирования модулярного кода является актуальной задачей.
Среди систем обработки и передачи данных, реализующих цифровую обработку сигналов, особое место занимают цифровые фильтры (ЦФ). Цифровые фильтры нашли широкое применение в средствах связи, в частности, в блоках предварительной обработки, представляющих собой блоки защиты от помех и в блоках цифровой обработки сигналов. При этом цифровая фильтрация в средствах связи может быть реализована как традиционными цифровыми фильтрами, так и адаптивными ЦФ, в котором традиционный цифровой фильтр является составным элементом этого адаптивного устройства [3–5].
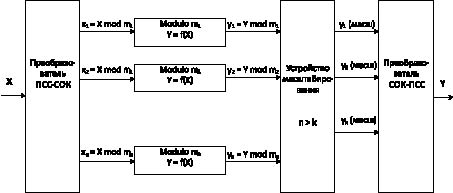
Рис. 1. Непозиционный цифровой фильтр класса вычетов
Развитие теории адаптивной обработки сигналов всегда было непрерывно связано с практикой. Примерами широко используемых на практике адаптивных устройств являются компенсаторы сигналов акустического и электрического эха, эквалайзеры (выравниватели) характеристик электрических и акустических каналов связи, адаптивные антенные и акустические решетки. Эти устройства являются неотъемлемыми элементами оборудования современных радиотехнических систем и систем связи, тактико-технические характеристики, которых часто недостижимы без использования адаптивной обработки сигналов. Сегодняшние практические результаты адаптивной обработки сигналов во многом обусловлены достижениями в цифровой электронике и микроэлектронике, позволившими создавать высокопроизводительные и компактные цифровые устройства на базе СБИС программируемых логических матриц и цифровых процессоров обработки сигналов. Эти устройства обеспечивают реализацию сложных алгоритмов ЦОС в реальном масштабе времени, т.е. на требуемой частоте дискретизации обрабатываемых сигналов [3].
В основе большинства адаптивных устройств находится адаптивный фильтр. Фильтрация сигналов, включая адаптивную фильтрацию, может выполняться как аналоговым, так и цифровым способом. Сегодня в различных устройствах в основном используются цифровые адаптивные фильтры. Подобно фильтрам с фиксированными коэффициентами, существуют две основные структуры адаптивных фильтров. Это фильтры с конечной импульсной характеристикой (КИХ), и фильтры с бесконечной импульсной характеристикой (БИХ), или рекурсивные фильтры [3–5]. Однако практическая реализация цифровых фильтров выявила ряд недостатков, среди которых можно выделить следующие:
– относительно низкая скорость получения отклика фильтра, так алгоритм подстройки коэффициентов фильтра, требует большого количества итераций;
– большие аппаратурные и энергетические затраты при его реализации на существующей элементной базе, которые задаются порядком цифрового фильтра.
Одним из наиболее перспективных путей решения отмеченных выше проблем является использование алгебраической системы, обладающей свойством кольца и поля. Это позволит осуществить реализацию алгоритма цифровой фильтрации в модулярных кодах класса вычетов. В работах [6–10] показаны основные подходы к построению параллельных непозиционных спецпроцессоров. Особое место среди таких реализаций занимают вычислительные устройства ЦОС, функционирующие в системе остаточных классов. Это обусловлено тем, что применение СОК позволяет обеспечить повышение быстродействия, точность и отказоустойчивость работы устройств ЦОС, в том числе и ЦФ по сравнению с позиционной (двоичной) системой счисления [8–10].
Входными сигналами для традиционных и модулярных ЦФ являются сигналы, поступающие с выхода аналого-цифрового преобразователя. На сегодняшний день разрядность входных сигналов ЦФ составляет от 6 до 24 двоичных разрядов [3–5]. Общая структурная схема цифрового фильтра, функционирующего в системе остаточных классов, приведена на рис. 1.
Количество вычислительных каналов фильтра, которые реализуют базовую операцию «сумма парных произведений», задается диапазонов входных и выходных данных. Для получения правильного результата необходимо, чтобы Dсок – диапазон представления данных в модулярном коде был больше диапазона Dпсс, который задает разрядность представления в позиционном коде.
Для выполнения процедур цифровой фильтрации в модулярном коде необходимо осуществить преобразование из позиционной системы счисления (ПСС) в систему остаточных классов. Данную задачу в ЦФ СОК решает прямой преобразователь ПСС-СОК. Для обратного преобразования используют преобразователь СОК-ПСС. Данные преобразователи являются обязательными элементами любого вычислительного устройства, функционирующего в системе остаточных классов.
Чтобы обеспечить минимальные аппаратурные затраты на выполнение обратного преобразования в состав цифрового фильтра введено устройство масштабирования. Оно предназначено для уменьшения динамического диапазона полученного результата до заданной разрядности ЦФ. Рассмотрим пример работы такого устройства на примере 16-разрядного цифрового фильтра, функционирующего в СОК.
Так как диапазон позиционного кода равен Dпсс = 65536, то для выполнения цифровой фильтрации с использованием модулярного кода были выбраны основания СОК m1 = 2, m2 = 5, m3 = 7, m4 = 11, m5 = 13, m6 = 19. Известно, что при умножении двух чисел происходит увеличение диапазона представления результат в 2 раза. Тогда в рассматриваемом непозиционном цифровом фильтре необходимо обеспечить диапазон равный 32 двоичным разрядам. Для выполнения этого условия приведем расширение системы СОК на основания mn+1 = 23, mт+2 = 29, mn+3 = 31, mn+4 = mn+k = 37. При этом модуль m9 = 31 введен с целью исключения переполнения разрядной сетки, которое состоит в выходе за пределы диапазонов представления данных. Тогда расширенная система модулей СОК
m1 = 2, m2 = 5, m3 = 7, m4 = 11, m5 = 13, m6 = 19, m7 = 23, m8 = 29, m9 = 31, m10 = 37.
Введение дополнительных оснований приводит к значительным увеличениям аппаратурных затрат на реализацию обратного преобразователя СОК-ПСС. Чтобы снизить проведем процедуру масштабирования, которая заключается в делении, полученного результата в каждом вычислительном канале на масштабирующий коэффициент Dм, который определяется как
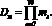(1)
Однако операция деления в СОК не определена. Поэтому был разработан следующий алгоритм масштабирования, представляющий последовательность модульных операций. Масштабирование проводится последовательно, начиная со старшего основания, заканчивая младшим, дополнительно введенным модулем СОК. Для этого необходимо на первой итерации из всех оставшихся остатков αi(1), i = 1,…,9 вычесть значение старшего остатка α10(1). Затем полученный результат умножается на величину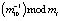 
. В результате произведено масштабирование на величину старшего основания СОК. Данная операция продолжается до тех пор, пока не останутся основания, определяющие размерность входных данных ЦФ. В общем виде операция масштабирования в ЦФ СОК задается выражением
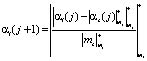, (2)
где j – номер итерации масштабирования.
На рис. 2 представлена структура устройства масштабирования цифрового фильтра, функционирующего в СОК. Устройство содержит регистры (RG) для хранения промежуточных результатов по модулям mi, где i = 1,…,9, прямые преобразователи (FC) по модулю mi, сумматоры ADD по модулю mi, умножители MLP на величину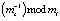 
, мультиплексор MUX. При этом вторые выходы первых шести регистров подключены к входам обратного преобразователя СОК-ПСС. Рассмотрим его работу.
Пусть на вход устройства масштабирования подается А = (1,3,1,1,11,5,2,13,20,36), что соответствует числу А = 154867134. Старший остаток α10(1) = 36 через мультиплексор MUX подается на входы преобразователей FC1 – FC9, с выходов которых снимется значение остатка по модулю m1 – m9 соответственно. Тогда разность числа А и вычисленных остатков будет равна А = (1, 2, 0, 9, 1, 7, 12, 6, 15, 0). Полученные остатки поступают на входы умножителей MLP1 – MLP9, где умножаются на константу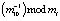 
соответственно. В результате получаем А(1) = (1, 1, 0, 5, 6, 12, 14, 8, 18). Полученный результат соответствует масштабированию на величину m10 = 37.
По оставшимся модулям m = 23, m = 29, m = 31 итерации масштабирования выполняются аналогичным образом. В результате будет получен код системы остаточных классов А(4) = (0, 3, 1, 8, 6, 12). Это соответствует числу 6168. В рассмотренном примере было проведено масштабирование с коэффициентом Кмасш = 765049. При проведении масштабирования исходного числа А, представленного в ПСС, на данную величину будет получен результат 6168,7. Таким образом, ошибка масштабирования составит δ = 0,01 %. Следовательно, разработанное устройство масштабирования в модулярном коде позволяет получить достаточно точный результат при меньших схемных затратах при реализации цифрового фильтра.
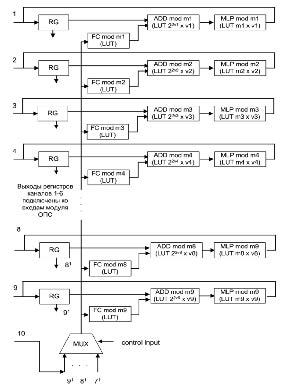
Рис. 2. Структура устройства масштабирования
Выводы
Применение модулярных кодов системы остаточных классов позволяют обеспечить цифровую фильтрацию сигналов в реальном масштабе времени за счет использования малоразрядных вычислительных трактов. При этом для достижения высокой точности результатов используются дополнительные основания СОК, что негативно сказывается на аппаратурных затратах, особенно при проведении обратного преобразования из модулярного кода в позиционный код. Разработанное устройство масштабирования позволяет снизить эти затраты за счет уменьшения числа основания, используемых при обратном преобразовании СОК-ПСС. При этом ошибка масштабирования составит величину δ = 0,01 %. Полученный результат свидетельствует о достаточно высокой эффективности разработанного устройства масштабирования для непозиционного цифрового фильтра.