В Росси с 1 января 2016 года в силу вступает новый криптографический стандарт ГОСТ Р 34.12-2015 «Информационная технология. Криптографическая защита информации. Блочные шифры» [3]. В его состав вошли два алгоритма шифрования. Одним из них является действующий стандарт шифрования ГОСТ 29147-89, для которого зафиксированы блоками замены. В новом стандарте данный шифр фигурирует под названием Магма [4]. Магама представляет собой симметричный блочный шифр с размером блока данных 64 бита, секретным ключом 256 бит и 32 раундами шифрования. Подробнее о работе алгоритма шифрования Магма можно прочесть в [1, 3].
В настоящей работе впервые представлены результаты по разработке и реализации параллельных алгоритмов шифрования данных с использованием технологии Cuda, которые будут использованы в дальнейшем для проведения экспериментов по оценке стойкости шифра Магама с использованием различных методов криптоанализа. Cuda представляет собой программно-аппаратную архитектуру, призванную увеличить производительность вычислений при помощи использования графических процессоров NVIDIA. В основе ее архитектуры лежит язык программирования С с небольшими видоизменениями [4]. Данная технология применятся в тех случаях, когда есть необходимость в параллельном выполнении одинаковых операций (вычислений). Не обошла стороной эта архитектура и криптографию. CUDA и подобные ей GPGPU как ничто другое подходят для параллельного вычисления в блочных шифрах [1, 4]. В данной статье мы рассмотрим применимость данной технологии к криптографическому алгоритму Магма. Выбор данной технологии обусловлен большим запасом вычислительной мощности, доступностью и относительной простотой реализации, а также возможностью моделировать процесс в условиях лаборатории.
Технология Cuda применима для параллельного вычисления блоков.
Принципы распараллеливания, представленные на рис. 1 в нашем алгоритме реализованы следующим образом. Для параллельного вычисления здесь будем использовать следующие параметры: N – количество блоков, th – количество потоков. Если заявленное количество блоков меньше количества потоков, то вызов кода на GPU выполняется с N потоками, в обратном же случае исходный массив текста делится по th блоков и для каждого из новых массивов вызывается функция GPU. Суть данной функции состоит, как указано выше, в шифровании одного блока 32-раундами. Для обращения к отдельным блоком используется стандартный идентификатор потока [2].
Рассмотрим работу данного алгоритма на примерах из кода.
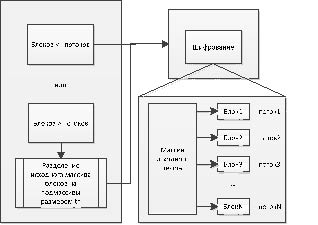
Рис. 1. Общая схема распараллеливания
Таблица 1
Экспериментальные данные для параллельной реализации алгоритма Магма с использованием технологии Cuda (на 1 мбит шифрования в зависимости от потоков)
|
Потоков |
Мсек |
Итераций |
|
1 |
8580 |
15625 |
|
10 |
8556 |
1563 |
|
20 |
8477 |
782 |
|
50 |
8737 |
313 |
|
100 |
9034 |
157 |
|
192 |
8736 |
82 |
|
500 |
10983 |
32 |
|
1000 |
4214 |
16 |
|
1024 |
4504 |
16 |
|
2000 |
4338 |
8 |
|
5000 |
5301 |
4 |
|
7000 |
5636 |
3 |
|
10000 |
5256 |
2 |
|
12000 |
6623 |
2 |
|
15625 |
37 |
1 |
int blocks[N]; непосредственно массив блоков исходного текста;
int *dev_block; копия исходного массива для работы на девайсе;
int size = N * sizeof(int);
cudaMalloc( (void**)&dev_block, size ); выделяем память на девайсе
cudaMemcpy(dev_block, blocks, size, cudaMemcpyHostToDevice); копируем данные на девайс
block_enc <<< 1, N>>>(dev_block); запускаем функцию block_enc на GPU, передавая ей параметры N – количество потоков(данный код взят из участка, где N<th), dev_block – массив блоков.
Как видно из примера, передать функцию на GPU не составляет особого труда. Рассмотрим внутреннюю организацию функции и отдельно остановимся на нюансах реализации.
__global__ void block_enc(int *blocks)
{
/…/
int LE = blocks[threadIdx.x] >> 32;
int RE = blocks[threadIdx.x] & 0xffffffff;
На продемонстрированном выше участке кода используется threadIdx.x – встроенная переменная, используемая для доступа к отдельной нити. Это необходимо для параллельного расчета отдельных блоков.
Далее происходит обычное шифрование, просчитываются 32 цикла, реализация аналогична реализации на CPU.
Тестирование программы производилось на видеокарте NVIDIA GTS 450, Intel Core i5 2400, 8 Gb RAM. По замерам времени на шифрование 1 мбит информации были получены результаты, представленные в табл. 1. По полученным результатам был построен график, приведенный на рис. 2. Проанализируем полученные результаты. На графике (рис. 2) отчетливо видны резкие скачки, и естественно возникает вопрос, чем они обусловлены. Почему, например, на 500 потоках шифрование данных осуществляется дольше, чем на 100 или 192, а на 12000 – дольше, чем на 1024 и 2000. Для ответа на этот вопрос обратимся к работе [5]: «/…/ для небольшого количества блоков правильный выбор числа потоков весьма важен, производительность скачет на 15–20 %. Для чтения по строкам, изменение количества блоков не влияет на выравнивание: каждый блок обрабатывает целое количество строк (и это количество между блоками не различается более чем на 1), а строки выровнены на 16 килобайт. В то же время, количество блоков, некратное числу исполняющих мультипроцессоров приведет к частичному простою мультипроцессоров». Таким образом, можно сделать вывод о том, что данные скачки вполне естественны, и при грамотном выборе количества потоков можно достичь максимально эффективных результатов. Не стоит также забывать о том, что при условии N > th разбиение на массивы меньшего размера происходит непосредственно на CPU, что также занимает определенное количество времени.
Для оценки эффективности разработанного алгоритма предварительно проводились замеры на CPU Intel Core i5 3210M 8Gb RAM без использования параллельных вычислений. Шифрование 1 блока информации (64 бита) заняло меньше мсек, когда как на видеокарте на это ушло 30–40 мсек. Для шифрование 1 мбита на процессоре понадобилось порядка 40-50 мсек. На видеокарте результат аналогичен предыдущему – 37 мсек. Но на больших массивах данных (тест проводился на 100000 блоках = 6.4 мбит) расчет на CPU составил 868 мсек, когда на GPU шифрование этих же данных заняло около 40 мсек. Реультаты экспериментов сведены в табл. 2.
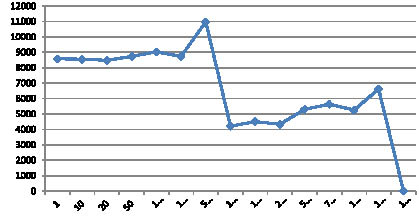
Рис. 2. График зависимости времени шифрования(мс) от числа потоков
Таблица 2
Экспериментальные данные шифрования алгоритмом Магма на CPU без распараллеливания
|
Блоков |
Мсек |
|
1 |
0 |
|
500 |
6 |
|
1000 |
10 |
|
5000 |
55 |
|
10000 |
99 |
|
12000 |
115 |
|
15625 |
140 |
|
50000 |
455 |
|
100000 |
868 |
Зависимость времени выполнения от количества блоков приведена на рис. 3. Также производились замеры шифрования с использованием не только GPU-потоков, но и GPU-блоков в соответствии с моделью, представленной на рис. 4.
Результаты экспериментов для GPU-блоков (в соответствии с рис. 4) получились аналогичными вычислениям на потоках. Шифрование на 25 блоках и 625 потоках заняло время, равное шифрованию на 1 блоке и 15625 потоках, что закономерно.
В соответствии с данными сравнения CPU и GPU (рис. 5), взятыми с официального сайта NVIDIA [6], прирост производительности вычислений на GPU относительно CPU разумнее выполнять на больших объемах данных, тогда как на малых объемах они могут оказаться даже медленнее, чем на процессоре. Это подтверждается результатами экспериментов, проведенных с помощью разработанного и реализованного алгоритма, которые были представлены выше.
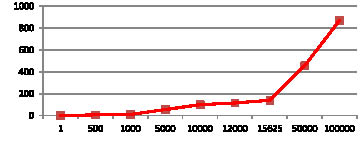
Рис. 3. Зависимость времени шифрования на CPU от количества блоков исходного текста
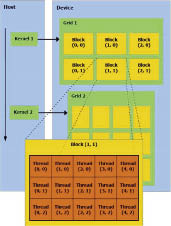
Рис. 4. Блочно-поточная модель GPU
Рис. 5. Сравнение CPU и GPU (с оф.сайта NVIDIA)
Не стоит забывать, что на приведенных выше примерах разделение исходного текста на блоки для посылки на GPU происходило на CPU, что занимало бы время на больших объемах информации. Данную процедуру можно было бы произвести на видеокарте, но это потребовало бы больших ресурсов памяти.
Разработанный и реализованный алгоритм на практике подтверждает эффективность применения параллельных вычислений для ускорения процесса шифрования данных. Это может быть использовано в дальнейшем, для проведения различных исследований в области надежности шифра Магма с применением различных методов анализа, с целью сокращения общего времени, затрачиваемого на исследование шифра.
Работа выполнена при поддержке гранта РФФИ № 15-37-20007-мол-а-вед.

