Контролю износа оборудования, определению сроков ремонта уделяется большое внимание, разрабатываются методы, готовятся специалисты. Как правило, в паспорте или инструкции к устройству указываются пределы допустимых нагрузок, различные предупреждения и т.п. Они формулируются в результате изучения работы именно этого устройства. Для других систем вопросы безопасности необходимо ставить и решать заново. А существует ли универсальный подход к диагностике?
В последние годы появились предложения предсказывать аварии [1] (и, более широко, предвидеть будущее [2]) с помощью метода compressive sensing [3]. Предполагается, что система подчиняется некоторым уравнениям, но уравнения эти неизвестны. Их реконструкция осуществляется с помощью специального кода (компьютерной программы). После того как уравнения установлены, можно получить всю информацию о системе, в частности, условия, при которых данное состояние теряет устойчивость. Однако авторы отмечают трудности: если система сложна, уравнений много, а также из-за того, что исходные данные искажаются неизбежным шумом.
Мы предлагаем другой метод предсказания аварий, оценки износа оборудования, свободный от этих недостатков (см. [4]). Оказалось, что именно шум предупреждает о приближении катастрофы. Поясним, на чем основан такой вывод.
Прежде всего, введем понятие об установившихся режимах. Если система взаимодействует только с окружающей средой, то через некоторое время (время релаксации) она приходит в равновесие со средой. Равновесие зависит только от среды и не зависит от начального состояния системы. Пусть теперь система подвергается внешнему воздействию (питание, накачка). Через время порядка времени релаксации зависимость от начальных условий исчезает (они «забываются»). Формируется установившийся режим, один и тот же для целого набора начальных условий. Режим устойчив: отклонение вызывает «силу», которая возвращает систему в прежнее состояние. Однако вблизи границы устойчивости возвращающая сила уменьшается, релаксация замедляется.
Когда внешнее воздействие не зависит от времени, среди установившихся режимов могут быть стационарные. В дальнейшем, будем, в основном, рассматривать только такие режимы. Равновесие есть предельный случай стационарного режима, когда интенсивность накачки стремится к нулю. Пусть теперь кроме постоянного воздействия есть еще возмущающая переменная сила s sin at, s – малая амплитуда, о – частота. Такая добавка вызовет небольшие отклонения с той же частотой. Чем ниже частота, тем больше отклонение, которое успевает произойти, прежде чем направление воздействия изменится. Таким образом, отклик системы на малое возмущение усиливается по мере приближения к границе устойчивости и понижения частоты возмущения.
В реальности, малые возмущения присутствуют всегда, но они не имеют вид синусоиды, а представляют собой случайную функцию времени или, как говорят, шум. В равновесии это тепловые флуктуации, броуновское движение. Вдали от равновесия обычно имеется сторонний шум (например, случайные колебания напряжения в сети). Интенсивность такого шума, как правило, больше, чем у теплового. В критической области, вблизи границы устойчивости, или, как говорят математики, вблизи бифуркации, шум усиливается. Из сказанного выше об отклике ясно, что в наибольшей степени усиливаются низкочастотные составляющие, так называемые мягкие моды.
Если к оборудованию подсоединить датчик, воспринимающий шум, а сигнал от датчика через амплитудно-цифровую плату передавать на компьютер, выполняющий спектральное разложение (преобразование Фурье), можно по нарастанию мягких мод заранее узнать о приближении аварии и принять необходимые меры. Важнейшее свойство такого метода – его универсальность. Он применим к любым видам промышленного оборудования, а также к природным катастрофам (например, критическим явлениям в литосфере, землетрясениям, извержениям вулканов). Описанные свойства критического поведения подобны универсальным законам природы, законам термодинамики.
Представленные соображения не являются общим и строгим доказательством – разнообразие бифуркаций велико. Но мы пока не обнаружили ни одного контр-примера, тогда как нарастание мягких мод перед срывом режима получено и при численном моделировании, и в опытах.
В реальных опытах всегда получается некоторый разброс результатов (ошибки измерений). При численном моделировании, чтобы приблизиться к экспериментальной ситуации, в уравнения вводился слабый случайный источник, так что они превращались в уравнения Ланжевена. По своим статистическим свойствам источник представлял собой белый шум. В реальных системах шум не обязательно белый. Однако вблизи бифуркации корреляционное время критических пульсаций растет и заведомо превышает корреляционное время шума. На таком фоне любой шум выглядит как S-коррелированный (белый). На рис. 1 показан пример частотного спектра автоволны (бегущего фронта) вблизи порога распространения.
Наряду с численным моделированием, были проведены опыты с нелинейной электронной схемой. Рабочим элементом схемы служил динистор. Вольтамперная характеристика этого прибора имеет три ветви: ветви слабого и сильного тока, а между ними – промежуточную, неустойчивую. Шумовое воздействие обеспечивали колебания в источнике питания. Последовательно с динистором было включено постоянное сопротивление. Меняя его величину (или приложенное напряжение) можно было сдвигать точку пересечения характеристики и нагрузочной прямой.
На рис. 2 представлены два спектра. Верхний получен, когда такое пересечение имело место вблизи бифуркации, скачка с нижней ветви на верхнюю. Нижний спектр отвечает пересечению вдали от этой критической точки.
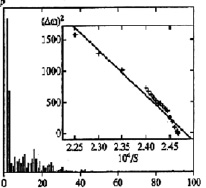
Рис. 1. Спектр бегущего фронта. На врезке – зависимость полуширины низкочастотного пика от расстояния до порога
Как видим, нижний график не имеет никаких особенностей, похож на белый шум, тогда как у верхнего виден низкочастотный пик – своего рода резонанс на нулевой частоте. Обратим внимание на логарифмический масштаб оси ординат, высота пика над фоном составляет несколько порядков.
Нижний спектр отвечает пересечению вдали от этой критической точки. Как видим, нижний график не имеет никаких особенностей, похож на белый шум, тогда как у верхнего виден низкочастотный пик – своего рода резонанс на нулевой частоте. Обратим внимание на логарифмический масштаб оси ординат, высота пика над фоном составляет несколько порядков.
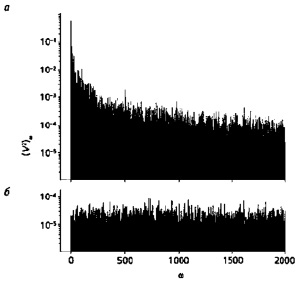
Рис. 2. Частотные спектры электронной схемы с динистором. Частота связана с номером n соотношением ои = 2лп/tm, tm = 100 s – время измерения
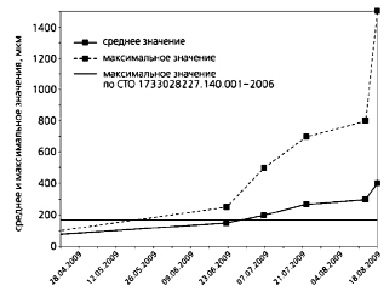
Рис. 3. Зависимость средней и максимальной амплитуд вибраций крышки подшипника
После аварии на Саяно-Шушенской ГЭС появилась статья [5], в которой подробно рассматривались поставленные ею научно-технические вопросы. Однако внимание авторов не привлек акт Ростехнадзора, который несколько дней был доступен на сайте этого ведомства. В акте имеется лишь один график: (рис. 3) зависимость средней и максимальной амплитуд вибраций крышки подшипника турбины (см. [6]). Крышка была сорвана, в машинный зал хлынула вода, погибли люди.
За время наблюдений (свыше 4 мес.) среднее значение амплитуды возросло в 3 раза, а максимальное – в 15 раз. Отмечается, что резонансов обнаружено не было. Значит, единственной причиной такого различия среднего и максимума является сжатие спектра, резонанс на нулевой частоте. Горизонтальная линия на графике показывает границу допустимых значений амплитуды, полученную, по-видимому, традиционными методами. Отличие средней амплитуды от этой горизонтали относительно невелико. Так как граница безопасности проводится обычно с некоторым запасом, можно предположить, что катастрофы удалось бы избежать, если бы не нарастание мягких мод. Слежение за частотным спектром не было предусмотрено системой безопасности. Поэтому о нарастании можно судить лишь по косвенным признакам, как это описано выше. Кроме лабораторных опытов, желательно провести исследования на действующем оборудовании. Разумеется, никто не позволит экспериментировать с трансформаторной подстанцией или авиационным двигателем – на предмет приближения к катастрофе! Остается возможность провести измерения на устройстве, подлежащем ремонту, до и после ремонта. В качестве такого устройства была выбрана автомашина Института, выполнены измерения вибраций подвески, записан частотный спектр. Источником стороннего шума служил двигатель, работавший вхолостую. Предполагалось после ремонта провести такие же измерения. Однако руководство Института отказалось от ремонта, решило машину списать. Поэтому программа работы была изменена: новые измерения провели на четырех машинах, не подлежащих ремонту. На рис. 4 показан низкочастотный край спектра для всех пяти машин. Видно, что низкочастотный пик получен только для машины, подлежащей ремонту.
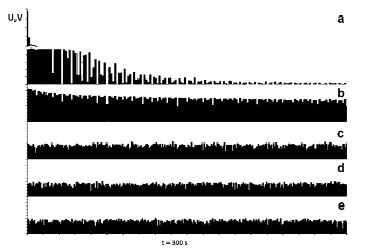
Рис. 4. Частотные спектры вибраций подвески для пяти легковых автомобилей при холостом ходе двигателя. Частота ои = 2т /10, время измерения t0 = 300 s
У остальных вибрации подвески либо вообще не имеют пиков, либо это слабые резонансы, удаленные от низкочастотного края.
Заключение
У полупроводниковых приборов и ряда других систем наблюдается так называемый фликкер-шум, интенсивность которого обратно пропорциональна частоте [6, 7]. В отличие от такого эффекта, рассматриваемый здесь низкочастотный пик появляется только в критических условиях. Его высота растет, а ширина сокращается по мере приближения к границе устойчивости режима. Рост ограничивает только нелинейность воздействия. При удалении от границы пик исчезает.
Еще раз подчеркнем: мы не предлагаем отменить существующие привычные методы диагностики. Новый метод – это дополнение к тому, чем уже располагают инженеры и технологи.

