В статье «Вращение взвешенного шара в неоднородном потоке жидкости» [2] получены формулы для компонентов скорости жидкости в сферических координатах при условии, что шар радиуса а увлекается потоком жидкости и им же приводится во вращение:
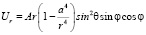 ;
;
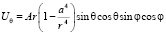 ; (1)
; (1)
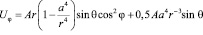 ,
,
где 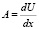 –
градиент скорости, когда нет шара; a – радиус шара, ?, r, ? –
сферические координаты. Предполагается, что жидкость течет вдоль оси y
и вдали от шара ее скорость определяется формулой
–
градиент скорости, когда нет шара; a – радиус шара, ?, r, ? –
сферические координаты. Предполагается, что жидкость течет вдоль оси y
и вдали от шара ее скорость определяется формулой 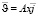 .
.
Для определения влияния шара на вязкость жидкостей необходимо определить тензор напряжений и поток энергии через сферу радиуса R»a. Тензор напряжений в сферических координатах представляется в виде:
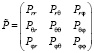 .
.
Плотность потока энергии определяется произведением:
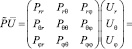
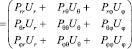 .
.
Верхняя строчка результирующего вектора есть радиальная составляющая вектора плотности потока энергии:
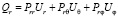 . (2)
. (2)
Необходимые компоненты тензора напряжений определяются по формулам согласно [3]:
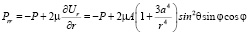 ;
;
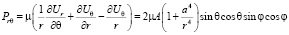 ; (3)
; (3)
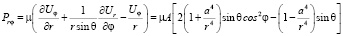 .
.
Подставляя эти компоненты в (2), получаем:
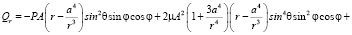
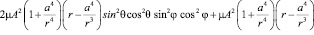
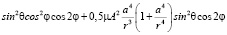 . (4)
. (4)
Зная вектор плотности потока энергии нетрудно определить поток энергии через сферу радиуса R.
Так как
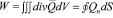 , то
, то
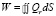 , где
, где 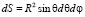 . (5)
. (5)
Поскольку 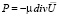 [2], то
[2], то
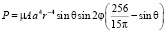 . (6)
. (6)
Учитывая значение 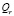 ,
подставим (4) и (6) в (5) и проинтегрируем по ?
и ?. После взятия соответствующих интегралов и приведения
подобных членов получим:
,
подставим (4) и (6) в (5) и проинтегрируем по ?
и ?. После взятия соответствующих интегралов и приведения
подобных членов получим:
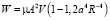 , (7)
, (7)
где 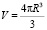 – объем того шара, по поверхности которого проводилось интегрирование, R – его радиус.
– объем того шара, по поверхности которого проводилось интегрирование, R – его радиус.
Полученный результат говорит о том, что при данной постановке задачи шары радиуса «а» не увеличивают вязкость жидкости, а уменьшают. Шары, приводящиеся в движение жидкостью, способствуют скольжению одного слоя жидкости по поверхности другого. Об этом говорит знак «-» в формуле (7), где первое слагаемое – это выделяемая энергия жидкостью в отсутствии шаров.
Этот вывод соответствует тому случаю, когда шары не участвуют в тепловом вращательном движении.
Тепловая угловая скорость вращения кластеров определяется из соотношения:
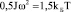 .
.
Моделируя кластер шаром радиуса а можно получить ?:
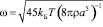 . (8)
. (8)
Если предположить, что в кластере находится n = 125 молекул и что его плотность равна плотности жидкости, например воды, получаем:
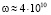 c-1.
c-1.
Реальный градиент скорости течения жидкости составляет порядка 100с-1. Даже если градиент скорости будет 103 с-1, угловая скорость кластера, индуцированная течением, составит всего 500 с-1. Отсюда понятно, что механизм передачи импульса, предложенный в [1] не может работать. Угол поворота кластера в индуцированном движении за один оборот теплового движения составит всего ~0,0211. Далее, кластеры в жидкости имеют самые различные размеры. Поэтому имеет смысл говорить лишь о среднем размере кластера, который следует положить постоянным. При хаотическом движении молекул и кластеров при тепловом равновесии угловая скорость кластеров имеет произвольное направление; скорости образования кластеров и их распада равны. По этой причине, сколько кластеров будет тормозить движение жидкости, столько же будет способствовать движению, имея противоположное вращение.
Из сказанного следует, что вращательное движение кластеров не может влиять на вязкость жидкостей тем механизмом, который описан в [1]. Тепловое вращательное движение тормозится жидкостью, но оно никак не связано с макроскопической скоростью течения жидкости. Более того, ниже покажем, что тепловое вращательное движение тормозится очень мало.
У А. Эйнштейна в [4] получена формула для среднеквадратичного отклонения какого-либо параметра при хаотическом движении молекул:
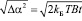 , (9)
, (9)
где kБ – постоянная Больцмана; Т – абсолютная температура; В – подвижность системы по отношению к исследуемому параметру ?; t – время, в течение которого происходит изменение данного параметра.
Так, если исследуется перемещение броуновской частицы за время t,
то параметр В определяется из следующих соображений. Под действием силы
F и силы сопротивления, определяемой по формуле Стока, частица
приобретет скорость 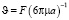 . Следовательно, подвижность этой частицы с радиусом а равна:
. Следовательно, подвижность этой частицы с радиусом а равна:
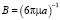
и ее среднеквадратичное отклонение за время t будет:
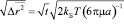 . (10)
. (10)
Применим эти рассуждения к вращательному движению кластеров. Если шар радиуса а вращается в вязкой среде под действием момента М, то он приобретает угловую скорость
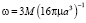 .
.
Значит 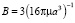 , а среднеквадратичный поворот шара в хаотическом движении будет:
, а среднеквадратичный поворот шара в хаотическом движении будет:
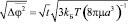 . (11)
. (11)
За одну секунду угловое перемещение описанного выше кластера составит 49300 градусов или 3070 оборотов.
Из сравнения формул (10) и (11) видно, что угловое перемещение кластера сильнее зависит от его размера, чем пространственное перемещение. Отсюда понятно, почему броуновские частицы практически не вращаются. Громадное среднеквадратичное угловое перемещение кластера говорит о том, что он вращается практически свободно. По этой причине вращательное движение кластеров и не влияет на вязкость жидкостей.
На вязкость жидкостей влияет лишь поступательное движение кластеров. Эта задача рассмотрена мной в статье [5]. Там я повторял решение А. Эйнштейна, взятое им у Кирхгофа. Причем там рассматривалось движение жидкости типа радиального. Так А. Эйнштейн моделировал влияние шара. Задача о движении шара в неподвижной вязкой жидкости рассмотрена в [3]. Ниже воспользуемся этим решением.
Пусть жидкость течет вдоль оси z системы координат жестко связанной с шаром радиуса а. В этом случае поле скоростей вокруг шара определяется уравнениями [3, стр. 500]:
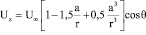 ;
;
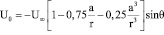 . (12)
. (12)
Давление, обусловленное течением равно:
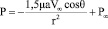 . (13)
. (13)
Определив Prr и Pr?, а затем поток энергии через сферу радиуса R R>>a, получим:
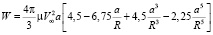 . (14)
. (14)
Учитывая, что 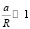 , можно отбросить слагаемые, содержащие a/R.
, можно отбросить слагаемые, содержащие a/R.
Тогда выражение (14) можно упростить:
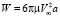 . (15)
. (15)
Формула (15) получается более простым путем, если вспомнить формулу Стокса для силы сопротивления при движении шара в вязкой жидкости:
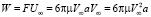 .
.
Пусть теперь шар радиуса а двигается в неоднородном потоке жидкости. Потери энергии жидкости вследствие вязкости в отсутствии шаров получим из (7) при а = 0:
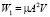 ,
,
где V – объём жидкости, A – градиент скорости.
Поступательное движение шара со скоростью U? создает дополнительные потери энергии
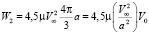 ,
,
где 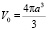 – объём шара.
– объём шара.
Скорость U? – это скорость поступательного движения
кластера, моделируемого шаром радиуса а. Кластер подобно броуновской
частице перескакивает с одного места на другое. Поэтому скорость
движения кластера сравнима с макроскопической скоростью. Отсюда
можно предположить, что 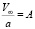 – градиенту макроскопического движения жидкости. Тогда, заменяя
– градиенту макроскопического движения жидкости. Тогда, заменяя 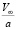 через А и складывая с W1, для W можно записать следующее выражение:
через А и складывая с W1, для W можно записать следующее выражение:
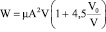 . (16)
. (16)
Остается учесть, что в жидкости находится не один кластер, а много; пусть будет их N. Будем считать, что средний размер кластера не меняется и что они не влияют на поле скоростей вокруг друг друга. В этом случае потери энергии от присутствия каждого кластера будут равны и (16) можно переписать в виде:
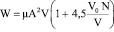 . (17)
. (17)
Сравнивая формулу (17) с 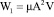 ,
можно считать круглую скобку в (17), как множитель меняющий
вязкость жидкости. Обозначим вязкость кластеризованной жидкости ?K,
а вязкость при отсутствии кластеров через ?0. Тогда имеем:
,
можно считать круглую скобку в (17), как множитель меняющий
вязкость жидкости. Обозначим вязкость кластеризованной жидкости ?K,
а вязкость при отсутствии кластеров через ?0. Тогда имеем:
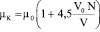 . (18)
. (18)
Из (18) видно, что наличие кластеров в жидкости увеличивает ее вязкость. Объём кластеров V0 и их количество зависят от температуры. Степень кластеризации минимальна при температуре кипения и максимальна в точке плавления.
Формула (18) позволяет объяснить наши опыты по измерению вязкости отстоянной и хорошо перемешанной воды. Во всех опытах получалось, что вязкость воды после перемешивания уменьшалась. Значит, при тщательном перемешивании уменьшался размер кластеров и их число. Хотя это качественное объяснение, но всё таки объяснение.

