Пусть шар радиуса a находится в неоднородном потоке жидкости и двигается вместе с жидкостью. Поскольку шар увлекается жидкостью, то можно считать, что в системе отсчета центра шара скорость этого центра равна нулю. Тогда с одной стороны шара поток жидкости направлен вдоль оси y, а с другой стороны – против оси y (рис. 1). Вследствие малых размеров шара можно считать градиент скорости в масштабах шара малым.
Пусть градиент скорости равен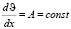 
вдали от шара. В плоскости yoz скорость частиц жидкости равна нулю. В
этом случае невозмущенный поток можно представить равенством:
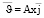. (1)
Следовательно, поле скоростей на бесконечности в сферической системе координат представляется следующим образом:
;
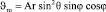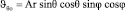; (2)
,
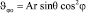где угол ? отсчитывается от оси х, а угол ? – от оси z.
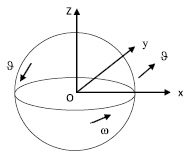
Рис. 1. Картина течения жидкости вокруг шара
Движение жидкости вокруг шара считается стационарным. Тогда уравнения движения жидкости с учетом малости скоростей будут иметь вид:
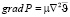; (3)
,
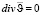где Р – давление в жидкости, ? – коэффициент вязкости жидкости.
Поле скоростей будем искать в виде:
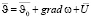. (4)
Здесь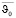 
– скорость на бесконечности, скалярная функция ? и 
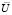описывают возмущения, вносимые шаром, в движение жидкости. Так как 
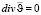и 
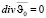, то
.
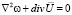Далее, поскольку
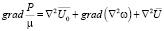
и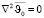 
, а также положим 
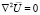, то 
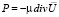и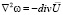 
.
Таким образом, задача свелась к решению уравнений:
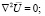(5)
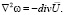(6)
Граничные условия вытекают из предположения, что жидкость прилипает к поверхности шара, т.е.
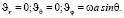(7)
Кроме того, на бесконечности возмущения должны исчезать:
.
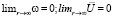Поскольку решается внешняя задача, то общее решение уравнения Лапласа можно записать в виде [2]:
.
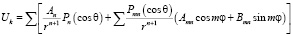Учитывая зависимость ?r и ?? от углов ? и ?, следует положить: r = 2, m = 2, т.е.
;
;
,
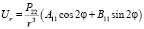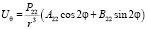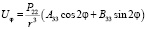где P22 – присоединенный полином Лежандра.
Найдем divU. Учитывая, что
,
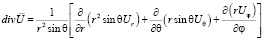получили:
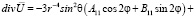
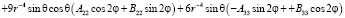. (8)
Здесь учтено, что P22 = 3sin2?.
Теперь необходимо решить уравнение (6) с учетом (8). Это есть уравнение Пуассона, типа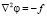 
, решение которого хорошо известно
.
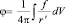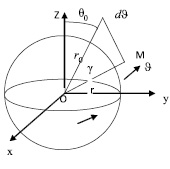
Рис. 2. Расположение точки М и объема dV
Следовательно, решение уравнения (6) находится таким же образом:
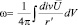, (9)
где 
–
есть расстояние от объема dV до точки наблюдения M (рис. 2). Объем dV
имеет координаты (r0?0?0), а точка M определяется координатами (r,
?, ?). Следовательно,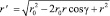 
, где ? – угол между r0 и r.
Следовательно,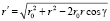 
.
Представим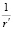 
в виде ряда по полиномам Лежандра:
.
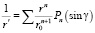Учитывая, что угол ? зависит от координат т. М и объема dV и теорему сложения для полиномов Лежандра, получаем:
.
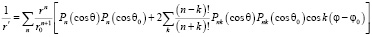Подставляя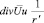 
в уравнение (6), будем иметь:
.
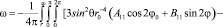
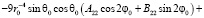
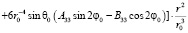
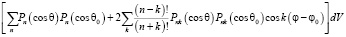Вследствие ортогональности тригонометрических функций интегралы по ? не равны нулю только при k = 2. А при k = 2 имеем:
; 
;
; 
.
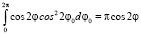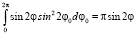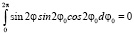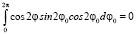После взятия интегралов по ? получаем:
.
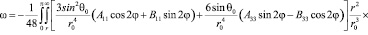
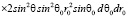Интегрирование по ? дает:
; 
.
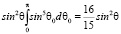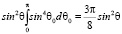Для интегрирования по r точку М выбираем достаточно близко к шару, поскольку возмущения наибольшие вблизи шара. Поэтому и проводится интегрирование по r0 от r до бесконечности. Тогда
.
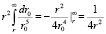Таким образом, окончательно имеем:
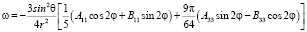. (10)
Подставляя (10) в (4) и используя граничные условия (7), получаем:
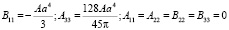. (11)
Отсюда для проекций вектора скорости получаем следующие выражения:
; 
;
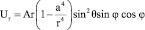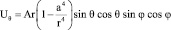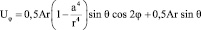или
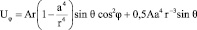. (12)
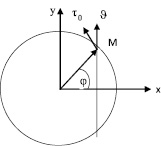
Рис. 3. К определению силы, вращающей шар
Поскольку при r = a U? = ?asin?, то из (12) следует, что угловая скорость вращения шара должна быть 0,5A:
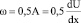. (13)
В статье [1] считается, что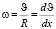 
. Нетрудно понять, что угловая скорость шара была бы такой, если бы жидкость касалась шара только в узкой полосе при 
,
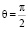а ? = 10 ° – 15 °. Но жидкость ударяется о шар
и при других углах, где скорость жидкости не равна линейной
скорости соответствующих точек поверхности шара.
В точке М касательная скорость равна Аxcos? а не Aa и, следовательно, здесь не жидкость раскручивает шар, а шар движет жидкость. Если найти силу, действующую на шар, то она будет иметь положительное направление до угла 45 °, а после – направлена отрицательно.
Выводы:
1. Взвешенный шар в неоднородном поле скоростей жидкости увлекается жидкостью и вращается вследствие наличия градиента скорости.
2. Угловая скорость вращения шара не равна градиенту скорости жидкости на бесконечности, а составляет половину градиента скорости.
3. Момент сил, действующих на шар со стороны жидкости равен нулю, что обеспечивает его стационарное вращение.
4. Задача будет использована для рассмотрения влияния вращения кластеров на вязкость жидкости.