Совокупность матриц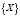 
из 
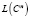предельно диагонализуема, если существует такая последовательность матриц Ap∈GL(Cn), 
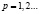, что все матрицы 
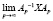являются диагональными для всех X из совокупности. Будем предполагать, что совокупность матриц 
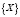образуют алгебру Ли G.
Теорема. Для того чтобы алгебра G была предельно диагонализуемой необходимо и достаточно, чтобы алгебра G была разрешимой.
Доказательство необходимости основано на теореме Леви-Мальцева [1] о разложении алгебры в прямую сумму радикала алгебры и полупростой подалгебры алгебры.
Для доказательства достаточности используется существование базиса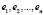 
в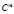 
, в котором все матрицы из G имеют нижнетреугольный вид (теорема Ли). Матрицы 
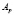вида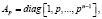 
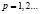, образуют искомую последовательность. Матрицы 
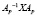представляются в виде
,
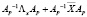где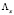 
диагональная матрица, и значит
= 
,
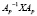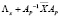матрицы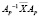 
имеют вид
и при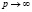 
стремятся к нулевой матрице.