Поиск высший измерений пространства – времени продолжается в астрофизике в течение десятилетий. Эта программа действует на всех крупных ускорителях и обсерваториях космических лучей. Обнаруженные в конце прошлого века осцилляции нейтрино, нобелевская премия за изучение которых вручалась в 2002 и 2015 гг., трактуются сегодня как эффекты в многомерном струнном пространстве. Измерение размерности D этого пространства является необходимой деталью выполнения программы изучения струнной структуры пространства – времени. Поск эффектов нарушения лоренц – инвариантности (LV) физических полей материи является элементом струнной программы. В этой статье изучается возможность вычисления по поляризационным параметрам электромагнитного излучения гамма – всплесков – самых мощных излучающих объектов в наблюдаемой Вселенной [1, 2].
Согласно [3], D – мерные поправки к лагранжиану электромагнитного поля представляют собой нелокальную часть конденсата, выпадающего в вакууме этого поля. В более ранних работах ряда американских групп теоретиков была показана перенормируемость этой теории (то есть, существование теории на каждом ее локальном уровне и существование фотонов). Для этого поправка на LV к лагранжиану D-мерной теории должна иметь в пределе D → ∞ нелокальный характер. Локальные модификации, развивавшиеся теоретиками вплоть до 2008 г., не прошли проверку этими критериями, и были отброшены. Очень важным теоретическим положенем является признание того, что формально-математический планковский масштаб Mg не «удерживает» в себе флуктуации пространства – времени. Эти флуктуации, видимо, могут проявляться при гораздо меньших значениях энергии физических полей и формально не быть связанными с Mg. В любом случае, этот вопрос должен решаться экспериментально. Вместо пятимерной поправки к лагранжиану поля [2] в [3] появляются гораздо болеее сложные структуры [3].
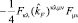(1)
где нелокальные слагаемые представляют собой ряды по производным:
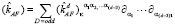(2)
СРТ – нечетное слагаемое,
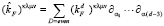(3)
СРТ – четное слагаемое.
Пусть параметр ξа выделяет направление поляризации световой волны, распространяющейся в трехмерном подпространстве (аналог осей 3-м сферы поляризационной Пуанкарэ [4]), но инденс «0» соответствует общему расширению Вселенной на расстоянии «z» от наблюдателя. Тогда дисперсионное соотношение соответствующее левой (правой) поляризации и сверхсветовому (досветовому) распространнию волны можно записать в виде:
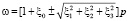. (4)
Здесь величины ξа могут быть разложены в ряд по сферическим функциям со спиновым весом Ньюмана – Пенроуза. Это, с одной стороны, позволяет выявить в изотропном пространве – времени все анизотропные эффекты (по аналогии с волновыми функциями атомной физики), а с другой учесть анизотропные эффекты типа двойного лучепреломления света в кристаллах и других средах. Спиновый вес сферических функций должен быть равен «2». Это соответствует возникающим в ходе двойного лучепреломления в среде спиновым состояниям. Действительно, правая и левая волна, по отдельности, несут спиновые состояния, равные «1» совсеми тремя возможными проекциями на выделенную в пространстве ось «z». Поэтому, их суперпозиция должна соответствовать спиновому состоянию «2». То есть, спиновый вес функции s = 2 формируется при сложении спинов лево (правополяризованных) фотонов s = 1 + 1 = 2. Это соответствует полному набору сферических гармоник в пространстве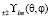 
, 
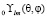. Знаки ± соответствуют левой (правой) поляризации излучения и, соответственно, (сверхсветовой, досветовой) фазовой скорости волны в пространстве. Необходимо подчеркнуть, что видимая картина распространения наблюдаемого поля в 4-м пространстве- времени является его видимой проекцией на 4-м многообразие из пространства-времени размерности D.
Кроме изменения законов электромагнитного поля, надо учесть изменение закона расширения Хаббла в D- мерной космологии. Связь в этой космологии между физическим временем t и красным смещением объекта z в общепринятой модели 
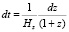(5)
где функция Hz имеет вид:
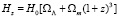
H0 – значение постоянной Хаббла в наше время,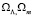 
параметры ускорения расширяющейся Вселенной.
Получим явное выражение для расстройки фазы ?φ – разницы фаз лево и право поляризованных волн в D – мерной теории гравитации.
Сначала оценим этот эффект в 3-м пространственной системе координат. Начнем с формул, не учитывающих явно космологическое расширение [5]:
1) разница во времени от принимаемых сигналов со сверхсветовыми и досветовыми скоростями есть:
2)
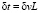, (6)
где L – расстояние до источника.
3) разница фаз между сверхсветовыми (левополяризованными) и досветовыми (правополяризованными) волнами есть:
4)
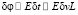(7)
Будем исходить из того, что эффект LV при размерности пространства
D = 4 отсутствует (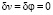
). Перепишем поправку к скорости света 
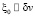и векторы поляризационных направлений с учетом космологического расширения через нормированный к нашей эпохе космологический фактор a/a0. Эти выражения примут вид:
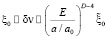(8)
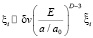(9)
где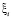 
– части поляризационных векторов, зависящие от угловых переменных.
Разность фаз можно рассчитать, исходя из общего выражения для волны электромагнитного поля с LV [3, с. 406]:
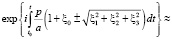
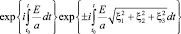(10)
Из (10) следет выражение для разности фаз левой и правой волн при существовании эффекта LV в D-мерном пространстве:
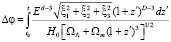(11)
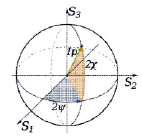
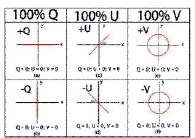
Рис. 1. Поляризационная сфера Гаусса в трёхмерном пространстве
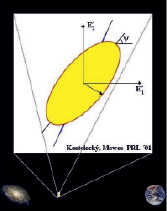
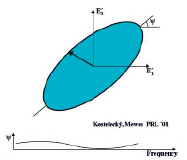
Рис. 2. Либрация поляризационного эллипса электромагнитной волны при ее распространении от удаленных источников в пространстве – времени к месту наблюдения
Теперь учтем, что квадратный корень
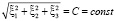(12)
ввиду того, что он является инвариантом относительно трехмерных вращений системы координат следуют осцилляторные решения для поляризационных осей сферы Гаусса, вписанной в 3-м пространство [3, с. 408]:
Оси поляризационной сферы U, Q, V осциллируют в мировом времени t вместе с фазой излучения ?φ
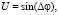
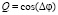(13)
Эти соотношения справедливы для поляризационных параметров всех послесвечений гамма-всплесков, наблюдения которых фиксируют линейную поляризацию излучения. Исключения из этого правила пока не обнаружены для всех измерений в области от оптического и до гамма-диапазона. Используем (2) c формулой для осцилляции поляризационных параметров произвольной константой С. Это позволяет вычислять точные значения поляризационных параметров U, Q, связывая их с размерностью пространства D:
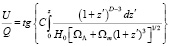. (14)
В общем случае, выразить D через поляризационные параметры не удается. Однако, существует приближение больших значений дополнительных размерностей пространства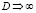 
. С помощью интегрирования по частям (14) получается формула:
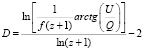, (15)
где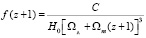 
.
То есть, размерность пространства и число его дополнительных измерений могут быть вычислены явно по показаниям поляризационных приборов, измеряющих параметры послесвечений космологических гамма-всплесков. Заметим, что рассчитанные осцилляции связаны с отклонением дисперсионных соотношений для фотонов от их классического аналога ω = k, связанного с появлением у фотона при ξ ≠ 0 малой эффективной массы покоя :
.
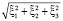Поэтому, рассматриваемый эффект осцилляций квантовых параметров фотонов является ближайшим «родственником» эффекта осцилляций состояний нейтринного поля [5].
Картина мира существенным образом зависит от наших космологических представлений. В свою очередь, эти представления складываются из знаний, полученных, как наблюдательным путем, так из активных ускорительных экспериментов. Разделить эти знания на независимые группы сегодня невозможно. Этот вывод иллюстрируется на примере, казалось бы, хорошо изученного электромагнитного поля.
Современная космология при большой неточности некоторых ее предсказаний и представлений имеет большое преимущество над ускорителями и другими наземными установками при изучении комплекса электромагнитное поле + гравитационное поле. Изучаемые в ней источники предельно высоких энергий дают возможность исследовать с помощью IPN источники огромных энергий, позволяющие судить о некоторых новых неизвестных ранее деталях строения электромагнитного и гравитационного полей. Постановка эксперимента по поиску осцилляций электромагнитного поля могла бы подтвердить новые теоретические идеи или опровергнуть их. Сегодня ясно лишь то, что предполагаемые будущие эксперименты по измерению значений поляризационных параметров могут как дать новую неожиданную информацию о размерности пространства, так и подтвердить теоретические предсказания или опровергнуть их.
Автор благодарен проф. МИФИ А.А. Петрухину, доц. МИФИ И.И. Яшину за ценные замечания.