При изучении общей топологии возникает необходимость рассматривать некоторые простые примеры топологических пространств, обладающие определенными свойствами. Наряду с такими топологическими пространствами, как стрелка, две стрелки, ковер Серпинского, можно рассмотреть топологическое пространство – лексикографически упорядоченный квадрат (см. рисунок).
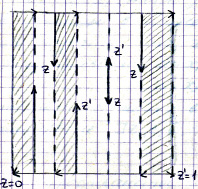
Лексикографически упорядоченный квадрат
1. Описание пространства.
Напомним определение нашего пространства.
Рассмотрим на плоскости OXY замкнутый квадрат со сторонами, параллельными осям координат и вершинами (0, 0), (0, 1), (1, 0), (1, 1) и упорядочим множество всех точек z = (x, y), 0 ≤ x ≤ 1,0 ≤ y ≤ 1 этого квадрата в лексикографическом порядке, то есть:
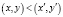, если 
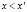или
если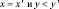 
.
Полученные в результате такого упорядочения порядковые интервалы и полуинтервалы [0, α[и] β, 1] образуют базу нашего пространства Q.
Эти интервалы имеют следующий вид: пусть даны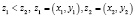 
, причем 
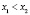, тогда для любой точки z, лежащей в полосе 
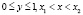, мы получим, что 
.
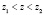Полуинтервалы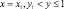 
и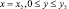 
также содержатся в порядковом интервале 
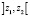, если 
.
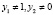2. Пространство является линейно упорядоченным и содержит наибольший и наименьший элемент.
Напомним, что
Определение 1. Множество X называется частично упорядоченным, если в нём установлено отношение порядка, удовлетворяющее условию транзитивности: если x < x' и x' < x'', то x < x''.
Определение 2. Если в данном частично упорядоченном множестве X отношение порядка установлено для любых двух различных элементов, то частично упрядоченное множество называется линейно упорядоченным
Теорема 1. Лексикографически упорядоченный квадрат Q является линейно упорядоченным множеством.
Определение 3. Если в данном упорядоченном множестве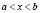 
, то говорят, что элемент x лежит между элементами a и b. Множество всех элементов x, лежащих между элементами a и b, называется интервалом ]a, b[ упорядоченного множества X.
Обозначим в пространстве Q точку (0, 0) символом 0, точку (1, 1) – символом 1, а любой элемент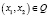 
– символом x, тогда открытыми множествами в Q являются 
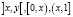, где 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 и всевозможные их пересечения.
Определение 4. Если элемент a частично упорядоченного множества X таков, что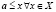 
, то a – первый (наименьший) элемент множества X.
Аналогичное определение даётся для наибольшего элемента.
В пространстве Q наименьшим элементом является 0, а наибольшим – 1.
То есть в пространстве Q имеются наименьший и наибольший элементы.
3. База топологии пространства Q.
Интервалы и полуинтервалы [0, ∞ [и] β, 1]образуют базу некоторой топологии на Q.
Имеется следующая теорема:
Теорема. Пусть X – множество, B – система его подмножеств. B является базой некоторой топологии на X, если выполняются условия:
a.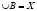 
(система B является покрытием X);
b.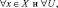 
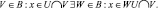
Условия a и b этой теоремы выполняются для наших интервалов и полуинтервалов. Следовательно, множество всех порядковых интервалов образуют базу некоторой топологии на Q.
4. Существование системы мощности c попарно не пересекающихся интервалов. Несепарабельность.
Рассмотрим интервалы вида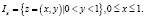 
Это вертикальные интервалы. Здесь x пробегает множество всех действительных чисел на [0, 1], то есть множество мощности c Для любых 
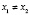имеем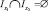 
. Интервалы являются открытыми множествами в Q.
То есть доказано существование системы не пересекающихся открытых множеств мощности c.
Докажем теперь несепарабельность Q. Напомним, что
Определение 5.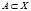 
– всюду плотное множество, если 
.
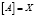Определение 6. X – сепарабельно, если в X существует счетное всюду плотное множество.
Рассмотрим произвольное всюду плотное множество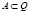 
. В любом из наших интервалов Ix имеется по крайней мере одна из точек множества A. Следовательно, мощность множества A не менее, чем континуум.
Следовательно, пространство Q несепарабельно.
5. Хаусдорфовость.
Определение 7. Хаусдорфовым топологическим пространством называется множество, в котором выделены некоторые подмножества, называемые открытыми множествами пространства, так что при этом выполняются следующие условия:
10. Всё пространство и пустое множество открыты.
20. Сумма любого числа и пересечение конечного числа открытых множеств есть открытое множество.
30. Ко всяким двум различным точкам x и y пространства имеются два непересекающихся множества Ox и Oy, содержащих соответственно эти точки.
Докажем хаусдорфовость нашего пространства Q.
Свойства 10 и 20 следуют из того, что Q – топологическое пространство.
Докажем свойство 30.
Пусть даны точки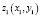 
, 
, 
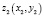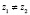. Тогда 
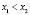или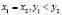 
.
А) Пусть x1 = x2, тогда существует x такой, что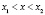 
, например, 
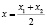, тогда 
, 
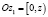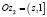, где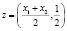 
.
Множества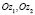 
открыты, 
, 
, 
.
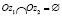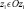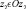B) Пусть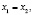 
тогда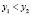 
, следовательно, 
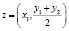, и мы снова получаем 
, 
.
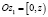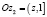Таким образом, пространство Q – хаусдорфово пространство.
Эти и другие свойства пространства Q можно изучать на семинарах по общей топологии в университетах.