Твердые растворы и интерметаллические фазы тройной системы Cu–Tl–Sn являются перспективными материалами в связи с их высокой электро- и теплопроводностью, коррозионной устойчивостью [4]. Фазовая диаграмма этой тройной системы, изученная в [5], находится в соответствии с характером фазовых равновесий граничных двойных систем Cu–Tl, Cu–Sn и Tl–Sn [7, 8]. В системе Cu–Tl имеет место расслоение жидких сплавов. При температуре монотектического равновесия 1241 К расслоение на жидкости охватывает область составов xCu = 0,17–0,855. Критическая температура растворимости равна 1533 К. Системы Cu–Sn и Tl–Sn характеризуются образованием ограниченных твердых растворов и интерметаллических фаз с областями гомогенности. Субсолидусная фазовой диаграмма тройной системы Cu–Tl–Sn, в основном, состоит из фаз на основе меди.
Целью данной работы является аналитический расчет и 3D моделирование поверхности кристаллизации меди и поверхности расслоения жидких сплавов в тройной системе Сu–Tl–Sn. Использована расчетная методика, апробированная в [1–3, 6] на системах Сu–Tl–Pb и Сu–Tl–Ge.
Результаты расчета и обсуждение
Моделирование поверхности кристаллизации меди
Уравнение аналитической модели поверхности кристаллизации компонента 1 компонента тройной системы 1–2–3 имеет вид
Т(123)(x, y) = y2?Т1(12) (х1) + (1 – y2)Т1(13) (х1) + + aх1(1 – х1)2y2(1–y2), (1)
где Т – температура, в К; y2 = x2/(1 – х1); (1–y2) = x3/(1 – х1); a – определяется по 3–5 измерениям ДТА для тройной системы. Т1(12) (х1) и Т1(13)(х1) – аналитические выражения ликвидуса двойных граничных систем. Уравнение (1) применительно к системе Cu–Sn–Tl имеет вид
Т(Cu–Sn–Tl) = ySnТ(Cu–Sn)(хCu) + + (1 – ySn)Т(Cu–Tl)(хCu) + + aхCu(1 – хCu)ySn(1–ySn), (2)
где y = xTl/(1 – хCu); (1–y) = xSn/(1 – хCu);
T(Cu–Tl) = 1358 – 1480(1 – xCu)y + + 4800(1 – xCu)2; (3)
Т(Cu–Sn) = 1358 – 600(1 – xCu) – – 8800(1 – xCu)2. (4)
Соотношения (3) и (4) с высокой точностью аппроксимируют кривые ликвидуса меди в двойных граничных системах Cu–Tl и Cu–Sn (таблица).
Подставляя аналитические выражения кривых ликвидуса меди в двойных граничных системах и значение параметра а в уравнение (2) получаем:
T = 1358 – 1480(1 – xCu)y + 4800(1 – xCu)2y – –600(1 – xCu)(1 – y) – 8800(1 – xCu)2(1 – y) + + 400xCu(1 – xCu)y(1 – y), (5)
где x = xCu; y = xTl/(1 – xСu).
Для упрощения функции T = f(x, y) в компьютерной программе уравнение (5) использовали в виде:
T = 1358 – 1480xy + 4800x2y – 600x(1 – y) – – 8800x2(1 – y) + 400x(1 – x)y(1 – y), (6)
где x = (1 – xCu) = 0–0,15; y = 0–1.
Поверхность кристаллизации меди в тройной системе Cu–Tl–Sn в интервале концентрации xCu = 0,845–1,0, вычисленная по уравнению (6), визуалирована на рис. 1.
Экспериментальные и расчетные данные для кривых кристаллизации меди в системах Cu–Tl и Cu–Sn в интервале концентрации xCu = 0,85–1,0
|
хCu(Cu–Tl) |
Т, К |
хCu (Cu–Sn) |
Т, К |
||
|
Эксп. [6] |
Расчет (3) |
Эксп. [6] |
Расчет (4) |
||
|
1,0 0,95 0,90 0,855 |
1358 1298 1256 1241 |
1358 1296 1258 1244 |
1,0 0,95 0,90 0,85 |
1358 1310 1207 1070 |
1358 1306 1210 1070 |
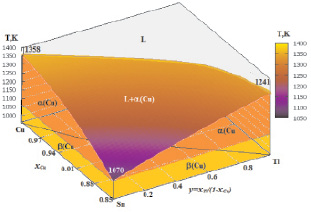
Рис. 1. 3D модель поверхности кристаллизации меди в системе Cu–Tl–Sn
Моделирование поверхности расслоения
Система Cu–Tl имеет фазовую диаграмму с монотектическим (1241 К) и эвтектическим (566 К) равновесиями. При температуре монотектики, область несмешиваемость расположена в интервале концентраций xCu = 0,17–0,845. Критическая температура растворимости (1533 К) уменьшается с добавлением олова [7]. Для расчета и моделирования поверхности расслоения жидких сплавов в тройной системе Cu–Tl–Sn использован следующий подход. Вначале определили аналитическое выражение кривой расслоения в системе Cu–Tl:
T, K = 1241 + 3330× ×(0,855 – y)(y – 0,17), (7)
где y = xCu/(xCu + xTl). Далее по экспериментальным данным измерений ДТА трех симметрично расположенных составов тройной системы определили функцию зависимости критической температуры растворимости от концентрации олова:
T, K = 1241 + 3330× ×(0,855 – y)(y – 0,17)(0,55 – xSn)0,5, (8)
которая позволила с высокой точностью вычислить и визуалировать поверхности расслоения в тройной системе Cu–Pb–Tl в интервале концентраций yCu = 0,17–0,855; xSn = 0–0,55 (рис. 2).
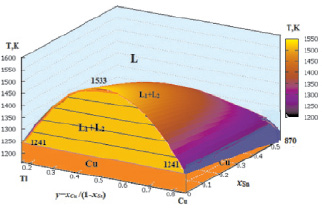
Рис. 2. 3D модель поверхности расслоения жидких сплавов в системе Cu–Tl–Sn
3D графики на рис. 1 и 2 отражают координаты моно- нонвариантных равновесий в системе Cu–Tl–Sn в температурной области 1000–1550 К [5]. В связи с высокой температуры затвердевания меди и его интерметаллидов, при охлаждении вначале выделяется медь или α(Cu), далее β(Cu) с малой областью гомогенности (рис. 1). Критическая температура растворимости в жидком состоянии с увеличением содержания олово уменьшается с 1533 К и достигает 870 К при xSn = 0,55 (рис. 2).
Заключение
Таким образом, на основании фазовых диаграмм граничных бинарных систем с использованием ограниченного числа данных ДТА получены в явном виде аналитические зависимости T = f(состав), позволившие рассчитать и 3D моделировать поверхности кристаллизации меди и расслоения жидких сплавов в системе Сu–Tl–Sn. Полученные 3D модели могут быть использованы для выбора условий получения сплавов системы Сu–Tl–Sn с заданными свойствами.

