В последнее время интерес вызывает визуализация некоторых абстрактных понятий, таких как последовательность чисел возведенных в степень, определенную целым числом. Для решения этой задачи потребовалось выделить две необходимых предпосылки:
1. Последовательность суммы натурального ряда чисел. Автор обозначил эту последовательность как I. Вот как она образуется:
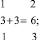
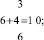
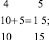
 (1)
(1)
2. Метод конечных разностей состоит в том, что от каждого последующего элемента последовательности отнимается предыдущий. В новой последовательности также от каждого последующего вычитается предыдущий элемент и так до того момента, пока эта разница станет постоянной. Все это изложено в результатах предыдущих исследований (S. Sirotkin, 2003, 2004). Итак, последовательность степенной функции третьей степени
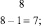
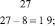
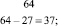
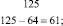
первая разность: 7, 19, 37, 61; вторая разность: 12, 18, 24; третья разность: 6, 6 (формула (2)).
Используя две эти предпосылки, мне удалось предложить две модели степенной функции третьей степени. Для моделирования использовался тетраэдр, половинки октаэдра и предложенный автором элемент Сиро. Одна модель трехгранная пирамида в ней любой член последовательности чисел возведенных в третью степень вычисляется по формуле:
n3 = (n – 1)3 + n2 + I(n–2) + 3?I(n–1). (3)
Вторая модель четырехгранная пирамида в ней любой член последовательности чисел возведенных в третью степень вычисляется по формуле:
n3 = (n – 1)3 + n2 + (n – 1)2 + 2I(n–1). (4)
Кроме элемента Сиро я предлагаю рассмотреть геометрические тела, такие как тетраэдр нулевого объема и тетраэдр двойного объема. Это предложение позволило расположить геометрические тела, имеющие одинаковую длину ребра в порядке кратного возрастания объемов.
Таким образом, представляется целесообразным распространить предложенную автором модификацию метода конечных разностей c использованием последовательности I на любой показатель степени и любое число, не только целое.

