Электропроводность металлов зависит от концентрации электронов проводимости n и от их подвижности l. Обе эти величины, являющиеся важными характеристиками, могут быть определены из опыта. Для измерения концентрации электронов можно пользоваться эффектом Холла. Эффект Холла наблюдается не только в металлах, но и в полупроводниках, причем по закону эффекта можно судить о принадлежности полупроводника к n- или р-типу.
Эффектом Холла называется явление перераспределения зарядов в металле или полупроводнике, через которые течет ток и которые помещены в магнитное поле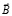 
, в результате чего возникает поперечная разность потенциалов между точками, расположенными на прямой, перпендикулярной как вектору 
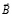поля, так и направлению тока 
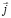(рис. 1). Причиной возникновения поперечной разности потенциалов является магнитная составляющая силы Лоренца, действующая на движущийся со скоростью 
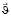заряд.
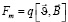. (1)
В результате действия силы отрицательные заряды отклоняются к верхней грани, на нижней появляется их недостаток – положительный заряд (рис. 1,а). Аналогично осуществляется перераспределение положительных зарядов (рис. 1,б). В предположении, что все носители тока имеют одинаковую постоянную скорость движения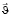 
и их концентрация n, сила тока через кристалл 
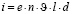, найдем:
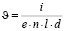. (2)
Из формулы (1) следует, что сторонняя сила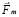 
создает поле 
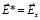, которое при 
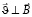приводит к появлению сторонней ЭДС – ЭДС Холла:
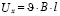. (3)
Из (2) и (3) получим:
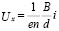. (4)
Величина
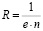(5)
является характеристикой вещества и называется постоянной Холла. Так как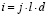 
, то напряженность поперечного электрического поля:
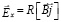. (6)
В реальном кристалле полупроводника носители тока испытывают столкновения по различным механизмам, рассеиваются на примесях и колебаниях решетки. Учет этих процессов для полупроводников с собственной (а) и примесной (б) проводимостью приводит к несколько отличным от (4) выражениям для R:
а)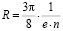 
б)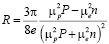 
(7)
где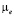 
, 
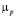– подвижность электронов и дырок, n и p их концентрации.
Установка для проведения эксперимента
В установке смонтированы механическая система перемещения датчика Холла вдоль оси соленоида с фиксацией его положения, блок-питания БП-1 соленоида, стрелочный прибор, регистрирующий ток соленоида, и электронная схема измерения, обеспечивающая регистрацию тока датчика Холла и ЭДС Холла (рис. 2).
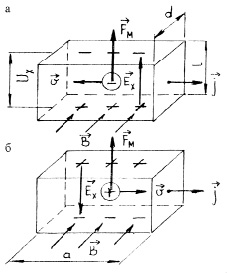
Рис. 1
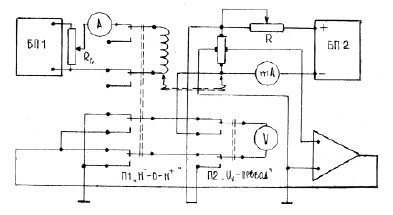
Рис. 2
При определении ЭДС Холла следует учитывать сопутствующие эффекты, которые, в отличие от эффекта Холла, являются четными по полю, т.е не зависит от направления поля. Это обстоятельство используется для их исключения, – Холловскую ЭДС измеряют при двух направлениях поля, изменяя его переключателем П1 «Н–О-Н+». при прямом направлении поля Н+ напряжение между Холловскими контактами U+=Uх+Uдоб, при обратном U-= –Uх+Uдоб, что после вычитания дает:
Uх=1/2(|U+|+|U-|), (8)
т.е. Uдоб, обусловленное четными эффектами, исключено.
Как следует из формулы (4), зависимость ЭДС Холла от величины индукции магнитного поля Ux=f(B) имеет линейный характер. Поэтому тангенс угла наклона прямой к оси абцисс (оси ОВ):
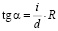. (9)
Откуда определяем постоянную Холла:
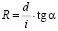. (10)
Используя формулу (7), а) можно найти концентрацию носителей:
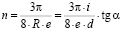. (11)
В положении переключателя П2 «провод» определяется удельное электрическое сопротивление кристалла датчика ρ по измеренному падению напряжения U и величине тока i:
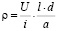. (12)
Так как
,
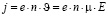где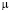 
– подвижность носителей тока, и 
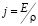, то
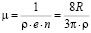. (13)
Эксперимент осуществляется в такой последовательности. Переключатель П2 перевести в положение «Uх». Потенциометром R задать ток через датчик и измерить ЭДС Холла при изменении магнитного поля соленоида в прямом и обратном направлении. Изменения знака поля осуществляется переключателем «Н-–О–Н+». Для этого датчик поместить на оси соленоида (обычно в центре), для которой известно зависимость индукции поля от тока через соленоид регулируемого потенциометром Rс. ЭДС Холла найти в результате двух измерений по формуле (8). Измерение повторяется несколько раз при других значениях тока через датчик Холла. Затем в положении переключателя П1–«О» и П2–«провод» снять зависимость тока через датчик Холла от разности потенциалов. Изменение напряжения осуществляется потенциометром R. Далее снять распределение поля по оси соленоида в положении П2–«Uх».
По результатам экспериментальных материалов:
Построить зависимость Uх=ƒ(В) (градуированную кривую датчика Холла), через полученные точки провести прямую, найти тангенс угла её наклона к оси абсцисс по формуле (10) определить постоянную Холла, а по зависимости (11)-концентрацию носителей.
Проверить выполняемость закона Ома для датчика Холла, для чего построить зависимость U=ƒ(i) провести через полученные точки прямую линию и найти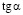 
угла её наклона к оси i. По формуле, следующей из (12),
.
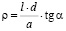Определить удельное сопротивление кристалла, а по зависимости (13) – подвижность носителей заряда. Студенты выполняют и другие лабораторные работы: эффект Доплера, определение ширины запрещенной зоны полупроводника, проверяются законы волновой оптики с применением гелий – неонового лазера и т.д.
Студенты убеждаются, что эффект Холла является наиболее эффективным методом изучения энергетического спектра носителей тока в металлах и полупроводниках.