Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Рассмотрим моделирование поверхности на плоскости, используя различные аппараты проецирования и основные требования моделирования для получения в качестве моделей взаимно однозначных соответствий [1].

Поверхность Ф2 второго порядка в методе двух изображений, т.е. когда аппаратом проецирования являются две связки прямых, на плоскости моделируется (2÷2) – значным квадратичным соответствием 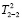, устанавливаемым между горизонтальными 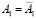и фронтальными 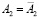проекциями точки 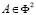. Здесь дву–двузначное соответствие означает, что 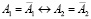, а квадратичное – прямой a1 горизонтальной проекции ставится в соответствие коника 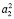фронтальной плоскости проекций.

Поверхность 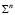порядка n в методе двух изображений моделируется (n÷n) – значным соответствием n-го порядка, устанавливаемом между полями проекций. Отсутствие законченной теории многозначных соответствий не позволяет по такой модели поверхности исследовать ее свойства. Поэтому возникает актуальная проблема начертательной геометрии и алгебраической геометрии, связанная с получением в качестве модели поверхности взаимно однозначного соответствия [2].

Рассмотрим условия моделирования поверхностей 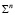порядка n в методе двух изображений (1÷1) – значными соответствиями.

Чтобы поверхность 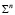порядка 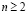моделировалась на плоскости (1÷1) – значным соответствием, необходимо подбирать соответствующий аппарат проецирования. Например, квадрика Ф2 моделируется (1÷1) – значным соответствием, если центры вспомогательного проецирования инцидентны квадрики (стереографическое проецирование). При этом соответствия, получаемые на плоскости изображения, могут быть инволюционными или не инволюционными, но обязательно центральными.

Поверхности высших порядков 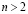моделируются (1÷1)-значным соответствием, если они имеют не менее двух (n–1)-кратных точек, в которые помещаются центры стереографического проецирования. Модели таких поверхностей, получаемые в методе двух изображений, будут центральными и нелинейными. Поверхности 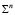для 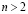моделируются (1÷1) – значными соответствиями, если в качестве аппаратов проецирования используются связки прямых, конгруэнции прямых Кг(1,k) первого порядка и k класса или специальные комплексы прямых Km(n).

Все возможные варианты сочетаний проецирований составляющих аппараты отбражения в методе двух изображений сведены в табл. 1 [3].

Поверхность Ф2 второго порядка в методе двух изображений, т.е. когда аппаратом проецирования являются две связки прямых, на плоскости моделируется (2÷2) – значным квадратичным соответствием 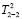, устанавливаемым между горизонтальными 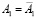и фронтальными 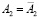проекциями точки 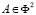(рис. 1). Здесь дву–двузначное соответствие означает, что 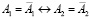, а квадратичное – прямой a1 горизонтальной проекции ставится в соответствие коника 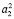фронтальной плоскости проекций. A1~ A2, , .

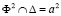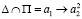Таблица 1

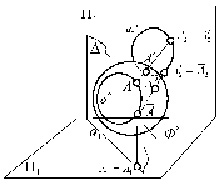
Рис. 1

Далее рассмотрим моделирование сферы Ф2 при помощи стереографического проецирования из центров S1 и S2, причем 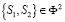, на плоскость проекций П. При этом каждая точка 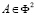, за небольшим исключением, будет моделироваться парой соответственных точек A1~ A2 инцидентных прямой 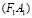(рис. 2), где 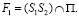Исключение составляют точки S1 и S2. При перемещении точки A по сфере Ф2, когда точка 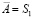из центра S1 будет проецироваться на плоскость P множеством прямых, образующих касательную плоскость 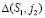к сфере Ф2 в точке S1, то есть точка 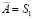проецируется на плоскость P из точки S1 прямой 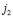. Из центра S2 точка 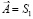проецируется в точку 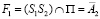, значит моделью точки 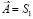на плоскости P будет прямая 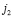и точка F1, аналогично – моделью точки 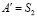из центра S2 на плоскость P будет прямая 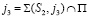, а из центра S1 точка 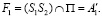Нарушение взаимно однозначного соответствия при стереографическом проецировании сферы Ф2 на плоскости P получается при проецировании точек 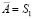и и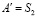з центров проецирования S1 и S2 соответственно при этом прямые 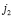и , будут исключенными (фундаментальными) прямыми этого отображения.

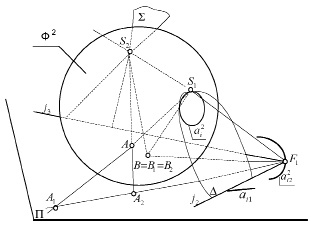
Рис. 2

Прямая (S1, S2) является двойной прямой пространства, так как она проецирует две точки S1 и S2, а точка F1, двойной точкой плоскости P. В рассматриваемом случае, сфера Ф2 касается плоскости П в точке B, которая из центров проецирования S1 и S2 проецируется на плоскость P в точки B1 и B2. Они совпадают с точкой B, то есть 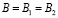, полученная точка 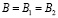то же двойная точка плоскости P. Если бы сфера Ф2 пересекала плоскость P, то на плоскости P была бы целая окружность двойных точек, такая окружность называется инвариантной кривой линией преобразования, а точка 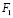инвариантная точка преобразования или модели сферы Ф2 на плоскость P.

Все окружности связки (S1) окружностей сферы Ф2 проецируются из центра S1 на плоскость П в прямые, так как связка (S1) плоскостей, несущая связку (S1) окружностей сферы Ф2, пересекает плоскость П по прямым 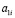. Значит двупараметрическое множество окружностей связки (S1) окружностей сферы проецируется на плоскость П в двупараметрическое множество прямых. Связка (S1) окружностей сферы Ф2 из центра S2 проецируется на плоскость P связкой (F1) окружностей 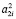, так как все конические поверхности 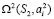, проецирующие окружности 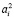инциденты прямолинейной образующей (S1S2), где 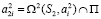. Любая окружность 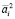сферы Ф2 не инцидентная центрам S1 и S1 будет моделироваться на плоскость P парой окружносте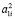й и 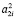, получаемых как результат пересечения конических поверхносте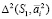й и 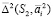с плоскостью P. Пучок окружностей 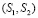сферы Ф2 будет моделироваться на плоскости P прямыми пучка (F1) прямых, получаемых в пересечении пучка (S1, S2) плоскостей, несущих пучок (S1, S2) окружностей сферы Ф2, с плоскостью P.

При моделировании поверхности на плоскости или на другой поверхности необходимо, чтобы существовала взаимосвязь оригинала (поверхности Ф2), аппарата проецирования (двух связок (S1) и (S2) прямых) и модели. В рассмотренном примере эта связь организована в расслоении поверхности Ф2 в пучке (S1, S2) плоскостей. Соответствия порождаемые на лучах пучка (F1) прямых, в общем случае, будут параболического, гиперболического или эллиптического типов. В нашем примере только на луче 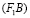будет параболическое соответствие между проекциями точек A1~ A2, на остальных лучах пучка (F1) прямых будет эллиптические соответствия. Моделью сферы Ф2 на плоскость P будет инволюция, однозначно определяемая центром 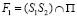и инвариантной окружностью 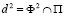, если точка 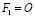, где O – центр инвариантной окружности в остальных случаях моделью сферы Ф2 на плоскости проекций П будет взаимно однозначное квадратичное соответствие T2, так как, если на плоскости П взять точку A1, отнесенной к первичной проекции точки 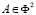и пусть точка A перемещается по прямой 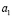, которая из центра S1 будет проецироваться плоскостью 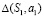, пересекающей сферу Ф2 по окружности 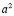, которая из центра 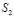проецируется конической поверхностью 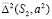, пересекающей плоскость проекции P по окружности 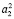соответствующей прямой 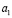в соответствии T2. Значит, точка A2~A1 будет перемещаться по окружности 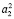. Соответствие T2 будет инволюционным, если плоскость проекций P будет биссекторной плоскостью двугранного угла, образованного касательными плоскостям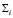и и 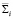к сфере в точках 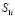и 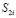, которое обозначается .

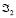На рассмотренных выше примерах четко прослеживается тесная связь типа модели оригинала от взаимного положения аппарата проецирования относительно оригинала и плоскости проекции, а так же расположения плоскости проекций относительно оригинала. Наиболее простые модели оригиналов являются инволюционными соответствиями.

Далее, в качестве примера, рассмотрим моделирование эллипсоида вращения 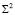при помощи стереографического проецирования из центров S1 и S2, инцидентных поверхности эллипсоида вращения 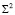, на плоскости проекций P совмещенной с его плоскостью симметрии перпендикулярно прямой (S1S2). Рассмотрим аналитическое моделирование эллипсоида вращения, заданного каноническим уравнением:

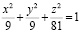, (1)

центр, которого помещен в начало координат. Поэтому уравнение инвариантной окружности 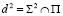, получается подстановкой в (1) значения z=0:

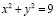. (2)

Центры проецирования (вершины эллипсоида) имеют координаты 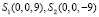. В этом случае центром преобразования является точка

.

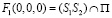Покажем, что моделью эллипсоида вращения 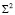является инволюционное квадратичное соответствие – инверсия. Возьмем на эллипсоиде 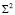некоторую точку A(2,1,6) и запишем уравнение прямой (S1 A):

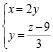. (3)

Найдем точку A(–6,–3) пересечение прямой (S1 A) с плоскостью P, подставив в (3) значение 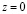. Аналогичными выкладками найдем координаты точки 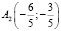проекции точки A из центра S2. Точки A1 и A2 соответственны в полученном преобразовании и коллинейны с центром преобразования F1. Прямая 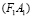пересекает инвариантную окружность 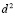в двойных точках 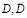, которые с точками A1,A2 составляют гармоническую четверку точек, то есть 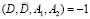, что в координатной форме запишется так:

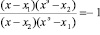, (4)

где 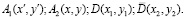Координаты точек D и 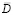находим, решая систему уравнений:

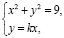(5)

где 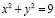– уравнение инвариантной окружности 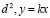– уравнение прямой 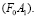Имеет координаты точек:

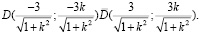
Подставляя координаты точек 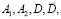в (5) и выполняя упрощения, получим формулы прямого преобразования:

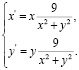(6)

Таким образом, мы имеем на плоскости P квадратичное, инволюционное преобразование – инверсию.

Если точка A1(–6,–3) будет перемещаться по прямой a1:

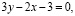(7)

то, решая совместно (7) и (6), получим уравнение окружности на которой лежит точка 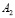(–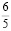; – 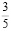), соответственная точке A1. Этот результат говорит о том, что любая коника эллипсоида вращения 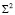, инцидентная центру S1 (или S2), проецируется на плоскость P в окружность.

Как было отмечено раньше, чертеж модулируемой поверхности должен быть обратимым. Это значит, что по одной проекции, например, A1 точки A поверхности можно построить вторую проекцию A2. На полученной модели эллипсоида вращения 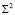это возможно, так как имея проекцию A1, строим ей инверсную точку A2 относительно инвариантной окружности d2.

Вывод

Таким образом, имея модель поверхности 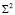, можно решать любые позиционные задачи. Например, пусть требуется построить точки пересечения поверхности эллипсоида вращения 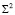с прямой 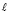. На плоскости P эллипсоид 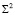моделируется (задается) инверсией 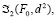а прямая 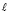задается свободными проекциями 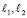(рис. 3).

Рис. 3

Отнесем прямую 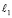к полю 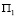и построим ее образ 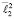в инверсии ℑ2 . Точки пересечения окружности 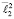с прямой 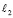суть вторичные проекции L2,M2 точек пересечения прямой 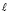с эллипсоидом вращения 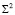. Затем строим первичные проекции L1,M1 точек пересечения, как образов точек L2,M2 в инверсии ℑ2. Здесь инверсия 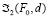является моделью для множества эллипсоидов вращения, имеющих уравнения вида:

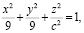(15)

где c – любое положительное число.