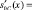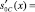Большинство современных систем на кристалле (СнК), которые нашли широкое применение в современных инфокоммуникационных системах, для защиты передаваемой информации от несанкционированного доступа используют криптографические алгоритмы шифрования. Наличие в современных системах на кристалле блока криптообработки позволяет эффективно их использовать при проектировании портативных радиостанций, систем управления и передачи высокоскоростной информации для больших и малых беспилотных летательных аппаратов, наземных роботов, интеллектуальных сенсорных сетей, а также широкополосных систем гражданского назначения (4–5) G стандарта [5, 8]. Особое место среди алгоритмов шифрования стандарт AES. При этом использование данного алгоритма шифрования в различных сферах привело к повышенному числу атак на AES [4, 7, 10].
Среди криптоатак особое место занимают атаки, которые используют информацию, полученную по побочным каналам. Как правило, такие криптоатаки строятся на основе сбоев, принудительно вызываемых в работе шифратора. Снизить эффективность реализации атак на основе сбоев можно за счет использования корректирующих кодов полиномиальной системы классов вычетов (ПСКВ). Поэтому разработка алгоритма поиска и коррекции ошибок, возникающих в процессе шифрования AES, является актуальной задачей.
Основная часть
Эффективность работы современных высокопроизводительных СнК во многом определяется наличием на кристалле не только процессорных ядер общего назначения, но и специализированных вычислительных модулей. При этом наряду с вычислительными ускорителями в состав СнК стали чаще вводиться блоки криптографической защиты, что наглядно проявляется в в чипах линейки Marvell Armada, Sitara Am38x и TI OMAP [5, 8].
Для обеспечения высокого уровня достоверности и конфиденциальности передаваемой и обрабатываемой информации в СнК широко применяется алгоритм шифрования AES (до проведения конкурсного отбора Rijndael). Выбор данного алгоритма криптозащиты, согласно [7], определяется хорошим сочетание криптографической стойкости, производительности, а также относительно низкими требованиями к аппаратурным затратам и платформам.
Однако, несмотря на отмеченные выше достоинства, блочный алгоритм шифрования AES, постоянно подвергается проверке на криптостойкость. Проводимые атаки на стандарт шифрования AES можно разделить на виды – атаки методом бумеранга; атаки на основе модификации методов криптоанализа на связанных ключах; алгебраические атаки; атаки, использующие информацию, полученную по побочным каналам (side-channel-атакам) [4].
В статье будут рассмотрены атаки последнего вида, которые относятся к активным атакам. В их основу положены различные воздействия на шифрующее устройство, которые осуществляются с целью внести искажения в информацию на различных этапах шифрования. В качестве основных мер воздействия на шифратор можно выделить – увеличение напряжения питания криптосистемы, изменение частоты шифрующего устройства, при котором частота значительно превышает максимально допустимую, помещение конструкции в электромагнитное поле, повышение температуры некоторой части шифратора. Для защиты от атаки используют добавление в шифрующий механизм датчиков воздействий, блокирующих шифратор при ненормальных параметрах системы, вычисление контрольной суммы, экранирование шифратора [4].
Однако представленные выше алгоритмы не учитывают особенности алгоритма шифрования, что приводит к значительным затратным решениям. Повысить эффективность противодействия этим криптоатакам можно за счет корректирующих кодов ПСКВ.
Алгоритм AES относится к симметричным системам шифрования, в основу которого положен математический аппарат поля Галуа GF(28) с порождающий полиномом m(x) = x8 + x4 + x3 + x + 1. Выбор такого порождающего полинома позволяет выполнять криптографические операции над байтами, которые рассматриваются как элементы конечного поля GF(28). Использование ПСКВ позволяет перейти к аналогичным операциям, которые эффективно можно реализовать в полях меньшей размерности GF(24). В этом случае неприводимые полиномы m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1, которые являются порождающими многочленами, можно использовать в качестве рабочих оснований ПСКВ. Согласно [1, 2, 9] использование двух оснований m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1 позволяет осуществлять в ПСКВ операции модульные проводить параллельно, помодульно и независимо
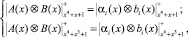 (1)
(1)
где ⊗ – операции сложения, вычитания и умножения в GF(p); A(x) = (α1(x), α2(x), ..., αk(x)) и B(x) = (b1(x), b2(x), ..., bn(x)); α1(x) ≡ A(x)mod m1(x); b1(x) ≡ B(x)mod m1(x); l = 1, …, k.
Наряду с высокой скоростью выполнения вычислений коды ПСКВ способны обнаруживать и исправлять ошибки, которые возникают из-за отказа и сбоев оборудования [6]. Для обеспечения коррекции ошибок при работе алгоритма шифрования AES предлагается использовать многочлен m3(x) = x4 + x3 + x2 + x + 1. В работе [1] показан алгоритм вычисления синдрома ошибки для кода ПСКВ, использующего одно контрольное основание, который позволяет обнаруживать факт наличия ошибок, вызванных сбоями в работе устройства. Для обнаружения и исправления однократной ошибки в коде ПСКВ A(z) = (α1(x), α2(x), ..., αk(x)) вводят избыточное основание deg mk + 1(x) ≥ deg mk(x). Для коррекции однократной ошибки в коде ПСКВ вычисляют два контрольных остатка
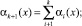
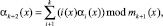 (2)
(2)
где i(x) – полиномиальная форма i-го номера; Σ – суммирование по модулю два.
Чтобы обнаружить однократную ошибку в комбинации ПСКВ вычисляются значения
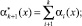
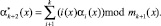 (3)
(3)
Значения 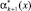 и
и 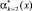 , используются для вычисления синдрома ошибки
, используются для вычисления синдрома ошибки
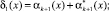
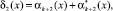 (4)
(4)
Если синдром ошибки равен нулю, то есть δ1(x) = 0 и δ2(x) = 0, то комбинация ПСКВ не содержит ошибки. В противном случае – комбинация ПСКВ содержит ошибку. При этом по величине синдрома ошибки δ1(x) и δ2(x) можно однозначно определить местоположение и глубину ошибки в модулярном коде ПСКВ.
Анализ, представленного в работе [1], алгоритма поиска и коррекции ошибок в модулярном коде ПСКВ показывает, что данный алгоритм можно эффективно применить для противодействия атакам на основе, проводимых на алгоритм шифрования AES. Известно, что каждый раунд алгоритма AES состоит из четырех преобразований – замены байтов SubBytes, побайтового сдвига строк Shift Rows, перемешивания столбцов MixColums, сложение с раундовым ключом AddRoundKey.
Применение избыточного кода ПСКВ потребует внесения определенных аппаратных изменений в структуру шифратора AES. В работе [3], приведен алгоритм применения корректирующего кода ПСКВ при реализации базовой процедуры замены блоков в алгоритме шифрования AES. Суть его состоит в том, что для получения кода ПСКВ байт открытого текста S поступает на вход преобразователя из позиционного кода в код ПСКВ, с выхода которого снимаются значения двух остатков s1(x) ≡ S(x)mod m1(x), s2(x) ≡ S(x)mod m2(x).
Затем два четырехразрядных блока данных, определяемые текущим байтом S(x), поступают на входы преобразователя SubBytes, который представляется в виде двух таблиц размером 256×4 бит. После выполнения операции подстановки проводится проверка на наличие ошибок в коде ПСКВ. Для этого согласно (3) вычисляются значения проверочных остатков по модулю m3(x) = x4 + x3 + x2 + x + 1. Затем происходит вычисление синдрома ошибки согласно (4). При необходимости, ошибка будет исправлена.
После этого результат операции подстановки, представленный по двум информационным основаниям m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1, подвергается следующим раундовым преобразованиям – побайтовом сдвиге строк Shift Rows, перемешивании столбцов MixColums; сложение с раундовым ключом AddRoundKey. Рассмотрим применение корректирующего кода ПСКВ при проведении операции перемешивания столбцов MixColums. В этом преобразовании столбцы состояния рассматриваются как многочлены над расширением поля Галуа GF(28) и умножаются по модулю двучлена x4 + 1 на многочлен
g(x) = {03}x3 + {01}x2 + {01}x + {02}.
Данную операцию в матричном виде можно представить как
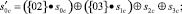
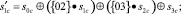 (5)
(5)
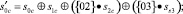
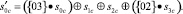
где с – номер столбца массива State; {02} – соответствует умножению на х; {03} – соответствует умножению на х + 1.
При этом умножение байтов массива State на {02} и на {03} выполняются по модулю m(x) = x8 + x4 + x3 + x + 1. Пусть на вход преобразователя MixColums поступил 32-битовый столбец s0C = CA; s1C = D1; s2C = E2; s3C = 4F. В избыточном коде ПСКВ эти байты, представленные в 16-ричной системе счисления, имеют вид CA = (D, 2, F, 9), D1 = (5, 0, 5, 5), E2 = (3, 1, 2, 1), 4F = (3, 0, 3, 3). Рассмотрим получение нового значения байта
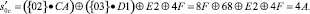
Таблица 1
Остатки результата умножения x?sj(x)mod x4 + x + 1
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
F |
9 |
6 |
8 |
7 |
1 |
E |
E |
1 |
7 |
8 |
6 |
9 |
F |
0 |
|
1 |
D |
2 |
4 |
B |
5 |
A |
C |
3 |
3 |
C |
A |
5 |
B |
4 |
2 |
D |
|
2 |
D |
2 |
4 |
B |
5 |
A |
C |
3 |
3 |
C |
A |
5 |
B |
4 |
2 |
D |
Информационные остатки первого байта CA = (D, 2) поступают на входы табл. 1 и 2. Представленная часть табл. 1 содержит остатки результата умножения, приведенной по модулям m1(x) = x4 + x + 1. На пересечении второй строки и столбца D располагается остаток 4 = 0100 = x2.
Табл. 2 содержит результат умножения x?sj(x) по модулю m2(x) = x4 + x3 + 1. На пересечении второй строки и столбца D располагается остаток 8 = 0100 = x3.
Кроме того, информационные остатки первого байта CA = (D, 2) поступают на входы табл. 3 и 4. Табл. 3 содержит данные о сумме остатков информационных оснований ПСКВ. На пересечении 2 строки и столбца D находится остаток C = 1100 = x3 + x2.
В табл. 4 представлены данные о втором контрольном остатке. На пересечении 2 строки и столбца D находится остаток B = 1011 + x3 + x + 1.
Таким образом, после выполнения операции умножения имеем
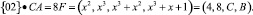
Таблица 2
Остатки результата умножения x?sj(x)mod x4 + x3 + 1
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
C |
C |
0 |
0 |
C |
C |
0 |
C |
0 |
0 |
C |
C |
0 |
0 |
C |
|
1 |
E |
2 |
2 |
E |
E |
2 |
2 |
E |
2 |
E |
E |
2 |
2 |
E |
E |
2 |
|
2 |
8 |
4 |
4 |
8 |
8 |
4 |
4 |
8 |
4 |
8 |
8 |
4 |
4 |
8 |
8 |
4 |
Таблица 3
Первый контрольный остаток α3(x)
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
3 |
5 |
6 |
8 |
B |
D |
E |
2 |
1 |
7 |
4 |
A |
9 |
F |
C |
|
1 |
3 |
0 |
6 |
5 |
B |
8 |
E |
D |
1 |
2 |
4 |
7 |
9 |
A |
C |
F |
|
2 |
5 |
6 |
0 |
3 |
D |
E |
8 |
B |
7 |
4 |
2 |
1 |
F |
C |
A |
9 |
Таблица 4
Второй контрольный остаток α4(x)
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
8 |
E |
6 |
8 |
0 |
6 |
E |
9 |
1 |
7 |
F |
1 |
9 |
F |
7 |
|
1 |
E |
6 |
0 |
8 |
6 |
E |
8 |
0 |
7 |
F |
9 |
1 |
F |
7 |
1 |
9 |
|
2 |
2 |
A |
C |
4 |
A |
2 |
4 |
C |
B |
3 |
5 |
D |
3 |
B |
D |
5 |
Рассмотрим умножение второго состояния D1 = (5, 0, 5, 5) на коэффициент на {03}. Данную операцию можно представить в виде
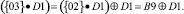
Чтобы получить первое слагаемое воспользуемся табл. 1–4. На пересечении 0 строки и 5 столбца находится остаток:
– в табл. 1 (первый информационный остаток) – 716 = 0111 = х2 + х + 1;
– в табл. 2 (второй информационный остаток) – С16 = 1100 = х3 + х2;
– в табл. 3 (первый контрольный остаток) – В16 = 1011 = х3 + х + 1;
– в табл. 4 (второй контрольный остаток) – 016 = 0000.
Полученный результат складываем по модулю два с D1 = (5, 0, 5, 5). Тогда
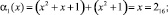
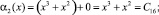
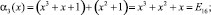
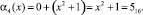
Тогда имеем результат умножения на {03}
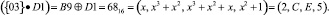
В табл. 5 показано суммирование полученных результатов.
Таблица 5
Результат вычисления нового состояния 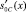
|
α1(x) |
α2(x) |
α3(x) |
α4(x) |
|
|
8F = |
х2 |
х3 |
х3 + х2 |
х3 + х + 1 |
|
68 = |
х |
х3 + х2 |
х3 + х2 + x |
х2 + 1 |
|
E2 = |
х + 1 |
1 |
х |
1 |
|
4F = |
х + 1 |
0 |
х + 1 |
х + 1 |
|
|
х2 + x |
х2 + 1 |
х + 1 |
х3 + х2 |
В результате получили новое состояние
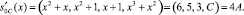
Проведем проверку контрольных оснований согласно (3). Получаем
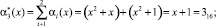
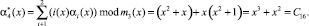
Воспользуемся равенством (4), чтобы вычислить синдром ошибки
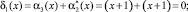
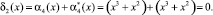
Значит, ошибка отсутствует – сбоя в процессе работы шифратора AES не было.
Пусть в результате сбоя произошло искажение первого слагаемого и ошибка произошла по первому остатку, а глубина ошибки равна Δα1(x) = 1. Тогда с выхода табл. 1 будет снят остаток 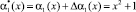 . Тогда имеем комбинацию
. Тогда имеем комбинацию
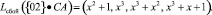
В табл. 6 показано суммирование полученных результатов.
Таблица 6
Результат вычисления нового состояния 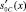
|
α1(x) |
α2(x) |
α3(x) |
α4(x) |
|
|
8F = |
х2 + 1 |
х3 |
х3 + х2 |
х3 + х + 1 |
|
68 = |
х |
х3 + х2 |
х3 + х2 + x |
х2 + 1 |
|
E2 = |
х + 1 |
1 |
х |
1 |
|
4F = |
х + 1 |
0 |
х + 1 |
х + 1 |
|
|
х2 + x + 1 |
х2 + 1 |
х + 1 |
х3 + х2 |
В результате получили новое состояние
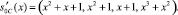
Проведем проверку контрольных оснований согласно (3). Получаем
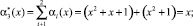
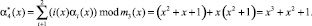
Воспользуемся равенством (4), чтобы вычислить синдром ошибки
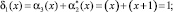
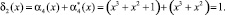
В результате получили, что синдром ошибки отличен от нуля. Это свидетельствует о том, что код содержит ошибку, вызванную сбоем в работе шифратора. По значению синдрома ошибки δ1(x) =1 и δ2(x) =1 из памяти берется вектор ошибки, который равен 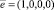 . Данный вектор ошибки складываем с ошибочно комбинацией
. Данный вектор ошибки складываем с ошибочно комбинацией
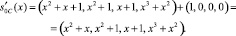
Таким образом, ошибка, вызванная из-за атаки на основе сбоев, была устранена.
Выводы
Обобщая полученные результаты, можно сделать вывод о том, что разработанный алгоритм поиска и коррекции ошибок с помощью избыточного кода ПСКВ позволяет не только обнаруживать, но и исправлять ошибки. То есть данный алгоритм способен устранять последствия атаки на основе сбоев на алгоритм шифрования AES.