Поиск точных решений стационарного уравнения Шрёдингера является пограничной областью между физикой и математикой. Как правило, физикам известен очень ограниченный набор таких решений. Однако, такие решения могут быть найдены для многих систем электромагнитного и сильного взаимодействий, таких как молекулы, атомы и кварконии. Для поиска этих решений выделим несколько классов потенциалов, обладающих конформной симметрией, и найдём решения для этих классов. Затем, приспособим найденные решения к конкретным 2-х и 3-х параметрическим потенциалам квантовых систем, хорошо известных в физике электромагнитного и сильного взаимодействий.
Как известно [1], уравнение Шрёдингера в координатном представлении
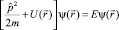 (1)
(1)
после введения цепочки лестничных пары лестничных операторов
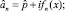
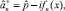
сводится к нелинейному операторному уравнению Риккати для операторной функции fn = fn(x) в координатном представлении:
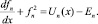 (2)
(2)
Цепочка операторов {En} образует спектр оператора гамильтона 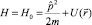 .
.
Для простоты, не будем писать шляп над операторами.
Цепочка операторов {Hn} факторизуется
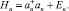
Для нахождения спектра En рассмотрим одномерное движение fn = fn(q) и построим I класс точно решаемых задач для потенциалов
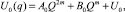 (3)
(3)
где m – произвольное действительное число; Q = Q(x) – некоторая функциональная форма, которую необходимо задать.
Будем искать точное решение уравнения (2) в виде
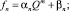
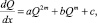 (4)
(4)
где αn, βn – цепочки функций, подлежащих определению; a, b, c – известные константы.
Поставленная задача требует нахождения цепочек αn, βn, En, в виде функций констант A0, B0, U0, a, b, c.
Собирая коэффициенты при одинаковых степенях Q в уравнениях (3)–(4), получим следующие уравнения для неизвестных α0, β0, E0:
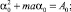
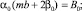 (5)
(5)
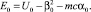
Операторы цепочки находятся по рекуррентной формуле
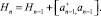 (6)
(6)
Построим первый оператор цепочки (2)
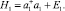
Собирая коэффициенты при одинаковых степенях Q, построим систему уравнений для коэффициентов, подлежащих определению.
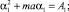
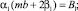 (7)
(7)
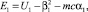
где
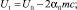
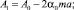
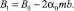
Для уравнений цепочки с индексом n получим
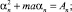
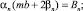 (8)
(8)
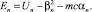
Из (8) следуют тогда решения
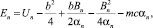 (9)
(9)
где
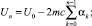
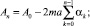 (10)
(10)
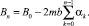
Решение уравнения (9) даёт
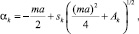 (11)
(11)
где знак sk = ±1, 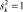 устанавливается с учётом условий максимальности уровней энергии при факторизации.
устанавливается с учётом условий максимальности уровней энергии при факторизации.
Из (11) следует, что при k = 0
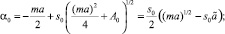 (12)
(12)
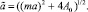
Тогда
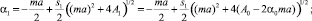
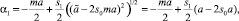 (13)
(13)
то есть, 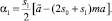
Продолжая эту процедуру, получим
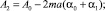
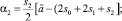
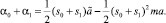 (14)
(14)
Продолжая эту процедуру по индукции, получаем
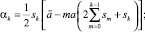 (15)
(15)
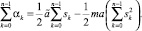
Упорядоченный дискретный спектр En будет существовать только при sk = s.
Тогда из выражений (15) следует
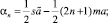
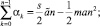 (16)
(16)
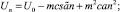
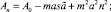 (17)
(17)
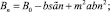
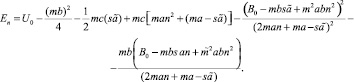 (18)
(18)
I-1. Линейный гармонический осциллятор.
Пусть m = 1, U0 = B0 = 0, a = 0, b = 0, c = 1.
Потенциал линейного гармонического осциллятора имеет вид:
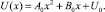 (19)
(19)
Отсюда следует
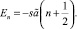 (20)
(20)
Из (19) видно что s = –1 и, следовательно,
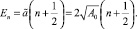 (21)
(21)
Подставляя в (20) 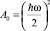 получаем стандартный спектр.
получаем стандартный спектр.
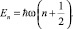 (22)
(22)
I-2. Нелинейный осциллятор.
Рассмотрим потенциал
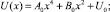 (23)
(23)
m = 2, U0 = B0 ≠ 0;
a ≠ 0; b = 0; c = 1.
Полагая 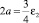 ,
, 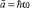 , получаем из (18), (19) спектр нелинейного осциллятора, совпадающий с [2] с точностью до первого порядка теории возмущений (второй член в (22), a << 1).
, получаем из (18), (19) спектр нелинейного осциллятора, совпадающий с [2] с точностью до первого порядка теории возмущений (второй член в (22), a << 1).
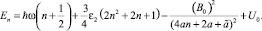 (24)
(24)
C более высокими порядками ТВ рассматриваемый спектр может совпасть при отличных от нуля коэффициентах A0, B0, U0, b = 0, a << 1.
I-3. Потенциал Леннарда – Джонса.
Молекулярный потенциал Леннарда – Джонса имеет вид:
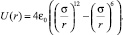 (25)
(25)
То есть, m = –6; A0 = 4ε0σ12; B0 = 4ε0σ6; U0 = 0; a, b, c ≠ 0.
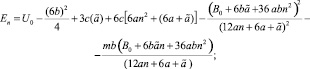 (26)
(26)