Моделирование радиолокационных сигналов, переизлученных земными средами в настоящее время остается актуальной. Существующие в настоящее время электродинамические модели коэффициентов обратного отражения являются либо приближенно аналитическими, либо эмпирическими [1–3]. Проблема в данном случае связана не только со сложностью и многофакторностью рассеяния волн, но и с отсутствием учета в данных моделях явления возбуждения встречных волн.
Цель настоящей работы представить строгую электродинамическую модель коэффициента обратного отражения в задаче Френеля, полученную благодаря введению встречных волн, и обобщить её на случай зондирования радаром граничащих сред. Под встречной волной будем понимать излучение вторичных источников среды в граничащих средах в строго обратном направлении волне, возбуждающей эти источники.
Этот механизм во многом аналогичен механизму, при котором имеет место обращение волнового фронта [4]. На существование вынужденного излучения среды в сторону источника при наличии границы раздела указано во многих работах, в частности в [5].
Многомодовое распространение волн в граничащих средах
Рассмотрим механизм распространения волн в граничащих средах, учитывающий эффект возбуждения встречных волн. Пусть имеем две среды, разделенные границей, одна с 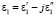 , μ1 = μ0, вторая с
, μ1 = μ0, вторая с 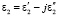 , μ2 = μ0. Предполагаем, что ε1 и ε2 зависят только от частоты. В первой среде расположен радар с антенной, имеющей диаграмму направленности F(?1) (рис. 1).
, μ2 = μ0. Предполагаем, что ε1 и ε2 зависят только от частоты. В первой среде расположен радар с антенной, имеющей диаграмму направленности F(?1) (рис. 1).
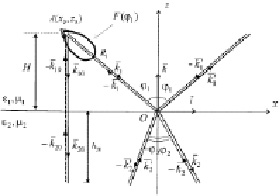
Рис. 1. Прямые и встречные волны в граничащих однородных средах
В соответствии с рис. 1 волна, излученная радаром А, двигается по направлению вектора 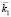 на границу z = 0. В точке О возбуждается отраженная в направлении
на границу z = 0. В точке О возбуждается отраженная в направлении 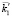 и преломленная с волновым вектором
и преломленная с волновым вектором 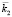 волны. Своим полем преломленная волна возбуждает заряды второй среды, излучение которых образует встречную волну в направлении
волны. Своим полем преломленная волна возбуждает заряды второй среды, излучение которых образует встречную волну в направлении 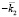 . Волна с
. Волна с 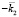 преломляется на границе, образуя обратную волну, поступающую в радар волну с вектором
преломляется на границе, образуя обратную волну, поступающую в радар волну с вектором 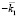 . Мода с
. Мода с 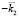 также отражается на границе и образует волну с
также отражается на границе и образует волну с 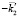 , которая в свою очередь возбуждает встречную волну с
, которая в свою очередь возбуждает встречную волну с 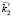 . Последняя преломляясь, распространяется в соответствии с вектором
. Последняя преломляясь, распространяется в соответствии с вектором 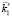 , внося дополнение в зеркальное отражение под углом ?1.
, внося дополнение в зеркальное отражение под углом ?1.
Поскольку диаграмма направленности радара имеет конечную ширину, то при углах облучения ?1 меньших ширины в направлении 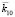 распространяется волна, которая возбуждает отраженную с
распространяется волна, которая возбуждает отраженную с 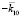 и преломленную с
и преломленную с 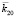 моду. Преломленная волна с
моду. Преломленная волна с 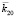 возбуждает встречную моду с волновым вектором
возбуждает встречную моду с волновым вектором 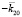 , которая проходит через границу и распространяется с вектором
, которая проходит через границу и распространяется с вектором 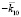 .
.
Отметим также следующее: согласно рис. 1 в граничащих средах возбуждаются прямая и встречная обратная волны с векторами 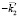 и
и 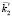 . Мода с
. Мода с 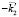 это волна с отрицательным углом преломления, она аналогична волнам, указанным в [6, 7].
это волна с отрицательным углом преломления, она аналогична волнам, указанным в [6, 7].
Заметим также, что из-за наличия границы раздела и при 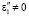 и
и 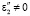 вторичные волны не компенсируются во встречных направлениях к возбуждающим их волнам.
вторичные волны не компенсируются во встречных направлениях к возбуждающим их волнам.
Опираясь на физический механизм, описанный выше, учитывая в решении волновых уравнений наличие встречных волн, определяется многомодовая система собственных мод в граничащих средах [8]. Далее в строгой постановке, решается задача Френеля [9].
В результате установлено, что обратно отраженное поле в граничащих средах, разделенных ровной границей, при облучении её плоской волной из первой среды в предположении, что 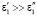 (первая среда практически прозрачна) есть
(первая среда практически прозрачна) есть
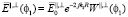 ,
,
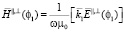 , (1)
, (1)
где
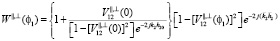 , (2)
, (2)
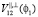 – коэффициенты Френеля,
– коэффициенты Френеля, 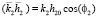 ,
, 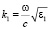 ,
, 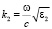 ,
, 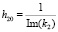 – максимальная глубина проникновения затухающего поля во вторую среду при которой еще возбуждается вторичное излучение,
– максимальная глубина проникновения затухающего поля во вторую среду при которой еще возбуждается вторичное излучение, 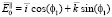 ,
, 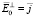 ,
, 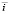 ,
, 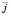
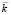 – единичные векторы. Здесь верхним индексом «
– единичные векторы. Здесь верхним индексом « » отмечены величины соответствующие случаю, когда электрический вектор падающей волны лежит в плоскости падения (НН-поляризация); соответственно индексом «
» отмечены величины соответствующие случаю, когда электрический вектор падающей волны лежит в плоскости падения (НН-поляризация); соответственно индексом «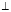 » обозначены величины в случае когда вектор
» обозначены величины в случае когда вектор 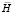 лежит в плоскости падения (VV-поляризация).
лежит в плоскости падения (VV-поляризация).
Множитель (2) и есть коэффициент обратного отражения, этот параметр зависит только от физических свойств среды, частоты излучения и угла падения плоской волны.
Радиозондирование природных сред часто производится с помощью радаров и радиометров. Поэтому необходимо рассчитать обратное поле в точке приема совпадающей с точкой излучения. Кроме того необходимо учесть диаграмму направленности антенны радара (или радиометра) и учесть наличие неровностей границы раздела. В работе эта задача решается следующим образом. Обратное поле в точке наблюдения представляется в виде разложения по плоским волнам, учитывается (1) и направленность излучения источника. Затем применяется векторная формула Грина, согласно которой производится интегрирование по границе раздела сред, в том числе и с учетом неровности. В результате получаем среднее (когерентное) обратное поле в виде:
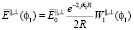 , (3)
, (3)
где
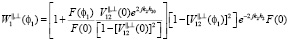 .
.
Входящие в (3) коэффициенты Френеля в случае неровной поверхности раздела следует умножить на 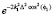 [3, 10, 11], ? – средне квадратичное отклонение неровностей (СКО). Функция
[3, 10, 11], ? – средне квадратичное отклонение неровностей (СКО). Функция 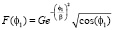 учитывает наличие диаграммы направленности радара, расположенного над наклонной границей раздела сред, G – коэффициент усиления антенны, β – ширина диаграммы направленности, ?1 – угол визирования.
учитывает наличие диаграммы направленности радара, расположенного над наклонной границей раздела сред, G – коэффициент усиления антенны, β – ширина диаграммы направленности, ?1 – угол визирования.
Рассмотрим кратко свойства 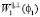 .
.
1. Пусть излучение радара падает нормально на границу раздела. Тогда
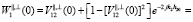
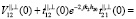
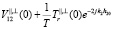 . (4)
. (4)
Здесь 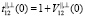 ,
, 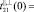
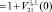 – коэффициенты прохождения волны через границу раздела соответственно из первой среды во вторую и из второй в первую;
– коэффициенты прохождения волны через границу раздела соответственно из первой среды во вторую и из второй в первую; 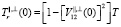 ,
, 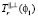 – радиояркостная температура, T – термодинамическая температура среды. Здесь учтено, что
– радиояркостная температура, T – термодинамическая температура среды. Здесь учтено, что 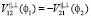 .
.
Из (4) следует, что обратно отраженное поле определяется двумя механизмами: излучением с поверхности раздела и излучением из объема скин-слоя среды, вызванным частью поглощенной энергии, излученной радаром, которая затрачивается на вторичное излучение. Второе слагаемое в (4) подобно тепловому излучению, и соответствует закону Кирхгофа.
Из (4) видно, что если вторая среда хорошо проводящая (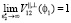 ), то в обратном поле превалирует отражение с поверхности, при этом поле резко уменьшается с ростом ?. В случае если вторая среда диэлектрик, то в обратном отражении существенное значение может иметь составляющая, связанная с объемным излучением.
), то в обратном поле превалирует отражение с поверхности, при этом поле резко уменьшается с ростом ?. В случае если вторая среда диэлектрик, то в обратном отражении существенное значение может иметь составляющая, связанная с объемным излучением.
2. Пусть радар облучает границу под углом близким к скользящему, тогда 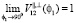 и
и 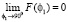 , и из (1) следует что
, и из (1) следует что
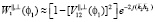 . (5)
. (5)
Обратно отраженное поле в этом случае представляет собой практически только объемное излучение из области скин-слоя. Из (5) видна существенная поляризационная зависимость обратного отражения.
3. Если ?1 > β, то обратное отражение диэлектрической среды больше, чем при проводящей поверхности.
4. Известно, что с увеличением проводимости поверхности угол Брюстера стремится к 90 °, то как следует из (5) будет наблюдаться увеличение обратного отражения 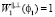 . Этот эффект связан с возбуждением поверхностной обратной волны.
. Этот эффект связан с возбуждением поверхностной обратной волны.
5. Отметим также следующее: если ?1 = 90 °, то 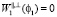 при любых средах и при любых неровностях границы раздела.
при любых средах и при любых неровностях границы раздела.
Особенности, отмеченные выше, не описываются в рамках геометрооптических, оптико-физических и других методов моделирования обратного отражения, в которых не учитывается возбуждение встречных волн.
Согласно (3) эффективная площадь рассеяния границы раздела сред запишем в виде
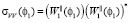 ,
,
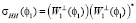 . (6)
. (6)
Если среда представляет из себя слоистую структуру, состоящую из полубесконечного слоя с 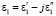 (
(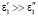 ), слоя толщиной d с
), слоя толщиной d с 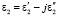 и полубесконечного слоя с
и полубесконечного слоя с 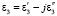 . И если
. И если 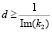 , то коэффициенты обратного отражения вычисляются по (6). Если
, то коэффициенты обратного отражения вычисляются по (6). Если 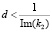 , то коэффициент обратного отражения вычисляются также по (6), но при этом необходимо провести замену
, то коэффициент обратного отражения вычисляются также по (6), но при этом необходимо провести замену 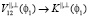 и
и 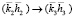 , где
, где
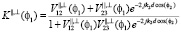 , (7)
, (7)
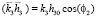 ,
, 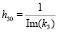 ,
,
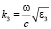 ,
, 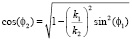 ,
,
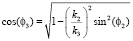 .
.
В работе [3] получены формулы, аналогичные (6). Отличие наших формул заключается в том что (6) получены из строго решения граничной задачи, они пригодны при любых углах падения и для любых ε1, ε2, ε3, они не требуют экспериментальной корректировки. Кроме того в (7) учтена диаграмма направленности антенны.
В обратно отраженном поле присутствует кроссполяризационные компоненты. Их оценка и детальное исследование заслуживает отдельного сообщения
Численные и экспериментальные результаты
В этой части приводится сравнение расчетных по (6) результатов с известными экспериментальными данными по обратному отражению диэлектрических и проводящих сред.
На рис. 2 приведена расчетная и измеренная угловая зависимость коэффициента обратного отражения излучения с частотой f = 94 ГГц в случае сухого асфальта с ε2 = 3,18 – j0,1 и ?0,34×10–3 м.
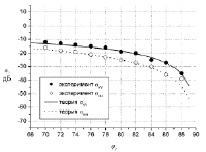
Рис. 2. Угловая зависимость коэффициента обратного рассеяния сухого асфальта
Измеренные данные взяты из [3], расчеты выполнены по (6). Видно хорошее совпадение.
На рис. 3 показаны угловые зависимости коэффициента обратного отражения асфальта (ε2 = 3,1 – j0,1, ?0,34×10–3 м) покрытого слоем воды (εw = 5,6 – j7,8) толщиной 0,46×10–3 м. Измеренные данные взяты также из [3], расчеты выполнены по (7) с учетом (8). Диэлектрическая проницаемость воды рассчитывалась по релаксационной формуле Дебая. Видно хорошее согласие.
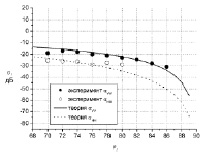
Рис. 3. Угловая зависимость коэффициента обратного рассеяния мокрого асфальтового покрытия
Важные результаты экспериментальных исследований представлены в [12]. Схема эксперимента показана на рис. 4 и 5. Прямоугольные проводящая и диэлектрическая пластины размером 0,6×0,6 м2 облучались полем радара частотой 160 ГГц. Пластины располагались на расстоянии 20 м от источника. Применялась антенна с узкой диаграммой направленности.
На рис. 4 показаны угловые зависимости коэффициента обратного отражения проводящей пластины с СКО неровностей ?3,9×10–6 м.
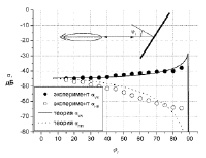
Рис. 4. Угловая зависимость коэффициента обратного рассеяния алюминиевой пластины
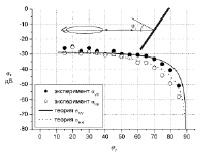
Рис. 5. Угловая зависимость коэффициента обратного рассеяния диэлектрической пластины
На рис. 5 представлены угловые зависимости коэффициента обратного отражения диэлектрической пластины с ε2 = 3,62 – j0,1. СКО неровностей ?7,1×10–6 м. Расчетные зависимости на рис. 4 и 5 получены по (6), экспериментальные результаты взяты из [12]. Диэлектрическая проницаемость металлической пластины вычислялась по формуле Друде. Из рис. 4 и 5 видно хорошее согласие расчетных и измеренных данных.
Из рис. 4 и 5 видно, что в случае проводящей пластины с увеличением угла падения 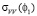 растет достигая максимума при ?1 = ?Б,
растет достигая максимума при ?1 = ?Б, 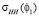 – уменьшается, т.е. имеет место рост поляризационной разницы коэффициентов обратного отражения.
– уменьшается, т.е. имеет место рост поляризационной разницы коэффициентов обратного отражения.
Значение коэффициентов обратного отражения при обеих поляризациях, как следует из рис. 4 и рис. 5 у диэлектрической пластины значительно выше чем у алюминиевой. Этот эффект связан с большим поглощением энергии падающего поля, а значит его большим излучением диэлектрической средой, что соответствует закону Кирхгоффа для теплового излучения.
Заключение
1. Предложен новый метод моделирования обратного отражения на основе многомодового механизма распространения волн в граничащих средах.
2. Показано, что обратное отражение в граничащих сплошных средах представляет собой излучение вторичных источников в виде встречных волн. В рамках макроскопической теории с учетом возбуждения встречных волн в поглощающих средах получено строгое выражение коэффициента обратного отражения для любых углов падения плоской волны на границу раздела сплошных сред.
3. Уставлено, что обратное отражение состоит из двух составляющих: поверхностного (отражение Френеля) и излучение из объема скин-слоя. Указаны диапазоны углов падения при которых превалирует тот или другой механизм. Проведено обобщение формул коэффициентов отражения на случай радиозондирования с помощью радара. Проведено обобщение формул коэффициентов обратного отражения на случай слоистых сред с неровными границами.
4. Проведено сравнение численных расчетов коэффициентов обратного отражения по полученным в работе формулам с экспериментальными данными для сухого асфальта, асфальта покрытого слоем воды, проводящей и диэлектрической пластин конечных размером при углах падения от нулевого до скользящих. Обнаружено хорошее согласие расчетных и экспериментальных данных.
5. Дано объяснение явлению большого значения коэффициента обратного отражения диэлектрической пластины в отличии от проводящей.
Работа выполнена при финансовой поддержке РФФИ, грант № 16-05-00786.

