Простыми числами называют такие натуральные числа, которые делятся только на единицу и само себя. И … других свойств простых чисел до сих пор не найдено. Правда, Евклид доказал, что множество таких чисел – бесконечно, а Эратосфен предложил способ нахождения простых чисел среди натуральных, известный как «решето Эратосфена». Но природа возникновения их так и остается непонятной. Их – то густо, то пусто, и даже сравнивают с сорной травой, которая растет, где хочет и как хочет, не подчиняясь ни какому закону распределения. Гаусс эмпирическим способом обнаружил, что соотношение вида:
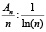 ,
,
где An – число простых чисел, меньших n, стремится к 1 при возрастании n. По сути, математики, отчаявшись найти формулу простых чисел, переключились на исследование распределения их в «среднем». Институт математики Клэя (США) даже в качестве одной из семи математических проблем третьего тысячелетия выдвинул вопрос о гипотезе Римана о количестве простых чисел. «В итоге можно сказать, что поиски элементарных формул, дающих только простые числа, оказались тщетными. Ещё менее обнадеживающей следует считать задачу нахождения такой формулы, которая давала бы только простые числа и при том все простые числа» [1, с. 54].
Однако существует способ вычисления простых чисел, основанный на общеизвестном свойстве, которое гласит: если числа B и C не содержат общих множителей, то число A = B + C будет простым по отношению к ним. Это свойство можно записать в более общем виде: А = |В ± С|, замена знака «+» на «±» не изменяет этого свойства и, если число С превосходит число В, то рассматривается абсолютная величина. Теперь дадим более точную формулировку: «если числа В и С не содержат общих множителей, то числа вида А = |В ± С| являются простыми по отношению ко всем множителям, входящим как в число В, так и в число С». Поэтому, если нам известны первые n простых чисел P1, …, Pn, то, представив число В в виде произведения некоторых из них, а число С как произведение остальных, тогда числа указанного вида будут простыми, при условии, что А < (Pn+2)2. Возьмем пять первых простых числа 1, 2, 3, 5, 7 – тогда: |1×2×3×5 ± 7| = 37; 23 – простые; |3×7 ± 2×5| = 31; 11 также простые и т.д. Ограничение предназначено для исключения случаев, когда в результате вычислений получаются составные числа, содержащие множители, превосходящие Pn. Например, |2×3×5×7 ± 1| = 211; 209, но число 209 = 11×19 является составным.
Рассмотренный способ можно комбинировать с методом проверки, т.е. в вычислениях использовать только часть первых простых чисел, а результаты проверять на наличие в них, в качестве множителей, неиспользуемых простых чисел. Например, |2×5×7 ± 1| = 71; 69, 71 – простое, а 69 из рассмотрения исключается, т.к. содержит в качестве множителя простое число 3.
Обратив особое внимание на то, что в свойстве говорится только о том, что числа В и С не должны содержать одинаковых множителей, приходим к выводу: в представлении числа В любой множитель может входить многократно, это же относится и к числу С, т.е. их можно представлять в виде:
B = Pia×…×Pjb, C = Pkc×…×Pld,
где a, b, c, d – натуральные числа. Например, |2×2×2×2×3×3 ± 5×7| = 107;37 – число 107, хотя и является простым, из рассмотрения исключается в связи с ограничением.
Теперь, если найдены числа вида |Pia×…×Pjb ± 1|, которые удовлетворяют указанному условию и не содержат множителей, не входящих в это представление, то такие числа называют простыми числами-близнецами, если вида | Pia×…×Pjb ± 2|, то – двоюродными простыми числами, |Pia ×…×Pjb ± 3| – троюродными и т.д.
Фактически это объясняет природу простых чисел, которые появляются не сами по себе, а все предыдущие порождают последующие. Тем самым снимается актуальность проблемы поиска закона их распределения, ведь мало кого интересует вопрос о количестве чисел Фибоначчи, не превосходящих определенное число, т.к. есть формула их вычисления. Определенным недостатком рассмотренного способа является то, что при увеличении количества используемых первых простых чисел существенно возрастает объем вычислений, к тому же многие простые числа можно получать различными комбинациями.
Формула, используемая в вычислениях, позволяет обнаружить новое свойство простых чисел, которое можно со всей смелостью назвать аналогом «крылатой» фразы – «все люди братья», т.е. все простые числа в той или иной степени являются братьями.

