В истории Земли известны, по крайней мере, пять периодов катастрофических вымираний живых существ [4, 5, 7, 8], один из которых относится ко времени около 65 млн лет назад и связан с исчезновением динозавров. Учеными высказывались гипотезы и предположения о причинах вымирания, однако до настоящего времени ни одна из гипотез не является всеобъемлющей. В настоящей статье обосновывается связь периода вымирания с циклом сжатия Земли.
Периоды массовых вымираний и возможные циклы сжатия Земли
За последние 500 млн лет произошло по крайней мере пять массовых вымираний – периодов глобальных катастроф в истории Земли, в которые скорость вымирания была намного больше обычной [4]. События происходили 200, 245, 360 и 420 млн лет назад (рис. 1).

Рис. 1. Периоды массовых вымираний на Земле: периоды вымираний обозначены стрелками
65 млн лет назад с лица Земли исчезло 250 видов ящеров, некоторые из которых имели массу 30 тонн. По геологическим меркам это произошло быстро. В результате была уничтожена шестая часть всех видов. Истинные причины массовых вымираний до сих пор не установлены, хотя на этот счет имеются гипотезы и теории.
Не подлежит сомнению, что циклические изменения газового состава атмосферы неизбежно могли повлечь за собой перемены в животном мире. В пользу этой гипотезы имеется немало доводов. Об ее справедливости свидетельствуют анализ скелетных тканей вымерших организмов, закономерности эволюции дыхательного аппарата и системы кровообращения древних животных, характер биохимического режима тканей и особенности эмбрионального развития представителей современного животного мира [7, 8, 9]. Но и эта гипотеза ни в коей мере не может считаться всеобъемлющей.
Бесспорно, что на вымирание организмов определенное влияние оказали и борьба за существование, и местные похолодания, и образование новых горных хребтов, и изменения режима водоемов. Но какую роль сыграл каждый из этих факторов – пока остается невыясненным.
В 1979 г. лауреат Нобелевской премии профессор Луис Альварес и группа ученых Калифорнийского университета изучали в Италии химический состав горных пород, сформировавшихся в конце мелового и в начале палеогенового периодов. В отложениях, разделяющих мезозойские и кайнозойские образования (66 млн лет назад), они обнаружили повышенную концентрацию редких химических элементов. Особенно интересным оказался пласт розоватого известняка, в нижней части которого содержались остатки микроорганизмов мелового, а в верхней части – палеогенового возврата [5].
Между этими палеонтологически охарактеризованными слоями располагался тонкий (не более 1 см) прослой глины, в котором было установлено аномально высокое содержание иридия. Количество этого металла в глинистом прослое более чем в 30 раз превышало его содержание в окружающем известняке.
Известно, что иридий мало распространен в земных породах, но довольно часто встречается в космической пыли и в некоторых типах метеоритов. Поэтому Альварес объяснил эту аномалию как результат столкновения Земли с каким-то космическим телом.
В последующие годы геохимические исследования пограничных отложений мела и палеогена были проведены во многих странах. И в десятках мест удалось установить наличие аномального слоя с повышенным содержанием иридия (в 160 раз выше, чем в окружающих породах) [5].
Стало очевидно, что аномалии иридия имеют глобальный характер и, скорее всего, являются следствием космических причин. Такой причиной могло быть падение на Землю крупного метеорита или астероида. Можно даже приблизительно оценить его размеры – около 10 км в диаметре. Статистические расчеты показывают, что встреча с метеоритом такого размера вероятна один раз в 30–100 млн лет. Энергия подобного удара столь велика, что метеорит неизбежно разрушится. Значительная часть его должна при этом превратиться в пыль, которая вследствие движения воздушных потоков равномерно распределится в атмосфере и на некоторое время может существенно уменьшить ее прозрачность. Естественно, что пока эта пылевая завеса полностью не осядет на земную поверхность, животные и растения будут испытывать некоторую нехватку солнечного света и тепловой энергии. Если же атмосфера окажется настолько насыщенной пылью, что станет почти непрозрачной, то это может привести к гибели определенной части органического мира планеты. Эти аргументы и привел Альварес для объяснения причины вымирания динозавров.
Палеонтологические данные, однако, неопровержимо говорят о том, что вымирание динозавров началось задолго до предполагаемого момента падения астероида и не могло быть его следствием. Да и кратер от упавшего в это время космического тела пока достоверно не найден [5, 7, 8].
Таким образом, перечисленные гипотезы вымирания динозавров не дали однозначного ответа на вопрос о причинах вымираний. В этой связи интерес представляет идея о возможном влиянии динамических и геометрических параметров Земли на предельные размеры животных, на жизнедеятельность живых существ.
Объяснений экстремально больших размеров доисторических животных (архелонов, динозавров-зауроподов, мегатериев и проч.) до сих пор нет. Гигантизм не согласуется с широко применяющимся в современной биомеханике законом квадрата-куба Галилея [3]: когда объект подвергается пропорциональному увеличению размеров, его новый объём v2 будет пропорционален кубу множителя, а новая площадь его поверхности пропорциональна квадрату множителя:
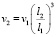 ;
; 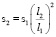 , (1)
, (1)
где v1, l1 – первоначальный объем и первоначальный характерный размер,
v2, l2 – объем и размер после пропорционального увеличения размеров,
s1, s2 – соответственно площади поверхности до и после пропорционального увеличения размеров.
В частности, увеличение размеров животного значительно превзойдет рост его мускульной силы, так как поперечное сечение его мускулов увеличится пропорционально квадрату коэффициента масштабирования, в то время как его масса увеличится пропорционально кубу коэффициента масштабирования. В результате этого сердечно-сосудистые функции сильно ограничатся. Предполагается, что в соответствии с контракционной гипотезой, заключающейся в уменьшении объёма Земли при её охлаждении, гибель динозавров совпала с резким скачком в изменении диаметра Земли. Данная гипотеза представляет интерес для нашего исследования ввиду того, что среднее давление pср, оказываемое весом больших животных Fn на их опорные ступни общей площадью Sоп, в современных условиях было бы неприемлемо разрушительным [10]
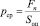 .
.
Логично предположить, что в доисторическую эпоху ускорение свободного падения имело меньшее значение. Как известно, g прямо пропорционально гравитационной постоянной G и обратно пропорционально радиусу Земли. Соответственно, можно предположить, что в период проживания динозавров радиус Земли был больше, а ускорение свободного падения меньше, что позволяло им при их больших размерах существовать без риска повредить свои кости, мышцы, сухожилия и сосуды.
Контракционная гипотеза была предложена в 1829 году Жаном-Батистом Эли де Бомоном для объяснения процессов горообразования Земли [7]. Полное изложение контракционной гипотезы и объяснение в её рамках процессов горообразования Эли де Бомон сделал в труде «Заметки о горных системах», изданном в 1852 году.
Контракционная гипотеза учитывала представления Канта и гипотезу Лапласа о происхождении Солнечной системы из вращающейся туманности; в соответствии с этой гипотезой Земля на начальных стадиях своей эволюции была раскалённым расплавленным шаром и земная кора образовалась при охлаждении его поверхности. При дальнейшем охлаждении Земли, сопровождающимся уменьшением её объёма, должна уменьшаться и площадь её поверхности, что, в свою очередь, должно первоначально вызывать появление неровностей – «морщин» на её поверхности [7]. По мере дальнейшего охлаждения и сокращения объёма Земли механические напряжения коры увеличиваются и в момент, когда они достигают предела прочности горных пород «морщин», происходит их поперечное раздробление, в результате которого боковое давление выжимает складки и каждый поднятый сегмент образует горную систему; в центральную, наиболее ослабленную дроблением область горной системы затем внедряются из глубин магматические массы.
Контракционная гипотеза объясняла зональность горных массивов и повторяемость эпизодов горообразования по мере дальнейшего сжатия, сопровождающегося повторным ростом механических напряжений в коре. Эли де Бомон связал эти эпизоды со сменами ископаемых фаун и флор в рамках эволюционной теории катастроф Жоржа Кювье. Анализируя расположение горных систем, де Бомон пришёл к выводу, что горные системы отвечают большим кругам земного шара, а распределение горных систем привязано к 15 большим кругам, соответствующим рёбрам вписанного в земной шар икосаэдра.
В основу гипотезы легла аналогия с печёным яблоком, которое за счёт усыхания покрывается множеством морщин. Создатели гипотезы полагали, что складчатые системы на Земле аналогичны таким морщинам.
С самого своего появления контракционная теория подверглась жёсткой критике. Однако внутренняя логичность гипотезы и трудности альтернативных теорий позволили ей очень долго быть одной из основных геодинамических концепций.
В различных формах контракционная гипотеза участвовала в разновидностях теории геосинклиналей. Теория геосинклиналей предполагала, что развитие складчатой области начинается с образования прогиба, в котором накапливается большой объём осадков, а затем прогиб сжимается и происходит горообразование. Контракционная гипотеза объясняла эту последовательность событий тем, что за счёт уменьшения объёма Земли её поверхность лопается (происходит растяжение с образованием прогиба), а затем, при последующем уменьшении объёма, место разрыва оказывается самым слабым и именно в этом месте образуется складчатость. Таким образом, контракционная теория и концепция геосинклиналей взаимно дополняли друг друга и стали базовым представлением о земных геологических процессах [7].
Анализ механических и динамических параметров живых организмов
Одним из важных механических параметров, который оказывает влияние на жизнедеятельность животных, является давление на грунт. В табл. 1 приведены результаты расчета давления на грунт для некоторых видов динозавров и современных животных, при этом ускорение свободного падения принято 9,8 м/с2.
Учитывая, что предельное недеформирующее давление на грунт составляет 50–100 кПа, давление со стороны динозавров, приведенное в табл. 1, представляется неприемлемым для нормального передвижения.
Таблица 1
Давление на грунт для некоторых видов динозавров и современных животных
|
Вид |
Масса, М, т |
Опорная поверхность, Sоп, м2 |
Давление, p = Mg/S, кПа |
|
Апатозавр |
35,0 |
1,2 |
290,0 |
|
Тираннозавр |
7,0 |
0,6 |
120,0 |
|
Игуанодон |
5,0 |
0,4 |
120,0 |
|
Африканский слон |
4,5 |
0,6 |
70,0 |
|
Крупный рогатый скот |
0,3 |
0,04 |
75 |
|
Человек |
0,07 |
0,035 |
20 |
Давление со стороны апатозавра, строение тела которого принципиально сходно со строением современного африканского слона, превышает давление со стороны африканского слона более чем в 4 раза.
Для периода проживания динозавров выполним оценку допустимого ускорения свободного падения. Исходим из того, что они не должны были проваливаться в мягкий грунт с несущей способностью 100 кПа. Для этого используем уравнение p = Mg/S [10] и данные табл. 1. Получим следующие значения ускорения: для апатозавра g = M/(pS) = 3,43 м/с2; для тираннозавра g = 8,57 м/с2; для игуанодона g = 8 м/с2. Среднее арифметическое значение ускорения g = 6,6 м/с2.
Современные танки, которые сопоставимы по массе с самыми крупными динозаврами, создают давление на грунт примерно 93,87 кПа. При этом давление на грунт от движущегося танка остаётся примерно постоянным, а давление от ходьбы динозавра, перемещающего вес тела с одной ноги на другую, как минимум вдвое больше давления, указанного в табл. 1. Например, у апатозавра пиковое давление на грунт может достигать 580 кПа и более. Давление на грунт характеризует риск для животного или техники увязнуть во влажном грунте.
Очевидно, что существующие сегодня крупные животные, такие как слоны, жирафы, определяют предел допустимых нагрузок на грунт для нормальной жизнедеятельности в современном мире размеров.
Такого рода гигантизм противоречит применяемому в биомеханике закону квадрата-куба и ставит перед современной наукой множество вопросов, которые до сих пор остаются без ясных ответов. В частности, химический состав костей динозавров по современным данным эквивалентен костям ныне существующих животных (Ca10[PO4][OH]2). Важность этого в том, что химические связи элементов определяют такие свойства материала, как прочность и плотность. Таким образом, маловероятно для костей динозавров и птерозавров быть легче или сильнее, чем кости рептилий и млекопитающих сегодняшних дней, а им приходилось выдерживать колоссальную нагрузку со стороны их тел.
Ископаемые следы, как правило, отражают передвижение динозавров в спокойном состоянии. Отдельный интерес представляет способность динозавров к быстрому бегу в экстремальной ситуации, прыжкам, резкому маневрированию. Обо всём этом можно косвенно судить по прочности костей к динамическим нагрузкам.
Во всех оценках, приведенных выше, все параметры Земли приняты современными – в том числе, ускорение свободного падения, плотность атмосферы и атмосферное давление.
В дальнейших расчетах мы примем максимально допустимыми параметры максимально большого современного животного – африканского слона, т.е. будем рассматривать его размер как предельно допустимый в современных условиях.
Оценка давления на опорно-двигательную систему динозавров
Кость, как и любой другой материал, имеет предельные значения напряжений растяжения и сжатия, достижение которых ведет к разрушению конструкции (табл. 2).
Таблица 2
Предельная прочность некоторых материалов
|
Наименование параметра |
Сталь |
Бетон |
Кость конечности |
|
Предельная прочность на растяжение, МПа |
500 |
2 |
130 |
|
Предельная прочность на сжатие, МПа |
500 |
20 |
170 |
Результаты вычислений значений давлений на кости некоторых млекопитающих приведены в табл. 3.
Таблица 3
Давление на кости в спокойном состоянии некоторых млекопитающих
|
Млекопитающее |
Длина окружности передних ног, мм |
Длина окружности задних ног, мм |
Приблизительная общая площадь кости, мм2 |
Вес животного, Н |
Давление в момент стояния, кПа |
|
Луговая мышь |
5 |
5 |
4 |
0,5 |
100 |
|
Морская свинка |
10 |
15 |
29 |
3,8 |
130 |
|
Серая белка |
10 |
13 |
24 |
3,9 |
160 |
|
Серая лисица |
28 |
26 |
130 |
39 |
300 |
|
Енот |
30 |
28 |
150 |
50 |
330 |
|
Пятнистый леопард |
45 |
41 |
330 |
140 |
420 |
|
Волк |
62 |
62 |
680 |
470 |
690 |
|
Лев |
104 |
94 |
1700 |
1400 |
810 |
|
Полярный медведь |
158 |
135 |
3820 |
4390 |
1150 |
|
Слон |
459 |
413 |
33700 |
57800 |
1710 |
График зависимости давления на кости животного от его веса представлен на рис. 2.
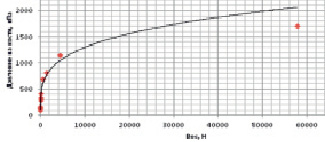
Рис. 2. Зависимость давления на кости от веса животного
Полученная зависимость интерполируется степенной функцией вида y = 113,37x0,2647. С её помощью легко оценить оказываемое на кости динозавров давление (табл. 4).
Таблица 4
Интерполяция давления на кости динозавров
|
Название |
Вес, т |
Давление на кости, кПа |
|
Аргентинозавр (Argentinosaurus huinculensis) |
73 |
4041 |
|
Пуэртазавр (Puertasaurus reuili) |
70 |
3997 |
|
Аламозавр (Alamosaurus sanjuanensis) |
70 |
3997 |
|
Футалогнкозавр (Futalognkosaurus dukei) |
60 |
3837 |
|
Завропосейдон (Sauroposeidon proteles) |
60 |
3837 |
|
Паралититан (Paralititan stromeri) |
59 |
3820 |
|
Туриазавр (Turiasaurus riodevensis) |
48 |
3617 |
Учитывая, что динамические нагрузки превышают статические в 1,5–3 раза, можно предположить, что возможное давление на кости приведенных динозавров достигало 12 МПа, что значительно превышает предельное давление на кости (1,7 МПа), оказываемое слоном при его движении.
Выше проведенные исследования показывают, что величина ускорения свободного падения в период существования динозавров не могла быть равной современному его значению. Допуская, что динамические условия на Земле в период Мезозойской эры не совпадали с современными условиями и эти условия позволяли животным гигантских размеров нормально выживать, выполним сравнение периодов колебаний тел животных в зависимости от их размеров и ускорения свободного падения на Земле.
Одним из ключевых параметров живых организмов, наряду с рассмотренным давлением, является средняя частота собственных колебаний. Колебания конструкции описываются известным дифференциальным уравнением
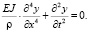 (2)
(2)
В результате решения уравнения (2) получается формула для периода колебаний [1]:
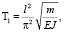 (3)
(3)
где l – длина нижних конечностей, м; m – масса тела животного, кг;
Е – модуль упругости, Н/м2; J – момент инерции тела, м4.
Для оценочных расчетов формулу (3) можно привести к более удобному виду
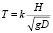 , (4)
, (4)
где D – характерный размер тела по направлениям осей Х (вдоль тела) и У (поперек тела), м;
H – высота, м; k – коэффициент для каркасной конструкции, равный 0,43;
g – ускорение свободного падения, м/с2.
Формула (4) широко используется в прочностных расчетах инженерных конструкций. Живой организм имеет скелет, следовательно, его можно представить как каркасную конструкцию. В этом случае представляется возможным использовать полученную формулу для вычисления периода его колебаний.
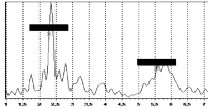
Авторами проведен эксперимент, в ходе которого был получен частотный спектр колебаний человека. Эксперименты выполнялись с помощью комплекса для динамических испытаний «Струна-Стрела» [1] с применением пьезокерамических акселерометров типа А1638 в частотном диапазоне от 0,1 до 400 Гц. Общий вид приборов контроля, использованных в эксперименте, показан на рис. 3, а спектры колебаний – на рис. 4 и рис. 5.
|
|
|
|
Рис. 3. Приборный комплекс для динамических испытаний человека |
Рис. 4. Спектр вертикальных колебаний в диапазоне от 1 до 7 Гц |
|
|
|
|
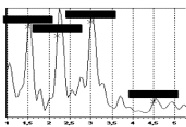
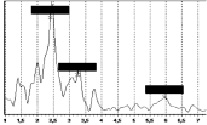
Рис. 5. Спектры поперечных (слева) и продольных (справа) колебаний в диапазоне от 1 до 7 Гц |
|
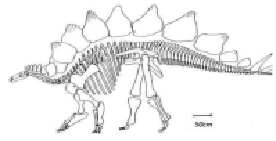
Рис. 6. Продольный разрез скелета динозавра Tuojiangosaurus: H = 3,88 м; Y = 1,5 м; Х = 7,22 м
Эксперимент показал, что основная доля частот лежит в пределах от 2 до 3 Гц. Результаты расчета периода и частоты продольных колебаний для животного (D = 0,4 м; Н = 1,6 м) показали, что период колебаний оценивается величиной 0,277 с, а частота – 3,61 Гц. Эти результаты хорошо согласуются с полученными экспериментальными данными, что позволяет допустить применение формулы (4) для оценки колебаний живых организмов в состоянии покоя.
Оценка периода колебаний тела крупного динозавра
Рассмотрим период колебаний тела конкретного динозавра в состоянии покоя, приняв за основу формулу (4). На рис. 6 представлен продольный разрез скелета динозавра Tuojiangosaurus и масштабный отрезок, равный 0,5 м.
Подставляем исходные данные (H, Y, X) в формулу (4) и вычисляем значения характеристик для живых организмов, результаты заносим в табл. 4.
Таблица 4
Периоды колебаний животных
|
№ п/п |
Биологические объекты |
Тх/[Тх]* |
Тy/[Тy] |
|
1 |
Человек |
0,3/0,276 |
0,4/0,45 |
|
2 |
Африканский слон |
–/0,249 |
–/0,46 |
|
3 |
Динозавр Tuojiangosaurus |
–/0,157 |
–/0,346 |
Примечание. *В числителе – расчетное значение, в знаменателе – экспериментальное.
Полученный результат более чем в полтора раза превышает средний период колебаний современных животных с аналогичными пропорциями тела.
Оценим величину ускорения свободного падения, при котором конструкция живого организма не разрушится. Для этого в формулу (5) подставим исходные данные, принимая значение параметра Ту в пределах 0,45 с (жесткое тело), тогда получим g = 5,8 м/с2.
Таким образом, оценки g с использованием трех независимых подходов дают близкие величины g = 5,8…6,6 ≈ 6,2 м/с2, что значительно меньше величины g = 9,8 м/с2 и в соответствии с теорией прочности скелет рассматриваемого динозавра в условиях современной гравитации близок к разрушению. Полученный результат согласуется с гипотезой сжимающейся Земли, поскольку для достижения такого g потребуется радиус Земли вдвое меньше современного.
Оценка параметров Земли на основе данных о давлении на грунт
В табл. 1 приведены значения давления на грунт для некоторых видов животных. В частности, было показано, что давление со стороны таких крупных животных, как апатозавр, более чем в два раза превышает предельное недеформирующее давление на грунт, равное в среднем 100 кПа. Проведем оценку ускорения свободного падения исходя из предположения, что динозавры не увязали во влажном грунте (что необходимо для нормальной жизнедеятельности). Для этого решаем неравенство
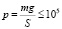 ,
,
где m – масса животного.
Подставляя параметры апатозавра (m = 35 т, S = 1,2 м2), получаем верхнюю оценку ускорения свободного падения:
g ≤ 3,428 м/с2.
Определим радиус Земли, используя закон всемирного тяготения и ускорение свободного падения, принимая полученные выше значения g1 = 3,428 м/с2 и g2 = 6,6 м/с2:
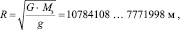
где G – гравитационная постоянная, G = 6,673?10-11 Нм2/кг-2; Мз – масса Земли, кг.
Таким образом, по нашему мнению, одной из главных причин массового вымирания динозавров явилось уменьшение радиуса Земли, вследствие которого произошло увеличение значения ускорения свободного падения.