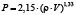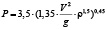Расчет нагрузки селевого потока на противоселевые сооружения является важным этапом при проектировании защитных сооружений. Но данный этап осложняется большим разнообразием существующих формул. Такое разнообразие формул является следствием не только сложностью самой природы оползней и селевых потоков в горных районах страны, но и сложностью выбора модели воздействия грязевых потоков на противоселевые сооружения. Большинство исследователей предлагают формулы расчета на основе гидродинамической модели воздействия селевых потоков на противоселевые сооружения. Но все уравнения гидродинамики основаны на свойствах бесконечного потока в то время как горные паводки и селевые потоки являются относительно кратковременными явлениями длительностью от пяти до получаса. По характеру воздействия селевым потокам близка волновая модель гидравлического удара.
Цель исследования
На основе экспериментальных исследований в данной статье обосновывается ударно волновая модель воздействия на противоселевые сооружения и приводится оценка верхнего предела нагрузки селевого потока.
Материалы и методы исследования
Для расчета нагрузки селевого потока исследователями предложены в основном четыре модели воздействия селевого потока на преграду:
– гидростатическая модель;
– гидродинамическая модель;
– комбинированная модель гидростатического и гидродинамического воздействия;
– волновая модель гидравлического удара.
Формула расчета пиковой нагрузки селевого потока на преграду на основе гидростатической модели предложены Лихтенханом (1973), Арманини (1997), Скоттон и Деганутти (1997)
рpeak = k·ρ·g·h
где ppeak – пиковая нагрузка селевого потока, k – эмпирический коэффициент, ρ – плотность селя, h – высота потока. Эмпирический коэффициент k предложено Лихтенханом (1973) в интервале 2,8–4,4. Арманини предложил этот коэффициент взять равным 5. Скоттон и Деганутти предложили эмпирический коэффициент взять в интервале 2,5–7,5 [6].
В основу расчета нагрузки от селя многими исследователями берутся принцип гидродинамическое давления обтекания преграды струей. Этот принцип положен в основу вывода формул С.М. Амирджанова, У.Р. Мирза-заде [1], Г.М. Беручашвили, Херхеулидзе, Сохадзе и других исследователей.
Приведем известные формулы расчета нагрузки селя на поперечную глухую преграду в виде табл. 1.
В формуле расчета ГрузНИИГиМ коэффициент K определен экспериментально на лабораторной установке в диапазоне изменения скоростей течения селя от 1,5 до 4,3 м/с, глубин потока от 4 до 10 см. Суммарное давление селя на плоский щит (преграду высотой 30 см) измерялось динамометром и тензодагчиками.
Таблица 1
Формулы расчета давления
|
ГрузНИИГиМ |
|
|
Ржевский Б.Н., Нечаев Н.Ф. |
|
|
Херхеулидзе И.И. |
|
Примечания. ρ – плотность селя, кг/м3; V – скорость селя, м/с.
Приведем сравнительные графики этих формул рис. 1.
В основу формулы расчета зарубежных авторов, на основе гидродинамической модели, положена формула
Рpeak = a·ρ·V2
где эмпирический коэффициент «a» зависит от режима движения потока [6]. Все основные значения данного коэффициента, предложенные различными исследователями, сведены в табл. 2.
Хиублем и Холцинерем предложены формулы расчета на основе комбинированной модели гидростатического и гидродинамического воздействия
pmax = 5·ρ·ν 0,8(g·h)0,6
По волновой модели гидравлического удара была предложена Гонором А.Л. и Пик-Пичаком Е.Г. [3] следующая формула расчета:
P = a·ρ·c·V
где ρ – плотность селя, кг/м3; V – скорость селя, м/с; α – процентное содержание воздуха в водонасыщенном грунте, меняется в пределах 0÷0,04.
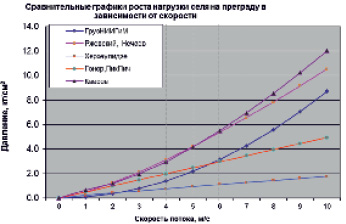
Рис. 1. Сравнительные графики давления селя в зависимости от скорости
Таблица 2
Эмпирические коэффициенты зарубежных авторов
|
Исследователи |
год |
Эмпирический коэффициент a |
Примечание |
|
VanDine |
1996 |
1,5A |
Вводится площадь сечения A |
|
Watanabe и Ike |
1981 |
4,0 |
Гранулированный ламинарный поток |
|
Zhang |
1993 |
6,0–10,0 |
На основе натурных замеров |
|
Egli |
2005 |
4,0 |
Крупнообломочный материал |
|
Wendeler |
2008 |
1,4–4,0 |
Воздействия на нежесткие податливые преграды |
|
Bugnion и др. |
2011 |
0,8–1,6 |
Натурные эксперименты на склоне холма |
Таблица 3
Модели воздействия селевого потока на жесткую преграду
|
Модель воздействия селевого потока |
Особенность воздействия |
Режим воздействия |
|
Гидростатическая |
Селевая масса покоится и величина воздействия зависит от высоты и плотности |
Установившаяся, равновесно-статическая. |
|
Гидродинамическая |
Селевая масса движется и величина воздействия зависит от скорости и плотности |
Установившаяся, равновесно-динамическая. |
|
Волновая модель |
Селевая масса движется и величина воздействия зависит от скорости и массы потока |
Импульсная, неравновесная |
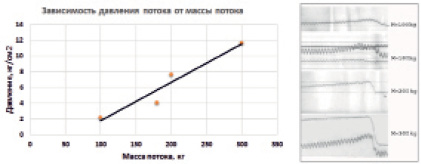
Рис. 2. График изменения давления потока в зависимости от массы
Как видим эмпирические коэффициенты в приведенных формулах меняются в значительных пределах. Данные значения получены в лабораторных условиях. Недостаточно обоснованы перенос этих значении на натурные масштабы. В этих формулах фигурируют только два параметра, это скорость и плотность селевого потока, т.е. давление выражается в виде P = f(ρ, V). На наш взгляд значения этих формул недостаточно отражают реальные давления, оказываемые селевыми потоками на преграды. Как известно, ранее приведенные формулы обоснованы на известной формуле гидравлического обтекания тела потоком.
Рассмотрение моделей воздействия селевого потока на на поперечную жесткую преграду показывает что основная часть исследователей не считают воздействие селевого потока на преграду процессом ударного воздействия. Так как большинство предлагаемых расчетных формул основаны на гидродинамической модели воздействия. Рассмотрим основные особенности гидростатической, гидродинамической и ударно-волновой модели воздействия селевого потока на поперечную жесткую преграду (смотрите табл. 3).
Таким образом из таблицы видно основные отличия гидродинамической модели от ударно-волновой модели. По гидродимической модели воздействия не имеют значения длина, объем, масса потока. Между потоком и преградой устанавливаются равновесное состояние и величина воздействия пропорцианально квадрату скорости. На наш взгляд данная модель подходить только для сквозных противоселевых сооружений. Так как именно в этом случае происходит обтекание преграды потоком. По ударно волновой модели воздействия величина воздействия пропорцианально первой степени скорости потока и зависит от массы потока вовлеченную в начальной стадий ударного воздействия потока.
Селевые потоки 1973 г. на р. М. Алматинка, 1975 и 1977 гг. на р. Б. Алматинка показали, что проблема динамического воздействия селя на преграду значительно сложнее, чем представляется теоретически. В 1977 г. на р. Б. Алматинка селем были разрушены опоры ЛЭП, водозаборы каскада ГЭС, кирпичные дома, причем нагрузки, которые способны были выдерживать эти разрушенные сооружения, в несколько раз превышали давления, подсчитанные по общеизвестным формулам обтекания. Ясно что, причиной разрушения этих сооружений явились импульсные нагрузки.
Результаты проведенных нами экспериментальных исследований в лабораторных условиях [2] показали зависимость нагрузки селя от массы потока (смотрите рис. 2).
Также было выявлено, что максимальная нагрузка от удара селевого потока приходится на первые 50÷100 мсек времени воздействия потока. Учитывая высокую вязкость селевой массы необходимо констатировать большую погрешность модели обтекания тела потоком т.к. за короткое время удара сель не успевает изменить форму.
Результаты исследования и их обсуждение
Как мы видим, давление возрастает примерно пропорционально относительно массы. При волновом процессе удара волна возмущений распространяется со скоростью звука от передней части селя на заднею часть. Таким образом, процесс нарастания давления, а также длительность воздействия селя является сложным процессом, который зависит как от скорости самого потока, так и от скорости распространения фронта возмущений внутри селевого потока. Также на характер воздействия потока на препятствие влияет скорость распространения возмущения внутри селя. Скорость звука внутри селя определяется физическими свойствами селевой массы. Как известно скорость звука в жидкостях определяется по формуле:
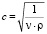
где ν – коэффициент сжимаемости жидкости, ρ – плотность жидкости.
Так как сель является многокомпонентной средой, то сжимаемость селя определяется не только водой, но и другими компонентами. Также на сжимаемость селя влияет содержание воздуха и других газов. Влияние воздухосодержания на свойства водонасыщенного грунта не ограничивается увеличением или снижением его сжимаемости. Исследованиями Г.М. Ляхова [4] показана, что максимальное давление, скорость распространения максимума давления и другие параметры, волны существенно зависят от содержания воздуха α1 в водонасыщенном грунте. С возрастанием α1 от нуля до 0,04 максимальное давление убывает на два порядка, скорость максимума – более чем на порядок. При изменениях содержания воздуха α1 от 0 до 0,01 а, скорость звука с в водонасыщенном грунте изменяется от 1620 до 26 м/с.
Приближенно оценить влияние воздухонасыщения на величину пиковых (ударных) нагрузок от селя на жесткое сооружение можно следующим образом:
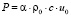 .
.
А.Л. Гонор и Е.Г. Пик-Пичак [3] отмечают, что максимальные пиковые нагрузки от снежных лавин на твердую стенку находятся в хорошем соответствии с расчетом по одномерной теории гидравлического удара, где α ≤ 1 – процентное содержание воздуха в водонасыщенном грунте (сель), меняется в пределах 0÷0,04; ρ0 – плотность жидкости; с – скорость распространения ударной волны; u0 – скорость соударения жидкости с твердой стенкой.
Здесь важное значение имеет оценка скорости звука в селевой массе. В проведенных нами экспериментах выявленная скорость звука равнялась 146 м/с. Данное значение определялось косвенным методом. По оценкам зарубежных исследователей скорость звука в водонасыщеном грунте находится в интервале 100÷300 м/с [7].
Исходя из этого можно полагать, что график возрастания давлении (рис. 2) ограничено сверху некой эффективной массой, которая определяется как Me = ρ·s·c·Δτ, где ρ – плотность среды, s – площадь поперечного сечения потока, c – скорость звука в среде, Δτ – длительность нарастания пикового давления. По полученным осциллограммам были изучены длительности воздействия потока на стенд датчиков. Длительность нарастания давления от начала удара до максимального значения находилась в пределах 0,03÷0,09 сек в то время как длительность самого удара менялась в пределах 0,32÷0,38 сек. Исходя из положения, что сжимаемость грязекаменной среды сильно зависит от газовой компоненты [5] и по последним оценкам скорость распространения возмущения в среде равно 100 ≤ с ≥ 300 м/c мы можем определить верхний предел давления в полученных нами результатах. Длина распространения ударной волны L = 300 м/с·50·10-3 с = 15 м. Отсюда эффективная масса равно
Me = ρ·s·c·Δτ = 2·103 кг/м3·21× ×10-2 м2·15 м = 6300 кг,
что дает максимально возможное давление при предположении о линейной зависимости возрастания давления от массы в районе 250 кгс/см2.
Выводы
Таким образом мы предлагаем более сложную модель расчета нагрузки селевого потока на преграду. Которую можно представить в виде P = f(ρ, ν, Mе, V), где ρ, ν – плотность и сжимаемость грязекаменной среды, Mе – эффективная масса, которая определяется скоростью распространения звука в потоке и площадью сечения потока. Кинетическая энергия эффективной массы селевого потока гасится в первые секунды удара и в этот момент происходит наибольшая нагрузка на защитные сооружения. Далее воздействие селевого потока постепенно падает до уровня гидростатического давления. Предлагаемая нами модель основана на волновой модели ударного воздействия и позволяет переносить результаты лабораторных исследований на натурные масштабы, что являлось слабым местом предыдущих моделей расчета.


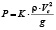 , K = 4,5
, K = 4,5