Для прогноза безопасности сложной системы, находящейся в водной, нефтяной и твердой деформируемой среде, при нестационарных волновых воздействиях применяется численное моделирование.
Волны напряжений различной природы, распространяясь, в деформируемом теле взаимодействуют, друг с другом, что приводит к образованию новых областей возмущений, перераспределению напряжений и деформаций. При интерференции волн напряжений их интенсивности складываются. Они могут достигать значений, превосходящих предел прочности материала. В этом случае наступает разрушение материала.
После трехкратного или четырехкратного прохождения и отражения волн напряжений в теле процесс распространения возмущений становится установившимся, напряжения и деформации усредняются, тело находится в колебательном движении.
Для моделирования волн напряжений в деформируемых областях сложной формы применяется численное моделирование. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при ударных воздействиях на сооружения. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Матрица упругости выражена через скорость продольных волн, скорость поперечных волн и плотность.
Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений. За основные неизвестные приняты два перемещения и две скорости перемещений в узле конечного элемента.
Задачи решаются с методом сквозного счета, без выделения разрывов. Применяется кусочно-линейная аппроксимация для уменьшения влияния разрывов на точность результатов численного решения, полученных с помощью метода конечных элементов в перемещениях.
Линейная динамическая задача с начальными и граничными условиями в виде дифференциальных уравнений в частных производных, для решения задач о нестационарных воздействиях на деформируемые объекты сложной формы, с помощью метода конечных элементов в перемещениях приведена к системе линейных обыкновенных дифференциальных уравнений с начальными условиями, которая решается по явной двухслойной схеме.
Рассмотрим задачу об ударном аварийном выбросе нефти (рис. 3) в сложной системе, которая состоит из следующих деформируемых сред: нефтяная, водная и твердая (рис. 1).
Некоторая информация в области моделирования волн напряжений в сложных деформируемых областях различной формы с помощью рассматриваемого метода приведена в следующих работах [1–10].
В работах [1–10] приведена информация о физической достоверности и математической точности рассматриваемого численного метода, алгоритма и комплекса программ.
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения:
1 кгс/см2 ≈ 0,098 МПа;
1 кгс с2/см4 ≈ 0,98×109 кг/м3.
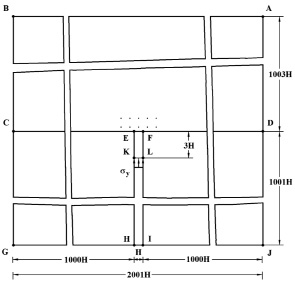
Рис. 1. Постановка задачи об ударном аварийном выбросе нефти в сложной деформируемой системе
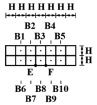
Рис. 2. Точки В1–В10, в которых получены упругие напряжения во времени
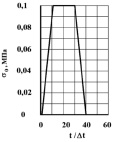
Рис. 3. Ударное воздействие
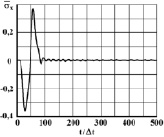
Рис. 4. Изменение упругого нормального напряжения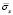 
во времени t/Δt в точке В1
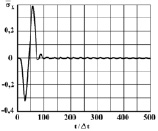
Рис. 5. Изменение упругого нормального напряжения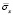 
во времени t/Δt в точке В2
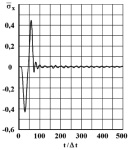
Рис. 6. Изменение упругого нормального напряжения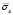 
во времени t/Δt в точке В3
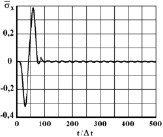
Рис. 7. Изменение упругого нормального напряжения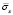 
во времени t/Δt в точке В4
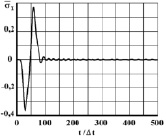
Рис. 8. Изменение упругого нормального напряжения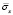 
во времени t/Δt в точке В5
На контуре KL приложено нормальное воздействие σy (рис. 1), которое при 0 ≤ n ≤ 10 (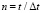
) изменяется линейно от 0 до P, при 11 ≤ n ≤ 30 равно P и при 31 ≤ n ≤ 40 от P до 0 (P = σ0, σ0 = 0,098 МПа ( 1 кгс/см2)). Принято следующее допущение: 1 кгс/см2 ≈ 0,098 МПа.
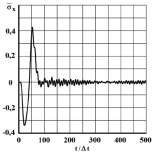
Рис. 9. Изменение упругого нормального напряжения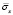 
во времени t/Δt в точке В6
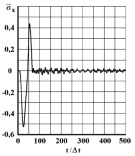
Рис. 10. Изменение упругого нормального напряжения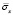 
во времени t/Δt в точке В7
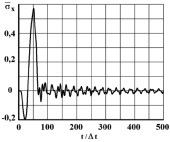
Рис. 11. Изменение упругого нормального напряжения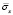 
во времени t/Δt в точке В8
Для твердой деформируемой среды ECGHK и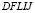 
приняты следующие исходные данные: 
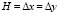; Δt = 1,393×10-6 с; E = 3,09×104 МПа (3,15×105 кгс/см2); ν = 0,2; ρ = 0,25×104 кг/м3 (0,255×10-5 кгс с2/см4); Ср = 3587 м/с; Сs = 2269 м/с. Приняты следующие допущения: 1 кгс/см2 ≈ 0,098 МПа; 1 кгс с2/см4 ≈ 0,98×109 кг/м3.
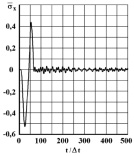
Рис. 12. Изменение упругого нормального напряжения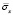 
во времени t/Δt в точке В9
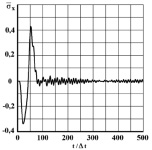
Рис. 13. Изменение упругого нормального напряжения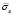 
во времени t/Δt в точке В10
Для водной деформируемой среды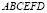 
приняты следующие исходные данные: 
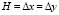; Δt = 3,268×10-6 с; ρ = 1,025×103 кг/м3 (1,045×10-6 кгс с2/см4); Ср = 1530 м/с. Принято следующее допущение: 1 кгс с2/см4 ≈ 0,98×109 кг/м3.
Для нефтяной деформируемой среды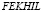 
приняты следующих исходные данные: 
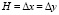; Δt = 3,876×10-5 с; ρ = 0,825×103 кг/м3 (0,841×10-6 кгс с2/см4); Ср = 1290 м/с. Принято следующее допущение: 1 кгс с2/см4 ≈ 0,98×109 кг/м3.
При расчетах принимается минимальный шаг по времени Δt = 1,393×10-6 с.
Исследуемая расчетная область имеет 4014010 узловых точек. Решается система уравнений из 16056040 неизвестных.
На рис. 4–13 показано изменение упругого нормального напряжения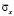 
(
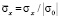) во времени n в точках B1–B10 (рис. 2), находящихся в водной среде.
Полученные результаты можно оценить как первое приближение к решению сложной комплексной задачи об ударном аварийном выбросе нефти в сложной деформируемой системе.