Для прогноза безопасности уникальных сооружений, находящихся в воздушной и твердой деформируемой среде, при волновых воздействиях применяется численное моделирование. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при волновых воздействиях на сооружения. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Матрица упругости выражена через скорость продольных волн, скорость поперечных волн и плотность.
Некоторая информация о моделировании нестационарных упругих волн напряжений в деформируемых областях с помощью рассматриваемого численного метода приведена в следующих работах [1–10].
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ ≈ 0,098 МПа; 1 кгс с2/см4 ≈ 0,98×109 кг/м3.
В работах [1–4, 6–10] приведена информация о физической достоверности и математической точности применяемого численного метода, алгоритма и комплекса программ.
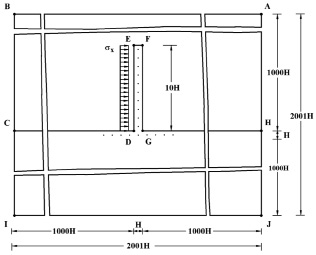
Рис. 1. Постановка задачи о воздействии воздушной ударной волны на консоль с упругой полуплоскостью (соотношение ширины к высоте консоли – один к десяти)
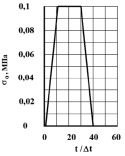
Рис. 2. Ударное воздействие для задачи о воздействии воздушной ударной волны на консоль с упругой полуплоскостью (соотношение ширины к высоте консоли – один к десяти)
Рассмотрим задачу о воздействии воздушной ударной волны (рис. 2) на консоль (соотношение ширины к высоте консоли – один к десяти) с упругой полуплоскостью (рис. 1).
На контуре ED приложено нормальное воздействие σx, которое при 0 ≤ n ≤ 10 (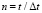
) изменяется от 0 до P, а при 11 ≤ n ≤ 30 равно P и при 31 ≤ n ≤ 40 изменяется от P до 0 (P = σ0, σ0 = 0,098 МПа (1 кгс/см2)). Принято следующее допущение: 1 кгс/см2 ≈ 0,098 МПа. Граничные условия для контура 
при 
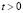
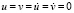. Отраженные волны от контура 
не доходят до исследуемых точек при 0 ≤ n ≤ 50. На границе 
приняты условия непрерывности перемещений.
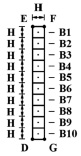
Рис. 3. Точки B1–B10, в которых получены упругие напряжения во времени для задачи о воздействии воздушной ударной волны на консоль с упругой полуплоскостью (соотношение ширины к высоте консоли – один к десяти)
Для воздушной деформируемой среды ABCDEFGH приняты следующие исходные данные: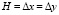 
; ?t = 0,147×10-4 с; Cp = 340 м/с; ρ = 1,2 кг/м3 (1,245×10-9 кгс с2/см4). Принято следующее допущение: 1 кгс с2/см4 ≈ 0,98×109 кг/м3.
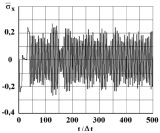
Рис. 4. Изменение упругого нормального напряжения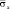 
во времени t/?t в точке B1 (соотношение ширины к высоте консоли – один к десяти)
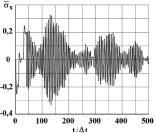
Рис. 5. Изменение упругого нормального напряжения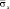 
во времени t/?t в точке B2 (соотношение ширины к высоте консоли – один к десяти)
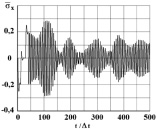
Рис. 6. Изменение упругого нормального напряжения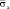 
во времени t/?t в точке B3 (соотношение ширины к высоте консоли – один к десяти)
Для твердой деформируемой среды 
приняты следующие исходные данные: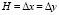 
; ?t = 9,263×10-7 с; E = 6,958×104 МПа (7,1×105 кгс/см2); ν = 0,34; ρ = 2,7×103 кг/м3 (2,755×10-6 кгс с2/см4); Cp = 5398 м/с; Cs = 3078 м/с. Приняты следующие допущения: 1 кгс/см2 ≈ 0,098 МПа; 1 кгс с2/см4 ≈ 0,98×109 кг/м3.
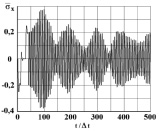
Рис. 7. Изменение упругого нормального напряжения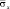 
во времени t/?t в точке B4 (соотношение ширины к высоте консоли – один к десяти)
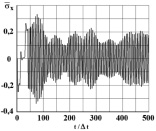
Рис. 8. Изменение упругого нормального напряжения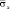 
во времени t/?t в точке B5 (соотношение ширины к высоте консоли – один к десяти)
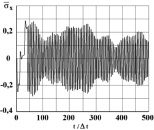
Рис. 9. Изменение упругого нормального напряжения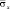 
во времени t/?t в точке B6 (соотношение ширины к высоте консоли – один к десяти)
В расчетах принимается минимальный шаг по времени, то есть ?t = 9,263×10-7.
Исследуемая расчетная область имеет 4008004 узловых точек. Решается система уравнений из 16032016 неизвестных.
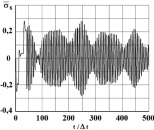
Рис. 10. Изменение упругого нормального напряжения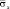 
во времени t/?t в точке B7 (соотношение ширины к высоте консоли – один к десяти)
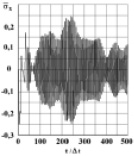
Рис. 11. Изменение упругого нормального напряжения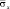 
во времени t/?t в точке B8 (соотношение ширины к высоте консоли – один к десяти)
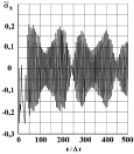
Рис. 12. Изменение упругого нормального напряжения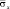 
во времени t/?t в точке B9 (соотношение ширины к высоте консоли – один к десяти)
На рис. 4–13 представлено изменение упругого нормального напряжения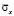 
(
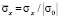) во времени n в точках B1–B10 консоли (рис. 3).
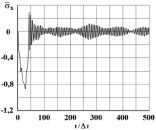
Рис. 13. Изменение упругого нормального напряжения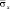 
во времени t/?t в точке B10 (соотношение ширины к высоте консоли – один к десяти)
Выводы
1. Для прогноза безопасности объекта, находящегося в воздушной и твердой деформируемой среде, при волновых воздействиях применяется численное моделирование.
2. Разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при волновых воздействиях.
3. Матрица упругости выражена через скорость продольных волн, скорость поперечных волн и плотность.
4. Исследуемая область разбивается по пространственным переменным на треугольные и прямоугольные конечные элементы первого порядка. По временной переменной исследуемая область разбивается на линейные конечные элементы первого порядка.
5. За основные неизвестные приняты два перемещения и две скорости перемещений в узле конечного элемента.
6. Линейная динамическая задача с начальными и граничными условиями в виде дифференциальных уравнений в частных производных приведена к системе линейных обыкновенных дифференциальных уравнений с начальными условиями, которая решается по явной двухслойной схеме.
7. Растягивающее упругое нормальное напряжение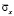 
от точки B1 до точки B10 консоли изменяется от значения 
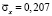до значения 
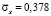. Сжимающее упругое нормальное напряжение 
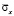от точки B1 до точки B10 консоли изменяется от значения 
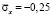до значения 
.
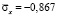8. Полученные результаты можно оценить как первое приближение к решению сложной комплексной задачи о воздействии воздушной ударной волны на консоль с упругой полуплоскостью, с помощью численного моделирования волновых уравнений теории упругости.