Постановка задачи при нестационарных сейсмических воздействиях
Волны напряжений различной природы, распространяясь, в деформируемом теле взаимодействуют, друг с другом, что приводит к образованию новых областей возмущений, перераспределению напряжений и деформаций.
При интерференции волн напряжений их интенсивности складываются. Они могут достигать значений, превосходящих предел прочности материала. В этом случае наступает разрушение материала.
После трехкратного или четырехкратного прохождения и отражения волн напряжений в теле процесс распространения возмущений становится установившимся, напряжения и деформации усредняются, тело находится в колебательном движении.
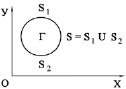
Рис. 1. Некоторое тело Г в прямоугольной декартовой системе координат XOY
Некоторые вопросы в области моделирования нестационарных динамических задач с помощью применяемого метода, алгоритма и комплекса программ рассмотрены в следующих работах [1–10].
Для решения задачи о моделировании упругих нестационарных волн напряжений в деформируемых областях сложной формы рассмотрим некоторое тело Г в прямоугольной декартовой системе координат XOY (рис. 1), которому в начальный момент времени t = 0 сообщается механическое нестационарное импульсное воздействие.
Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
,
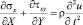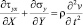(x, y)∈Г,
,
, 
,
, 
, 
,
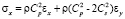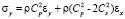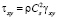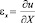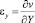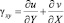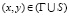, (1)
где σx, σy и τxy – компоненты тензора упругих напряжений; εx, εy и γxy – компоненты тензора упругих деформаций; u и v – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ – плотность материала;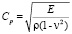 
– скорость продольной упругой волны; 
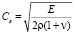– скорость поперечной упругой волны; ν – коэффициент Пуассона; E – модуль упругости; 
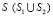– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
Разработка методики и алгоритма
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями (1) используем метод конечных элементов в перемещениях. Задача решается методом сквозного счета, без выделения разрывов. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
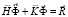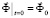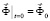, (2)
где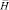 
– диагональная матрица инерции; 
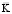– матрица жесткости; 
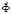– вектор узловых упругих перемещений; 
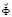– вектор узловых упругих скоростей перемещений; 
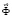– вектор узловых упругих ускорений; 
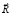– вектор внешних узловых упругих сил.
Соотношение (2) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями (1) привели к линейной задаче Коши (2).
Для интегрирования уравнения (2) конечноэлементным вариантом метода Галеркина приведем его к следующему виду
, 
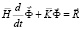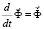. (3)
Интегрируя по временной координате соотношение (3) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
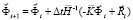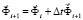. (4)
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина.
Общая теория численных уравнений математической физики требует для этого наложение определенных условий на отношение шагов по временной координате Δt и по пространственным координатам, а именно
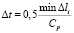
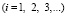, (5)
где Δl – длина стороны конечного элемента.
Для исследуемой области, состоящей из материалов с разными физическими свойствами, выбирается минимальный шаг по временной координате (5).
В работах [3–4, 6–8] приведена информация о физической достоверности и математической точности моделирования нестационарных волн напряжений в деформируемых телах с помощью рассматриваемого численного метода, алгоритма и комплекса программ.
Определение нестационарных волновых напряжений в Курпсайской плотине
В работах [1–3, 5, 10] приведена информация о моделировании нестационарных волн напряжений в деформируемых объектах при сейсмических воздействиях с помощью применяемого численного метода, алгоритма и комплекса программ.
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ ≈ 0,1 МПа; 1 кгс с2/см4 ≈ 109 кг/м3.
Рассматривается задача о воздействии плоской продольной упругой волны на Курпсайскую плотину с основанием (рис. 2).
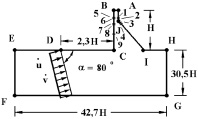
Рис. 2. Постановка задачи для системы сооружение-основание (Курпсайская плотина)
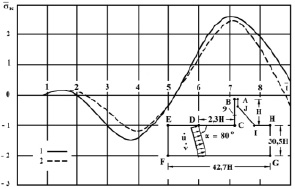
Рис. 3. Изменение упругого контурного напряжения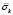 
в точке 9 во времени 
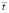на контуре Курпсайской плотины при воздействии плоской продольной упругой волны типа полупериода синусоиды при λ/H = 3
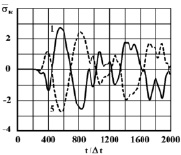
Рис. 4. Изменение упругого контурного напряжения 
в точках 1 и 5 на контуре Курпсайской плотины во времени t/Δt
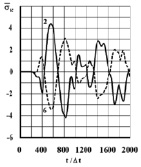
Рис. 5. Изменение упругого контурного напряжения 
в точках 2 и 6 на контуре Курпсайской плотины во времени t/Δt
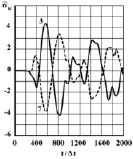
Рис. 6. Изменение упругого контурного напряжения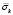 
в точках 3 и 7 на контуре Курпсайской плотины во времени t/Δt
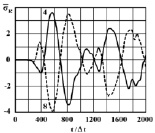
Рис. 7. Изменение упругого контурного напряжения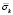 
в точке 4 и 8 на контуре Курпсайской плотины во времени t/Δt
Начальные условия приняты нулевыми. В сечении на расстоянии 2,3H (рис. 2) (H = 115 м) при 0 ≤ n ≤ 25 (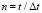
) скорости упругих перемещени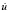й 
и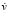 
изменяются линейно от 0 до 
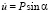и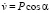 
, а при n > 25 
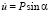и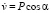 
(
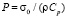,σ0 = 0,1 МПа (1 кгс/см2)).
Контур плотины HIJABCDE (кроме точки D) предполагается свободным от нагрузок при t > 0. Граничные условия для контура EFGH при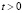 
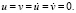Отраженные волны от контура EFGH не доходят до исследуемых точек при 0 ≤ n ≤ 2000. Расчеты проведены при следующих исходных данных: H = 115 м; Δt = 0,742·10-3 c; E = 0,36·104 MПа (0,36·105 кгс/см2); n = 0,36; r = 0,122·104 кг/м3 (0,122·10-5 кгс с2/см4); Cr = 1841 м/с.
Исследуемая расчетная область имеет 953 узловых точек. Курпсайская плотина аппроксимирована 224 узловыми точками.
На рис. 3 показано изменение контурного напряжения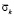 
в точке 9 во времени 
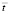, полученное с помощью интеграла Дюамеля при воздействии типа полупериода синусоиды при λ/H = 3 (λ – длина волны): 1 – результаты численного решения, полученные методом конечных элементов в перемещениях [3]; 2 – результаты численного решения, полученные смешанным методом конечных элементов [3]. Расхождение для максимального упругого контурного напряжения составляет 5 %.
На рис. 4–7 показано изменение контурных напряжений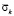 
в Курпсайской плотине во времени t/Δt.
Выводы
1. Курпсайская плотина моделируется с упругим основанием без заполненного водохранилища.
2. Упругое контурное напряжение на гранях Курпсайской плотины является почти зеркальным отражением одна другой, то есть антисимметричным.
3. Курпсайская плотина при сейсмическом воздействии работает как стержень переменного сечения, то есть если на одной грани растягивающие напряжения, то на другой сжимающие напряжения.
4. На контурах Курпсайской плотины при сейсмическом воздействии в основном преобладают изгибные волны.
5. Максимальное растягивающее напряжение возникает в верхней части задней области контура Курпсайской плотины.