Применение достижений фундаментальных наук, в том числе математики, в настоящее время наблюдается в самых различных областях: в экономике, лингвистике, в медицине. В настоящее время достигнуты большие успехи в понимании основных закономерностей в области биологии и медицины. Повысился интерес к выявлению общих принципов функционирования организмов, к пониманию сущности жизни. Все это и послужило предпосылками к проникновению в медицину математических методов. В медицинских исследованиях математика может быть использована с одной стороны для обработки результатов эксперимента, с другой – для создания различных математических моделей, описывающих те или иные процессы, происходящие при жизнедеятельности живого организма, а также для диагностирования различных заболеваний. Математический подход к решению задач диагностирования в медицине сводится не только к применению каких-либо математических приемов, расчетных формул и т.п., а прежде всего в выработке общих понятий, к созданию моделей, пригодных для изучения и выяснении фундаментальных принципов организации изучаемых систем.
Математический подход в медицинских исследованиях открывает новые возможности в решении диагностических задач. При диагностировании заболеваний происходит переработка информации в логической последовательности (диагностический алгоритм) с применением математических моделей диагностирования адекватные врачебной логике. Разработанные [1-3] информационно-математические модели диагностирования и прогнозирования на основе методов теории нечетких множеств показывают перспективность такого подхода.
Диагностические таблицы, используемые в здравоохранении и встречающиеся в научных публикациях, представляют собой формализованную базу данных по соответствующим заболеваниям в рамках одного нозологического класса. Диагностическими признаками могут быть как количественно-аналоговые (температура тела, артериальное давления, содержание СОЭ в крови и т.д.), так и бинарные (параметр в норме / не в норме, наличие / отсутствие раковых клеток в срезе и т.д.), а также нечетко выраженные (незначительное покраснение кожи, сильные боли в области сердца и т.д.). Степень соотношения признаков (симптомов) к соответствующим заболеваниям также могут быть представлены как в количественном виде, так и в виде качественного описания (характерно, редко, возможно и т.д.). Лингвистические переменные (признаки) требуют соответствующего представления в числовом эквиваленте.
Задача диагностирования различных заболеваний, основывающаяся на сложной и нечеткой информации, является актуальной. Биологические, в том числе и медицинские, информации носят в основном описательный характер, собранием более или менее систематизированных результатов наблюдений и экспериментов. Однако, обнаружены глубокие связи между явлениями, которые прежде представлялись обособленными.
Предлагается математическая модель диагностирования заболеваний на основе метода проекции градиентов. Заболевания относятся к одному нозологическому классу. Составленная матрица полезностей для этих заболевании (токсический зоб, вегетативная сосудистая дистония), основываются на статистических данных взятых из практического здравоохранения. Обозначим заболевания: A1-контрольная группа, А2-диффузный токсический зоб, А3-вегетативная сосудистая дистония. Причем (контрольная группа) соответствует возможному нормальному состоянию пациента, без соответствующей патологии, либо не относящихся к рассматриваемым заболеваниям. Допустим, у пациента наблюдается плохой сон, одышка, учащенное сердцебиение, боль в области сердца, потливость, потери в весе и состояние пациента задано множеством:
X~ = {0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.7/X9}.
Значения (0.4; 0.2; 0.5; 0.2; 0.6; 0.7;) означают степень выраженности симптомов для данного пациента, которую представим в виде вектора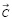 
:
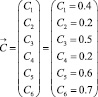
и полезности для данного нозологического класса, взятые из диагностической таблицы, в виде матрицы А:
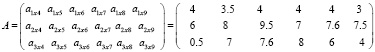
И находим: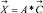 
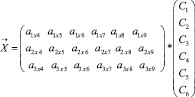
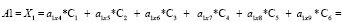
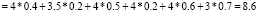
Аналогично: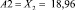 
и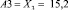 
Отсюда множество: μ(Aio)~Ao (μ(A1o)) = max (8.6; 18.96; 15.2;).
Поскольку: A(*) = μ ~ (A2o) = 18.96 то, оптимальной альтернативой является заболевание A2. Отсюда диагноз: наблюдается заболевание диффузный токсический зоб для заданного состояния системы и наблюдаемого у пациента симптомокомплекса.
С целью проверки полученного результата определим диагноз известным вероятностно-статистическим методом, в основе которого лежит формула Байеса.
,
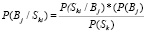где условные вероятности симптомокомплекса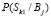 
вычисляются:
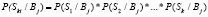
Полная вероятность наличия симптомокомплекса находится:
.
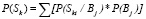P(Bj) – априорные вероятности, определяемые как характеристики распространения болезней в данной группе населения с учетом географических, сезонных эпидемиологических факторов, считаем одинаковыми (для простоты расчетов).
Полученны вероятности заболеваний (0.1, 0.78, 0.2) соответственно для контрольной группы, диффузного токсического зоба и вегетативной сосудистой дистонии. Результаты показывают, что для данного пациента, имеющего перечисленный выше симптомокомплекс, наиболее вероятно заболевание: диффузный токсический зоб. Как видно, диагнозы совпали, что свидетельствует о корректности полученных результатов. Разработанная нами математическая модель диагностирования заболеваний универсальна и имеет существенное преимущество, так как в нем учитывается не только степень принадлежности (полезности μ(Xk)) симптомов заболеваниям, но и состояние системы, описываемое нечетким множеством:
X~ =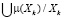 
где μ(Xk) – степень выраженности симптома, что позволяет считать предлагаемую модель более уникальной и возможности которой гораздо шире.
Медицине, при диагностировании различных заболеваний, приходится решать задачи, основываясь на сложной и часто нечеткой информации, каковыми являются, например, клинико-анамнестические данные, поступающие от человека, иногда единственного источника информации. Применение математических моделей диагностирования понижает субъективизм и повышает достоверность при принятии решений.
Современные образовательные системы включают в себя инновационные технологии использующие, в частности, различные диагностирующие модели. В этом плане разработанная математическая диагностирующая модель становится важным элементом в процессе обучения. С помощью данной системы можно производить мониторинг по различным заболеваниям, основываясь на имеющихся базы данных, что свидетельствует о перспективности исследования.