В настоящей работе рассмотрим вопросы численного моделирования уравнения переноса-дифузии на примере расчетов, выполненных для оценки загрязнения приземного слоя атмосферы промышленными выбросами.
Предлагаем на численнную реализацию модели переноса-диффузии примеси наложить следующие ограничения. Программная реализация модели предназначена для природоохранных служб заводов и должна работать на машинах класса РС АТ 486. Отсюда следует, что модель предназначается для моделирования приземного слоя атмосферы в окрестности (ограниченной радиусом 10-20 км) промышленных предприятий. А отсюда следует, что в расчетной модели течений скорости может быть либо вообще будут постоянны в расчетной области. Упрощающее предположение о постоянстве скорости в расчетной области может быть оправдано ее относительно небольшими пространственными масштабами и тем, что заводы стремятся строить на относительно ровных, хорошо «продуваемых» ветрами площадках. Химическую трансформацию примесей можно не учитывать и нестационарные процессы не рассматривать, сделать это не позволят уже упоминавшиеся вычислительные ресурсы.
Пусть источники выбросов находятся внутри цилиндра, нижняя грань которого – подстилающая поверхность (земля).
В своей основе все математические модели процесса распространения той или иной примеси опираются на полуэмпирическое дифференциальное уравнение переноса:
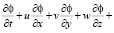
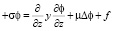(1)
Здесь Φ – искомая концентрация примеси; t – время; u, v, w – компоненты скорости ветра по осям x, y, z декартовой системы координат соответственно; μ – коэффициент турбулентной диффузии в плоскости (x,o,y); γ – коэффициент турбулентной диффузии в z-направлении (z-высота);
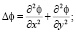
ƒ – источниковый член, зависящий в общем случае от координат и времени, то есть ƒ = ƒ (y, z, t);
σ – величина, связанная с трансформацией (поглощением) субстанции (в общем случае σ = σ (x, y, z, t)).
Обычно требуется еще условие соленоидальности поля скоростей, то есть компоненты скорости в каждой точке области в любой момент времени должны удовлетворять уравнению неразрывности:
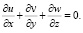
Наиболее распространенными граничными условиями для уравнения (1) являются следующие:
Φ = ΦP – на боковой поверхности цилиндра, представляющего расчетную область (условие означает, что граница удалена от источника настолько далеко, что концентрация выбрасываемого источником полютанта, загрязняющей атмосферу примеси, не вносит существенного вклада в фоновую концентрацию);
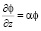– в нижнем основании цилиндра (z = 0) (условие «прилипания» примеси; трава, деревья, городская застройка удерживают примесь (дым, газ) в своих «порах» и они сами могут служить источником загрязнения атмосферы);
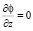– в верхнем основании цилиндра (z = H) (на верхней границе происходит поглощение, уничтожение полютанта или самоочищение атмосферы), где ΦP – фоновая концентрация примеси; α – коэффицент, учитывающий «прилипание» примеси к поверхности Земли.
В общем случае то или иное решение уравнения (1) (по сути – распределение концентраций примеси в любой момент времени) приходится находить путем численного интегррования последнего. Однако в ряде случаев, наложив определенные ограничения на процесс распространения примеси, можно получать те или иные аналитические (формульные) решения.
В случае, когда для описания процесса распространения примеси используется двумерное уравнение
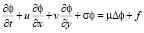(2)
то, несмотря на его внешнее сходство с (1), под концентрацией ν следует понимать интегральную по высоте концентрацию примеси. Ее размерность –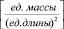 
, а не традиционная 
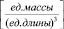, поэтому значение концентрации ν, полученное по двумерной методике, должно быть «размыто» по высоте слоя Н, внутри которого реально и происходит процесс распространения. Проще всего сделать, разделив ν на Н, тем самым предположив распределение равномерным.
Следует заметить, что уравнение (1) описывает процесс распространения субстанции ν в среде, свойства (u, ν, w, σ, γ, μ, ƒ) которой не зависят от данного процесса, то есть обратное влияние примеси на характеристики среды не учитывается. Это вполне соответствует физике упомянутого процесса, поскольку объемные (массовые) концентрации примеси в среднем незначительны. В случае распространения тяжелой примеси вместо z – компоненты скорости w в уравнении (1) должна стоять скорость (w-wg), где wg – скорость оседания частиц под действием силы тяжести.
Аналитическая модель. Рассмотрим стационарную задачу (3), когда скорости ветра u = const и ν = const. Тогда решение уравнения переноса для точечного источника ВСВ:
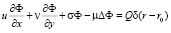(3)
будем искать в виде:
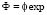
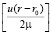(4)
где u(r-r0) = u(x-x0) + ν(y-y0), и подставляя (4) в уравнение (3) приходим к уравнению относительно Φ:
– μΔΦ + βΦ = QΔ(r-r0), (5)
где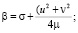 
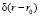– дельта-функция: 1, если r = r0 
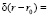{ 0, если r ≠ r0
Тогда решение уравнения (5) в плоскости (x, y) дается формулой
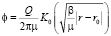, (6)
где K0 – функция Макдональда, имеющая вид:
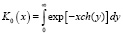, х > 0. (7)
С учетом (6) получаем решение уравнения (3) [1]:
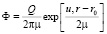
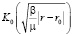(8)
Оценим характерные размеры области Q, при которых формула (8) дает приблеженное решение задачи, где на границе области E концентрация примесей должна быть нулевой. Введем малую величину Е такую, что при Ф ≤ Е выполняется краевое условие на границе области. Выбор Е обусловливается фоновой концентрацией, а также тем минимальным уровнем, при котором влиянием данного типа примесей можно пренебречь [1].
Полагая априори величины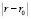 
такими, что справедлива асимптотическая формула
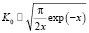(9)
и используя неравенство (ur-r0)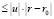
, находим
,
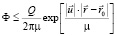
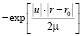
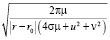откуда приходим к соотношению:
,
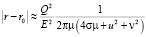выполнение которого при выборе области определения решения G, гарантирует решение краевой задачи с заданной степенью точности Е.
Основные трудности, связанные с получением аналитического решения для задачи (3), обусловлены вычислением функции Макдональда (7). Вычисление интеграла (7) на полубесконечной области представляет собой трудную задачу. Поэтому будем аппроксимировать функцию Макдональда полиномом, степень которого возьмем из условия точности аппроксимации. Для точности аппроксимации порядка 10–6 выбрали полином 12 степени. Такая высокая точность аппроксимации необходима для тестирования численных решений. Для описания реальных ситуаций такая точность не требуется, поскольку данная модель для этого малопригодна.
При малых значениях аргумента х использовалось асимптотическое представление. Тогда решение задачи (3) можно представить в следующем виде:
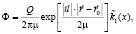при x < 2 (10)
где
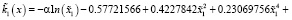
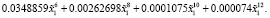
Здесь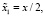 
где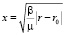 
;
,
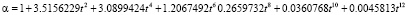где t = x/3.75
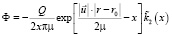, при x ≥ 2. (11)
Здесь
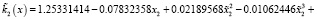
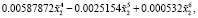
где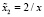 
.
Точность выполнения разложения функции Макдональда проверялась на таблицах специальных функций [2] – совпадение до шестого знака после десятичной запятой. Решения (10, 11) использовались при тестировании численного метода решения двумерной задачи переноса (3), получено совпадение до шестого знака. Из проведенных сравнений следует, что решение задачи переноса (10, 11) для точечного источника единичной интенсивности (Q = 1) с точностью до 10-6 описывает процессы переноса полютантов в атмосфере в рамках данной модели.
Основные недостатки аналитической модели связаны с постоянством коэффицентов переноса (σ, μ) и скоростью ветра. При этом фоновая концентрация выброса должна быть нулевой. В противном случае необходимо задавать дополнительный эффективный источник, который мог бы обеспечить существующую фоновую концентрацию полютантов.
Основные преимущества аналитической модели заключаются в ее простой численной реализации, в быстроте счета. С помощью аналитического решения можно получить фрагментарное распределение загрязняющих веществ в любой заданной области, не решая краевой задачи.
Область расчетов покроем сеткой таким образом, чтобы источники выбросов попадали в узлы сетки. Для аналитической модели это не существенно, но мы будем использовать и в численных методах туже сетку, там это требование просто необходимо. На практике в сеточный узел помещают эффективный источник, в котором учтены все источники, находящиеся в окрестности узла. Тогда каждый узел можно рассматривать как отдельный точечный источник с заданной интенсивностью и, используя решение (10, 11), можно получить распределение загрязняющих веществ от каждого источника независимо от других. Решение в произвольной точке расчетной области будет суммой вкладов в загрязнение от всех точечных источников. Пусть xi, yi – координаты расчетной области, в которой необходимо получить решение задачи, а xL, yM – координаты источников. Тогда
,
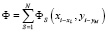где N – число точечных источников, а функция
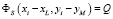
при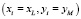 
.
Из приведенных расчетов видно, что аналитическая модель хорошо описывает процесс распространения выбросов в атмосфере при постоянных коэффицентах переноса и может быть использована в качестве теста для проверки численных расчетов и для оперативного получения предварительной информации о распространении примеси.