При динамическом и импульсном воздействии в сооружении распространяются волны напряжений. Волны напряжений образуют области возмущений. Материал находится в напряженно-деформированном состоянии. При волновом воздействии существуют локализованные напряжения и деформации, способствующие возникновению разрушения в одной части тела независимо оттого, что происходит в другой его части.
Напряженное состояние импульсного (волнового) нагруженного тела может изменяться так быстро, что возникающие деформации и разрушения еще не успевают распространиться, как распределение напряжений изменится, так как скорости распространения волн напряжений достигают 6000 м/с, а нарушение прочности (трещины) распространяются со скоростью не более 1500 м/с.
Многие разрушения, которые вызваны волновыми нагрузками, можно объяснить, рассматривая влияние, которое оказывает геометрическая форма тела на волны напряжений. Отражение от свободных поверхностей волн сжатия приводит к появлению растягивающих волн, которые, распространяясь по телу, интерферируют друг с другом.
В результате взаимодействия волн напряжений наблюдаются некоторые явления: разрушение, имеющее место при интерференции прямой и отраженной волн, называемой отколом; угловые разрушения, возникающие в угловых точках при взаимодействии двух или нескольких волн, которые отражаются от свободных поверхностей.
При отражении прямой волны сжатия от свободной поверхности тела зарождается отраженная волна растяжения. Интерференция прямой и отраженной волн может вызвать растягивающее напряжение. Это явление обычно развивается на небольшом расстоянии от свободной поверхности. Величина растягивающего напряжения достаточна для разрушения материала. При разрушении происходит откол.
Для решения двумерной нестационарной динамической задачи математической теории упругости с начальными и граничными условиями используем метод конечных элементов в перемещениях.
Практическая реализация математического моделирования волн напряжений в сложных деформируемых телах с помощью разработанного численного метода, алгоритма и комплекса программ приведена в следующих работах [1–10].
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
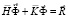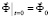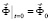, (1)
где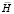 
– диагональная матрица инерции; 
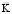– матрица жесткости; 
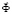– вектор узловых упругих перемещений; 
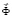– вектор узловых упругих скоростей перемещений; 
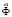– вектор узловых упругих ускорений; 
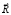– вектор внешних узловых упругих сил.
Интегрируя уравнения (1) конечноэлементным вариантом метода Галеркина, получим явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
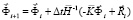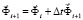. (2)
Шаг по временной переменной координате ?t выбирается из следующего соотношения
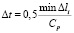
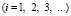, (3)
где ?l – длина стороны конечного элемента.
В работах [1–4, 6–9] приведена информация о верификации численного моделирования нестационарных волн напряжений в областях различной формы с помощью разработанного метода, алгоритма и комплекса программ.
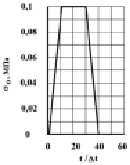
Рис. 2. Ударное воздействие в виде трапеции для задачи без полости
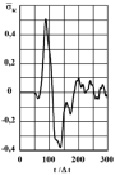
Рис. 3. Изменение упругого контурного напряжения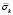 
во времени t/?t в точке A1
На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при ударных воздействиях на сооружения.
Рассмотрим задачу о воздействии упругой ударной волны (рис. 2) на фундамент машин без полости (рис. 1).
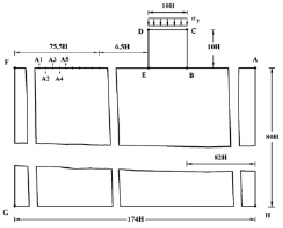
Рис. 1. Постановка задачи о воздействии упругой ударной волны на фундамент машин
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ ≈ 0,1 МПа; 1 кгс с2/см4 ≈ 109 кг/м3.
На контуре CD приложено нормальное воздействие σу (рис. 1), которое при 0 ≤ n ≤ 10 (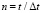
) изменяется линейно от 0 до P, при 11 ≤ n ≤ 30 равно P и при 31 ≤ n ≤ 40 от P до 0 (P = σ0, σ0 = – 0,1 МПа (-1 кгс/см2)). Граничные условия для контура FGHA при t > 0 
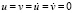. Отраженные волны от контура FGHA не доходят до исследуемых точек при 0 ≤ n ≤ 200. Контуры DEF и CBA свободны от нагрузок, кроме точек D и C, где приложено воздействие.
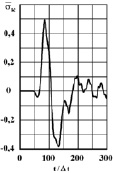
Рис. 4. Изменение упругого контурного напряжения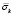 
во времени t/?t в точке A2
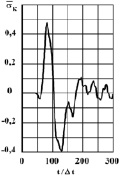
Рис. 5. Изменение упругого контурного напряжения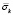 
во времени t/?t в точке A3
Расчеты проведены при следующих исходных данных: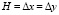 
; ?t = 1,393× ×10-6 с; E = 3,15×104 МПа (3,15×105 кгс/см2); ν = 0,2; ρ = 0,255×104 кг/м3 (0,255×10-5 кгс с2/см4); Cp = 3587 м/с; Cs = 2269 м/с.
Исследуемая расчетная область имеет 14320 узловых точек. Решается система уравнений из 57280 неизвестных.
На рис. 3–7 показано изменение упругого контурного напряжения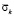 
(
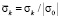) во времени n в точках A1–A5 (рис. 1), находящихся на свободной поверхности упругой полуплоскости (расстояние между точками: A1 и A2 равно H; A2 и A3 равно H; A3 и A4 равно H; A4 и A5 равно H).
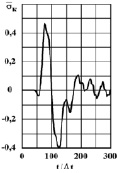
Рис. 6. Изменение упругого контурного напряжения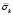 
во времени t/?t в точке A4
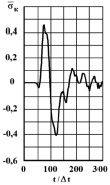
Рис. 7. Изменение упругого контурного напряжения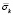 
во времени t/?t в точке A5
Выводы
1. Для прогноза безопасности фундамента машин при воздействии упругой ударной волны применяется численное моделирование. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при ударных воздействиях на сооружения.
2. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Матрица упругости выражена через скорость продольных волн, скорость поперечных волн и плотность.
3. Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений. За основные неизвестные приняты два перемещения и две скорости перемещений в узле конечного элемента.
4. Задачи решаются методом сквозного счета, без выделения разрывов. Применяется кусочно-линейная аппроксимация для уменьшения влияния разрывов на точность результатов численного решения, полученных с помощью метода конечных элементов в перемещениях.
5. Линейная динамическая задача с начальными и граничными условиями в виде дифференциальных уравнений в частных производных, для решения задач при ударных воздействиях, с помощью метода конечных элементов в перемещениях приведена к системе линейных обыкновенных дифференциальных уравнений с начальными условиями, которая решается по явной двухслойной схеме.
6. Решена задача о воздействии упругой ударной волны на фундамент машин. Исследуемая расчетная область имеет 14320 узловых точек. Решается система уравнений из 57280 неизвестных. Получены напряжения в точках на поверхности упругой полуплоскости около фундамента машин. Растягивающее упругое контурное напряжение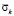 
имеет следующее максимальное значение 
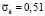. Сжимающее упругое контурное напряжение 
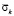имеет следующее максимальное значение 
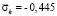. Растягивающее упругое нормальное напряжение 
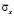имеет следующее максимальное значение 
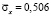. Сжимающее упругое нормальное напряжение 
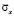имеет следующее максимальное значение 
.
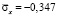7. Полученные результаты можно оценить как первое приближение к решению сложной комплексной задачи о безопасности фундамента с основанием при нестационарных ударных воздействиях.