Известен феномен холодных ядерных трансмутаций, в результате которых выделяется больше тепловой энергии, чем затрачивается на их реализацию [1, 2]. Для ядерных реакций с водородом (или дейтерием) необходимо доставить протоны к ядрам элементов, преодолев кулоновский барьер отталкивания. Это можно сделать, если располагать атомами водорода в необычных субатомных состояниях, таких, которые образуют компактные в пространстве нейтральные состояния с энергией связи значительно превосходящей энергию связи атома водорода. В этом случае вероятность ядерных реакций существенно возрастает, поскольку субатомы водорода могут приближаться к ядрам элементов, в том числе сближаться между собой, значительно ближе, чем собственно протоны при тех же энергиях.
Нам идеологически наиболее близок подход, развиваемый Ю.Л. Ратисом в работе [1], в которой показана возможность перехода начального состояния системы «электрон плюс протон» в метастабильный «нейтроний» с максимально возможной энергией связи ~ 103 эВ. Размеры нейтрония относительно велики и сопоставимы с размерами атома водорода.
Возможность существования субатомных состояний атома водорода покажем с помощью использования формулы де Бройля:
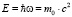 (1)
(1)
Смысл этой формулы заключается в том, что элементарная частица с массой покоя m0 имеет собственную квантовую энергию движения с частотой ω, несвязанную с поступательным движением квантовой частицы. Эта формула предложена де Бройлем в 1923 году в своей докторской диссертации. Она ценна следствиями, которые из неё вытекают [3].
Субатомные состояния атома водорода возможны тогда, когда расстояния между протоном и электроном настолько малы, что перекрываются области их пространственной локализации, вызванные наличием собственной квантовой энергии движения.
Постановка задачи
Уравнение для отыскания энергии связи системы, состоящей из электрона (индекс 1) и протона (индекс 2) запишется в виде:
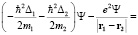
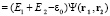 (2)
(2)
Здесь 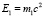 ,
, 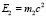 – собственные энергии электрона и протона, ε0 – энергия связи субатома. Система координат расположена в центре распределения вероятности системы из двух частиц.
– собственные энергии электрона и протона, ε0 – энергия связи субатома. Система координат расположена в центре распределения вероятности системы из двух частиц.
В уравнении (2) попробуем «выключить» вклад движения протона в полную энергию системы и свести задачу к одноэлектронному виду. Учтем, что масса протона существенно превосходит массу электрона m2 >> m1 и комптоновская длина электрона r10 много больше комптоновской длины протона r20, r10 >> r20, где 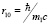 и
и 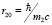 . Это неравенство позволяет поместить начало координат в центре локализации протона, поскольку собственная пространственная область локализации протона значительно меньше области собственной локализации электрона. Тогда из (2) имеем:
. Это неравенство позволяет поместить начало координат в центре локализации протона, поскольку собственная пространственная область локализации протона значительно меньше области собственной локализации электрона. Тогда из (2) имеем:
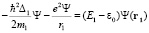 (4)
(4)
Внешне уравнение (4) напоминает задачу о традиционном атоме водорода. Это одночастичное приближение для двухчастичной квантовой системы в нашем случае несколько ущербно и главное не учитывает наличия спина у протона и не может предсказать орто- и парасостояний субатомного водорода. В работе [4] сделана попытка решить это уравнение методом теории возмущений для случая E1 >> ε0. Такой подход вдохновлялся оценками энергии связи «нейтрония» (порядка 103 эВ) и экспериментальными данными, приведенными в работе [1]. При E1 >> ε0 решение уравнения (4) не может дать обычного квантования энергии связи ε0. Использование в первом прядке теории возмущения является достаточно грубым приближением. Волновые функции нулевого приближения представляют собой неоднородные стоячие волны, интегралы от которых расходятся [4]. В связи с этим проводилось обрезание интегралов для получения наибольшей величины энергии связи.
Заметим, что в работе [5] автор проводит аналитический расчет системы «электрон + протон» со скачкообразным потенциалом, состоящим из кулоновской энергии и положительной модельной постоянной потенциальной энергии. Наличие постоянной составляющей энергии в принципе соответствует нашей задаче. Однако в нашем случае положительная энергия строго определена и равна собственной энергии электрона m1c2, кроме того учитываются спиновые состояния электрона.
Вычисление энергии связи для основного состояния
Для решения уравнения (4) используем сферическую систему координат и как обычно метод разделения переменных в задаче о падающей частице на силовой центр [6]. Представим 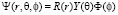 , получим уравнения:
, получим уравнения:
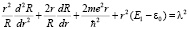 (5)
(5)
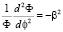 (6)
(6)
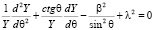 (7)
(7)
Сначала решаем уравнение (6). Его решение запишем в виде отличном от [6]:
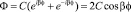 (8)
(8)
Здесь учитывается тот факт, что оба вращательных направления равновероятны, в результате имеем колебательные состояния по углу ?, а условие однозначности будет выполняться для составляющей плотности вероятности
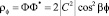 (9)
(9)
В результате имеем более общий ряд квантования: 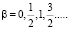 Далее примем
Далее примем 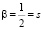 – величина, равная спину электрона, которая не должна изменяться во внешних полях, в том числе в поле протона.
– величина, равная спину электрона, которая не должна изменяться во внешних полях, в том числе в поле протона.
Найдем частное решение уравнения (7) для основного состояния в виде 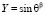 . Для констант разделения получим выражение
. Для констант разделения получим выражение 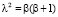 .
.
Для решения уравнения (5) введем безразмерную переменную 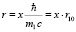
Получим:
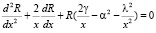 (10)
(10)
где 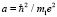 – боровский радиус атом водорода,
– боровский радиус атом водорода, 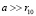 ,
, 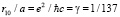 – постоянная тонкой структуры,
– постоянная тонкой структуры, 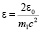 ,
, 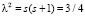 ,
, 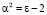 . Для свободной частицы ε = 0 и задача сводится к отысканию собственного волнового поля электрона. Такое поле вычислено аналитически в [4] и оно представляет собой радиальную стоячую неоднородную волну. Будем решать уравнение (10) в случае, когда ε > 2, полагая, что энергия связи должна превышать собственную энергию квантового движения электрона, чтобы удержать его в кулоновском поле протона. Это модель электронного облака, обусловленного собственной энергией движения электрона, в центре которого находится протон.
. Для свободной частицы ε = 0 и задача сводится к отысканию собственного волнового поля электрона. Такое поле вычислено аналитически в [4] и оно представляет собой радиальную стоячую неоднородную волну. Будем решать уравнение (10) в случае, когда ε > 2, полагая, что энергия связи должна превышать собственную энергию квантового движения электрона, чтобы удержать его в кулоновском поле протона. Это модель электронного облака, обусловленного собственной энергией движения электрона, в центре которого находится протон.
Решение будем искать в виде:
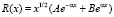 (11)
(11)
где 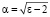 . В скобках опустим второе слагаемое, которое возрастает с увеличением координаты, и подставим искомое решение в уравнение (10). Получим:
. В скобках опустим второе слагаемое, которое возрастает с увеличением координаты, и подставим искомое решение в уравнение (10). Получим:
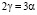 или
или 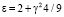
Тогда энергия связи равна практически собственной энергии квантового движения электрона
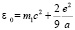 (12)
(12)
где а – боровский радиус. Среднее расстояние электрона от протона определим как:
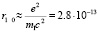 cм,
cм,
что более чем на пять порядков меньше, чем для традиционного атома водорода.
Таким образом, подтверждается исходная модель субатома водорода в виде облака электрона, обусловленная его собственной энергией движения, внутри которого находится протон. Энергия связи составляет ε0 ≈ 5?105 эВ, что на два порядка больше, предсказываемой ранее в [4]. При образовании таких атомов путем столкновения электрона с протоном, электрон нужно затормозить в области локализации протона с характерными размерами менее 2,8?10–13 см. Далее электрон может перейти в субатомное состояние с последующим излучением жесткого квант с энергией ε0. Необходимо также наличие магнитного поля для ориентации спинов заряженных частиц для образования орто- и парасостояний субатомов водорода. Полезно использовать магнитное поле и для торможения электронов относительно протонов до энергий равных энергии связи субатомов водорода. В целом различные способы производства субатомов водорода заслуживают патентования.
Экспериментальное доказательство существования субатомов водорода послужит подтверждением справедливости соотношения де Бройля (1).

