Одной из задач математического моделирования является разработка методов нахождения аналитических решений. Однако получение точных решений задач нелинейной теории упругости является одной из сложнейших проблем. В силу этого разрабатываются различные приближенные модели, позволяющие свести решение нелинейной задачи к решению ряда линейных задач. Одним из таких методов является метод конечных элементов, но в силу ограниченности ресурсов компьютеров, число конечных элементов в зонах больших градиентов рассчитываемых полей увеличивать невозможно. Поэтому данный подход плохо приспособлен к исследованию концентрации напряжений в зонах с большими градиентами напряжений, например, в окрестностях угловых точек отверстий. В связи с этим возникает задача разработки такого метода, который позволит свести решение нелинейных задач теории упругости к решению линейных задач и получить их аналитические решения. Данный аспект является важным, поскольку аналитические решения делают возможным анализ и оптимизацию влияния силовых и геометрических параметров на поведение решения, а численные методы нуждаются в аналитических решениях для проверки на пригодность.
Задача построения приближенной математической модели может быть осуществлена методом возмущений, предложенным в [5], который использует разложение в степенные ряды объектов, описывающих напряженно-деформированное состояние. Если удерживать один или два члена данного разложения, то будем получать решение в рамках эффектов первого или второго порядка. Для нахождения каждого члена разложения получается задача линейной теории упругости однородных тел, но с добавочными «внешними» поверхностными и объемными усилиями, зависящими от решений в рамках эффектов предыдущих порядков. Однако получаемые выражения достаточно громоздки, поэтому разложения выше второго порядка (эффектов второго порядка) редко используются. Появление современных пакетов символьной математики позволяет написать библиотеки программ, облегчающие действия с громоздкими выражениями, описывающими эффекты первого, второго или третьего порядков при произвольном напряженно-деформированном состоянии.
Применение пакета символьных вычислений Maple к решению задач нелинейной теории упругости
В работе [2] построена приближенная нелинейная модель плоской деформации несжимаемого однородного изотропного материала в рамках разложения по степеням малого параметра до третьего порядка включительно, позволяющая находить выражение коэффициента концентрации напряжений для различных форм отверстия при различных видах деформации.
Для нахождения аналитического решения задач нелинейной теории упругости в пакете символьной математики Maple создан комплекс программ, позволяющий проводить символьные вычисления в автоматическом режиме [1]. Все выполняемые операции распространены на тензоры, компоненты которых являются рядами по малому параметру до второго порядка включительно. Над этими тензорами, имеющими тип Array, получены процедуры для инвариантных дифференциальных операторов и процедуры выделения коэффициентов в этих разложениях по малому параметру, которые являются тензорами нулевого или первого ранга.
Все алгебраические операции над рядами в предположении их абсолютной сходимости выполняются в Maple пакетом powseries. Этим рядам достаточно придать вид разложения по малому параметру и зафиксировать порядок представления результата относительно данного параметра. Так моделируются эффекты соответствующего порядка. Для работы с дифференциальными уравнениями в частных производных используется пакет PDEtools. Граничные задачи линейной теории упругости для эффектов первого и второго порядков сводятся к интегральным уравнениям теории функций комплексной переменной [3]. В тех случаях, когда область отверстия имеет произвольную форму, необходимо рассмотреть комплексное представление перемещений и напряжений для эффектов первого и второго порядка. Для этого необходимо ввести в рассмотрение функцию z = υ(ξ), которая осуществляет конформное отображение внешности замкнутого контура на внешность окружности единичного радиуса 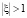 . Потребуем, чтобы точке ξ = ∞ соответствовала точка z = ∞. В качестве областей, характеризующих форму отверстия, рассматриваются только те, которые можно конформно отобразить на внешность окружности единичного радиуса с центром в начале координат с помощью функции вида
. Потребуем, чтобы точке ξ = ∞ соответствовала точка z = ∞. В качестве областей, характеризующих форму отверстия, рассматриваются только те, которые можно конформно отобразить на внешность окружности единичного радиуса с центром в начале координат с помощью функции вида
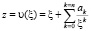 ,
,
где 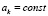
Для каждой из этих областей интегральные уравнения теории функций комплексного переменного приводятся к алгебраическим уравнениям с помощью интегралов типа Коши. Для эффектов первого и второго порядков искомые потенциалы аппроксимируются разложением в ряды Лорана, а коэффициенты находятся из условия удовлетворения граничным условиям на бесконечности и на контуре отверстия. При этом часть неизвестных коэффициентов находится из решения алгебраической системы линейных уравнений, полученной с помощью предельного перехода на бесконечности. Для нахождения остальных коэффициентов необходимо вычислить интегралы типа Коши на контуре отверстия.
Однако в пакете Maple нет специальных процедур и функций для точного вычисления интеграла типа Коши. Тем не менее, пользуясь основными свойствами интеграла типа Коши [3], можно реализовать алгоритм его точного вычисления.
Для эффектов второго порядка в интегральных уравнениях присутствует слагаемое вида
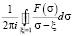 ,
,
которое зависит от решения, найденного в рамках эффектов первого порядка. Подынтегральная плотность F(σ) в зависимости от типа отверстия и граничных условий может быть достаточно сложной. В пакете Maple присутствуют возможности разложения функции в ряд в окрестности особой точки и асимптотических разложений в окрестности бесконечно удаленной точки. Этого достаточно для вычисления интегралов типа Коши на окружности единичного радиуса. Подынтегральная плотность является дробно-рациональной функцией и имеет особенности типа полюсов в бесконечно удаленной точке и в конечном наборе конечных точек 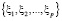 вне окружности единичного радиуса, являющихся корнями знаменателя. Средствами пакета Maple можно получить главные части разложений в ряды функции подынтегральной плотности F(ξ) в окрестностях этих точек в виде:
вне окружности единичного радиуса, являющихся корнями знаменателя. Средствами пакета Maple можно получить главные части разложений в ряды функции подынтегральной плотности F(ξ) в окрестностях этих точек в виде:
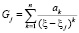 ,
,
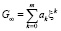 , j = 1, 2, …, p.
, j = 1, 2, …, p.
Тогда по [3] получаем
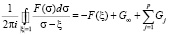
при интегрировании против хода часовой стрелки.
Ключевым моментом, от которого зависит успех вычисления интеграла типа Коши, является возможность точного нахождения корней знаменателя. В тех случаях, когда аналитически найти точное значение корней знаменателя поверхностной плотности F(σ) система Maple не может, приходится проводить вычисления интеграла типа Коши приближенными методами. В созданной библиотеке программ на базе пакета символьной математики Maple для приближенного вычисления интеграла типа Коши применяется следующая квадратурная формула [4]:
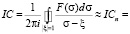
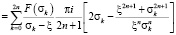 .
.
Здесь 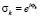 ,
, 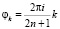 . Если
. Если 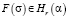 , то
, то 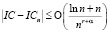 .
.
Задача о концентрации напряжений около отверстия полукруглой формы при равномерной нагрузке на бесконечности интенсивности p, Н/м2 в Maple
Рассмотрим задачу о концентрации напряжений около отверстия полукруглой формы при равномерной нагрузке на бесконечности. Без потери общности будем считать радиус отверстия равным единице. Контур отверстия свободен от напряжений. На бесконечности приложена равномерная радиальная нагрузка интенсивности p, Н/м2. Универсальным силовым параметром, имеющим ту же размерность, является модуль сдвига линейной теории упругости μ. Поэтому естественно возникает безразмерный малый параметр вида 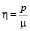 . Тогда на бесконечности вектор внешних сил
. Тогда на бесконечности вектор внешних сил 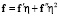 на площадках с нормальным вектором i имеет разложение
на площадках с нормальным вектором i имеет разложение 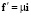 ,
, 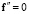 , а на площадке с нормальным вектором j разложение –
, а на площадке с нормальным вектором j разложение – 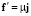 ,
, 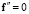 .
.
В цилиндрической системе координат {r, φ, z} введем единичный базис 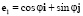 ,
, 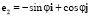 ,
, 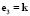 . Коэффициент концентрации напряжений в нелинейной теории, как и в классическом решении линейной теории, будем определять как
. Коэффициент концентрации напряжений в нелинейной теории, как и в классическом решении линейной теории, будем определять как 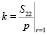 , где S22 – тангенциальная компонента «плоской» части тензора истинных напряжений Коши
, где S22 – тангенциальная компонента «плоской» части тензора истинных напряжений Коши 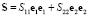 . Представление этой компоненты в рамках приближенной теории имеет вид
. Представление этой компоненты в рамках приближенной теории имеет вид 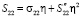 , откуда, вспоминая, что p = μη, получим выражение для коэффициента концентрации в рамках приближенной теории:
, откуда, вспоминая, что p = μη, получим выражение для коэффициента концентрации в рамках приближенной теории:
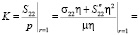
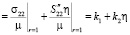 .
.
Конформное отображение внешности полукруга на внешность круга 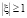 задается формулой
задается формулой
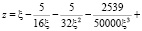
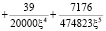 .
.
Вершинам заданного контура соответствуют значения полярного угла 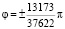 . Параметрические уравнения контура отверстия имеют вид:
. Параметрические уравнения контура отверстия имеют вид:
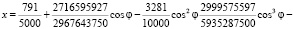
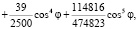
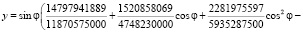
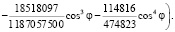
Для квадратичного приближения разложение коэффициента концентрации напряжений по малому параметру 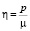 в вершинах полукруглого отверстия, соответствующих значениям
в вершинах полукруглого отверстия, соответствующих значениям 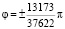 , принимает вид
, принимает вид 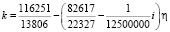 .
.
Таким образом, с увеличением величины интенсивности приложенной внешней нагрузки р наблюдаем изменение значения тангенциальных напряжений. Графики распределения относительных тангенциальных напряжений на внутреннем контуре отверстия, свободном от нагрузок, вычисленных в рамках эффектов первого и второго порядков при различных значениях параметра η, изображены на рис. 1 и рис. 2.
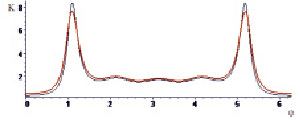
Рис. 1. Распределение относительных тангенциальных напряжений на контуре отверстия (развертка) при η = 0,2. Тонкая линия соответствует решению в рамках линейной теории, толстая линия соответствует квадратичному решению
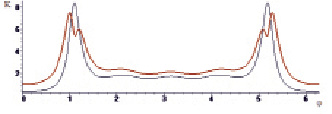
Рис. 2. Распределение относительных тангенциальных напряжений на контуре отверстия (развертка) при η = 0,8. Тонкая линия соответствует решению в рамках линейной теории, толстая линия соответствует квадратичному решению
Как видно из графиков, в квадратичном приближении при различных значениях параметра η максимум величины коэффициента концентрации напряжений K достигается при различных значениях φ, при этом его величина, по сравнению с классическим решением линейной теории, уменьшается. Заметим, что при учете внешней нагрузки p в разложении коэффициента концентрации напряжений наблюдаем эффект раздвоения одного максимума в вершине угловой точки на два несимметричных максимума в окрестности данной вершины. При этом в самой вершине достигается минимум.
Исследовав функцию 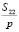 на экстремум, получаем, что значениям
на экстремум, получаем, что значениям 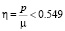 соответствует один экстремум: максимум достигается в вершинах полукруглого контура. При
соответствует один экстремум: максимум достигается в вершинах полукруглого контура. При 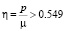 каждому значению малого параметра η соответствует три точки экстремума: в вершинах полукруглого отверстия достигается минимум, а двум другим корням производной
каждому значению малого параметра η соответствует три точки экстремума: в вершинах полукруглого отверстия достигается минимум, а двум другим корням производной 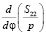 соответствуют максимумы.
соответствуют максимумы.
Максимальные значения коэффициента концентрации напряжений Kmax, вычисленные с точностью 10–6, и соответствующие им значения полярного угла φmax в зависимости от величины малого параметра η записаны в таблицу.
Экстремальные значения коэффициента концентрации Kmax и соответствующие им значения полярного угла φmax
|
|
K1max |
φ1max |
K2max |
φ2max |
|
0.1 |
8.0502930 |
1.100000000 |
– |
– |
|
0.2 |
7.6908140 |
1.092480468 |
– |
– |
|
0.3 |
7.3548587 |
1.079589844 |
– |
– |
|
0.4 |
7.1288716 |
1.053808594 |
– |
– |
|
0.5 |
7.0823218 |
1.033203125 |
– |
– |
|
0.549 |
7.1101293 |
1.025634766 |
6.2813205 |
1.141077637 |
|
0.6 |
7.1644955 |
1.018945312 |
6.1717449 |
1.164648438 |
|
0.7 |
7.3264786 |
1.008691406 |
6.0562580 |
1.184863281 |
|
0.8 |
7.5396336 |
1.000000000 |
6.0163771 |
1.198486328 |
|
0.9 |
7.7879480 |
0.994433594 |
6.0239863 |
1.209106446 |
Выводы
Метод эффектов второго порядка позволяет находить аналитическое решение плоских задач нелинейной теории упругости о концентрации напряжений на контуре отверстий. Данный алгоритм хорошо приспособлен для реализации в пакете символьной математики Maple.
На примере полости полукруглой формы исследовано влияние внешней нагрузки на величину коэффициента концентрации напряжений на контуре отверстия. Показано, что учет нелинейности в области концентраторов напряжений не только снижает значение тангенциальных напряжений, но и позволяет говорить об эффекте раздвоения одного максимума в вершине угловой точки на два симметричных максимума в окрестности данной вершины.