Дифференциальное уравнение отдачи тепла в окружающую среду имеет вид:
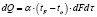(1)
С другой стороны, количество тепла внутри охлаждаемого тела, проходящее через ту же поверхность в единицу времени, также пропорционально ее площади, градиенту температуры по нормали к этой площади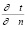 
и коэффициенту теплопроводности λ данного материала.
Дифференциальное уравнение имеет вид:
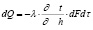(2)
Приравнивая правые части этих двух дифференциальных уравнений, получим выражение для определения коэффициента теплоотдачи:
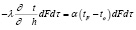(3)
Коэффициент теплопроводности λ, как правило, известен для ДМ, температуры нагрева поверхности tF и окружающей среды t0 определяются экспериментально. Для определения градиента температуры необходимо построить график зависимости изменения температуры по толщине подшипника скольжения, которая определяется экспериментально тонкими термопарами, расположенными по нормали к поверхности трения. По построенной графической зависимости определяют тангенс угла наклона касательной и соответствующие масштабы температур и длин.
,
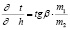где m1 и m2 – масштабы температур и длин.
Формула по определению коэффициента теплоотдачи экспериментальным путем:
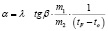(4)
Предлагаемый расчетно-экспериментальный метод определения коэффициента теплоотдачи α в подшипниках скольжения из ДМ является весьма простым, точным и позволяет определить α на любом участке охлаждаемой поверхности подшипника.