Нагруженным уравнением в частных производных второго порядка посвящены работы [1-10]. Общее определение этого широкого класса уравнений в частных производных было впервые дано А.М. Нахушевым в работах [7-8].
Многими авторами исследовались нелокальные краевые задачи для смешанных эллиптико – гиперболических и гиперболо – параболических уравнений второго порядка. Нелокальные краевые задачи для смешанного и смешанного нагруженного гиперболо – параболического типов уравнений более высокого порядка, то они остаются мало исследованными.
Цель работы состоит в постановке и исследовании однозначной разрешимости одной нелокальной краевой задачи для смешанного нагруженного уравнения третьего порядка.
Постановка задачи. Пусть Ω – конечная односвязная область, ограниченная отрезками AA0, А0B0, BB0 прямых x = 0, y = h, x = l соответственно, расположенных в полуплоскости y > 0, и характеристиками
AC:x + y = 0, BC:x – y = l
уравнения
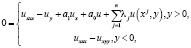(1)
Ω1 – параболическая, а Ω2 – гиперболическая части области Ω.
Предполагается, что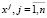 
– фиксированные точки из интервала (0, l), причем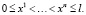 
Задача. Найти функцию u(x, y) со следующими свойствами:
1) 
;
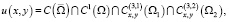
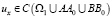2) u(x, y) – регулярное решение уравнения (1) при y ≠ 0;
3) u(x, y) – удовлетворяет краевым условиям
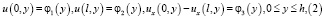
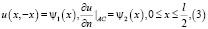
где
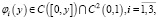
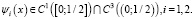
Переходя к пределу в уравнении (1) при y → + 0, получим функциональное соотношение между u(x, 0) = τ(x) и uy (x, 0) = v(x), принесенное из параболической части Ω1 на линию y = 0, в виде
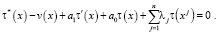(4)
Общее решение уравнения (1) при y < 0 задается формулой
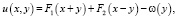(5)
где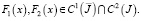 
Удовлетворяя (5) краевым условиям (3), получим систему уравнений
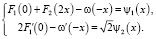
Определим из второго уравнения системы ω(– x):
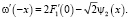
Интегрируя, получим
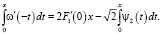
Отсюда, что то же самое
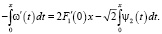
и, окончательно,
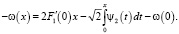
Подставляя ω(– x) в первое уравнение системы, найдем
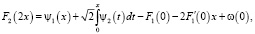
или
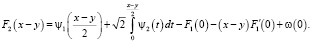
Из (5) будем иметь
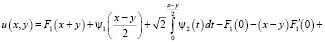
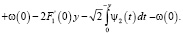
В результате несложных преобразований последнее принимает вид
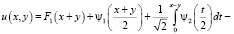
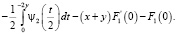(6)
Дифференцируя (6) по x, а затем по y, и вычитая из первого соотношения второе и переходя к пределу при y → – 0, получим функциональное соотношение между τ(x) и v(x), принесенное из гиперболической части Ω2 на линию y = 0 в виде
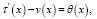(7)
где
Исключая v(x) из (4) и (7), с учетом граничных условий (2), получим для определения τ(x) следующую задачу:
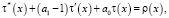(8)
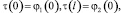
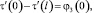(9)
где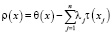 
.
Характеристическое уравнение, соответствующее однородному уравнению
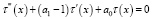(8')
имеет вид
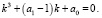(10)
Введем обозначение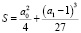 
. Известно [2], что уравнение (10) имеет один действительный и два комплексно-сопряженных корня, если S > 0. Оно имеет три различных действительных корня, если S < 0. При S = 0 все три корня уравнения (10) действительны, причем два из них равны.
Пусть S = 0, т.е.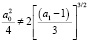 
. В этом случае имеем, что
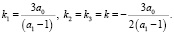
Так как общее решение уравнения (8') в этом случае имеет вид
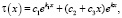
методом вариации постоянных, находим общее решение уравнения (8) в виде
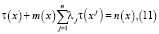
где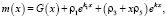 
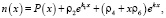
причем, G(x), P(x),ρi – известные функции.
Полагая в равенстве (11) поочередно x = x1, x = x2,…, x = xn, получаем следующую систему алгебраических уравнений относительно τ(x),
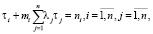(12)
где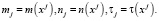 
При выполнении условия
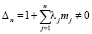(13)
система (12) имеет единственное решение
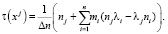(14)
Таким образом, подставляя (14) в (11), находим единственное решение задачи (8), (9). Легко заметить, что τ(0) ≡ 0, если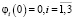 
.
После определения функции τ(x) мы приходим к задаче (2), u(x, 0) = τ(x) в области Ω1. Допустим, что однородная задача имеет нетривиальное решение v(x, y). Положим
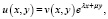(15)
где λ, μ – некоторые постоянные. Для функции v(x, y) получим уравнение
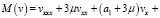
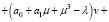
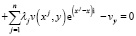
и краевые условия
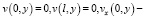
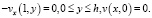(16)
По предположению, в силу (15), эта задача имеет нетривиальное решение v(x, y).
Рассмотрим тождество
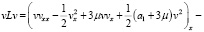
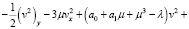
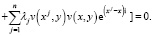
Интегрируя это тождество по области Ω1 и учитывая однородные граничные условия (16) получим
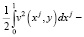
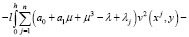
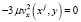(17)
Выберем λ и μ так, чтобы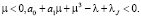 
При таком выборе λ и μ левая часть равенства (17) становится строго положительной, что невозможно, если v(x, y) ≠ 0. Отсюда следует, что v(xj, y) = 0. Отсюда будем иметь, что v(xj, y) ≡ 0 для всех 
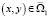, и, согласно (15), u(x, y) ≡ 0 для всех 
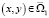. В области Ω2 однородная задача v(x, 0) = 0, 
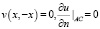для уравнения (1) при y < 0 имеет только тривиальное решение u(x, y) ≡ 0 для всех 
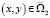. Следовательно, u(x, y) = 0 в Ω2.
Для доказательства существования решения поставленной задачи рассмотрено уравнение
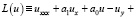
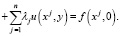(18)
Доказано, что при
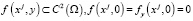
краевая задача
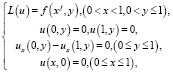(19)
имеет решение.
Существование решения задачи (18), (19) устанавливается с помощью преобразования Лапласа и сведением задачи к системе интегральных уравнений Вольтерра второго рода, относительно следа искомого решения, которая однозначно разрешима.