При исследовании и аппроксимации функций распределения f(x) суммой затухающих экспонент основной целью было получение наилучшей аппроксимации. Аппроксимацией суммой затухающих экспонент наилучшая аппроксимация добивается на участке так называемого «тяжелого» хвоста распределения. Аппроксимация произвольной плотности распределения, описывающая поведение реального потока пакетов (трафика), позволяет аналитически исследовать характеристики сети. В первую очередь существует проблема анализа пакетов при передаче их по сети, зачастую невозможно определить какая максимальная задержка может быть при предоставлении той или иной услуги. Во-вторых, методы, позволяющие исследовать параметры сети на основе статистики передаваемого трафика, как таковые отсутствуют. Одной из главных задач качественной работы и управления сетью, является необходимость заранее контролировать и предугадывать основные характеристики сети: задержку, джиттер, процент потерянных пакетов, пропускную способность и другие.
В работе представлено исследование разработанного алгоритма решения интегрального уравнения (ИУ) Линдли спектральным методом для системы массового облуживания (СМО) типа G/G/1, на основе аппроксимаций с помощью суммы затухающих экспонент. Данная аппроксимация позволяет получить выражение для функции распределения времени ожидания и для среднего времени ожидания пакета в очереди.
Однако при проведении анализа аппроксимации суммой затухающих экспонент возникла проблема в минимизации и сведения к нулю погрешности аппроксимации. Полученные результаты исследования, на примере распределений «тяжелого» хвоста (РТХ), доказывают, что аппроксимация произвольной функции плотности распределения вероятностей, суммой затухающих экспонент целесообразна, так как полученные теоретические априорные оценки погрешности минимальны. Но, на примере функции распределения Вейбулла видно, что осталась не решенной проблема на начальном участке аппроксимации, так как аппроксимация суммой затухающих экспонент плохо описывает исследуемую функцию на участке около нуля.
Задача
Поэтому была предпринята попытка исследования двух участков функции распределения, так называемых «сшитых» функций распределения.
Есть функция Вейбулла f(x), которую аппроксимируем по участкам от (0, x0) и до (x0, ∞), для более точного решения ИУ Линдли, чтобы свести погрешность аппроксимации R(x) → 0.
Плотность функции распределения Вейбулла имеет следующий вид (рис. 1):
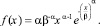 (1)
(1)
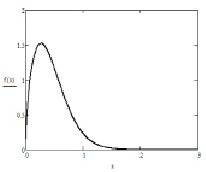
Рис. 1. Функция плотности распределения Вейбулла при α = 1,6 и β = 0,5
Как видно из рис. 2 около нуля возникла проблема с плохой аппроксимацией суммой затухающих экспонент, поэтому будем аппроксимировать функции отдельно и затем «сшивать» их [1].
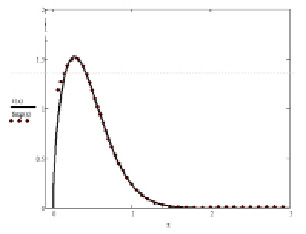
Рис. 2. Сравнение двух плотностей распределения Вейбулла
Представляем аппроксимацию f(x) на участке (0, x0) полиномами:
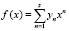
Рассматриваем аппроксимацию f(x) на участке (x0, ∞) суммой затухающих экспонент [2, 3]:
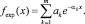
Обязательно необходимо учесть условие нормировки для обеих частей «сшитой» функции.
Рассмотрим «сшитие» функций в одну [1]:
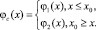
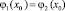 (2)
(2)
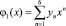
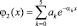
Учитываем условие нормировки
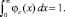
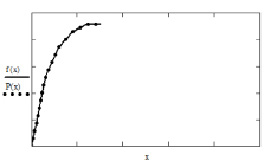
Рис. 3. Аппроксимация функции распределения Вейбулла f(x) на участке (0, x0) полиномами
Необходимо «сшить» две функции φ1(x) и φ2(x) в одну φc(x) а затем найти преобразование Лапласа для решения ИУ Линдли спектральным методом [2, 3].
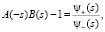 (3)
(3)
где A(s) и B(s) – преобразование Лапласа плотности распределения промежутков времени между поступлениями пакетов и плотности распределения времени обслуживания, соответственно.
Аналитический вид «сшитой» функции:
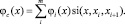
В нашем случае получаем:
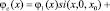
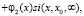
так как функция Вейбулла f(x) существует на отрезке от (0, x0).
В нашем случае примем a = 0, b = ∞ и получим интеграл вида (4)
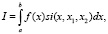
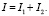 (4)
(4)
Для функции Вейбулла f(x), аппроксимированной полиномами на участке (0, x0), имеем (5):
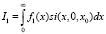 , (5)
, (5)
где 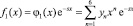 .
.
Для функции Вейбулла f(x), аппроксимированной суммой затухающих экспонент на участке (x0, ∞), имеем (6):
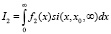 (6)
(6)
где 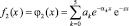 .
.
Пример «сшитых» функций
Рассмотрим случай, когда промежутки времени между поступлениями пакетов имеют распределение Вейбулла с параметрами α = 1,6 и β = 0,5, а промежутки времени обслуживания имеют распределение Парето с параметрами α = 1,5 и β = 1. Экспериментальным путем определяем точку x0, при которой достигается максимальной значение функции распределения Вейбулла при данных параметрах, в этом случае x0 = 0,3.
В соответствии с алгоритмом аппроксимации суммой затухающих экспонент, после получение преобразования Лапласа I «сшитой» функции, необходимо решить ИУ Линдли спектральным методом.
A(s) – преобразование Лапласа плотности распределения промежутков времени между поступлениями пакетов от функции Вейбулла. Преобразование Лапласа от сшитой функции это I = A(s), B(s) – преобразование Лапласа плотности распределения времени обслуживания от функции Парето:
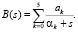
Решаем ИУ Линдли спектральным методом [2] получаем функцию времени ожидания пакетов в очереди W(t):
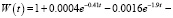
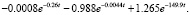
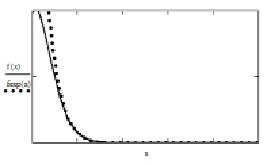
Рис. 4. Аппроксимация f(x) на участке (x0, ∞) суммой затухающих экспонент
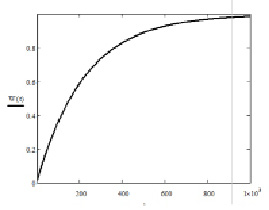
Рис. 5. Функция времени ожидания пакетов в очереди W(t)
Выводы
По данному результату можно сделать вывод, что разбивая на участки аппроксимацию функции распределения, описывающей промежутки времени между поступлениями пакетов, дает ошибку погрешности минимальной. Однако необходимо рассмотреть несколько видов аппроксимации участка около нуля и сравнить наилучшее из решений ИУ Линдли спектральным способом для определения средних характеристик сети.

