Здоровье человека представляет собой социальную ценность. Оно является мощным экономическим, трудовым, оборонным, демографическим, культурным и духовным потенциалом любого общества. Внимание в системе взглядов на здоровье человека должно переместиться с лечения на профилактику болезней и пропаганду способов его достижения, чтобы человек мог радоваться жизни и проявлять заложенный в нем потенциал. Начинать профилактическую работу нужно с раннего возраста человека. Любой гармонично развивающийся процесс обладает симметрией. Метод флуктуирующей асимметрии позволяет оценить стабильность развития любого организма. Показатели флуктуирующей асимметрии можно использовать для разработки перспективных мер профилактики простудных заболеваний у детей.
Новый политический курс состоявшегося государства в области здравоохранения был озвучен Президентом Республики Казахстан Н.А. Назарбаевым в документе «Стратегия Казахстан-2050». «В рамках долгосрочной модернизации национальной системы здравоохранения мы должны на всей территории страны внедрить единые стандарты качества медицинских услуг», – отмечает Н.А. Назарбаев [1]. Одним из ключевых приоритетов становится профилактическая медицина. В предупреждении заболеваний необходимо сделать большой упор на информационно-разъяснительной работе с населением страны. «Мы должны проработать вопрос внедрения новых подходов к обеспечению здоровья наших детей», – говорит Н.А. Назарбаев [1]. Остановимся на статистике ОРВИ и ОРЗ в нашей стране. В среднем человек болеет ими в год два раза, но есть и те, кто болеет четыре-пять раз. По данным ВОЗ 90 % всех болезней приходится именно на простудные заболевания. От ОРЗ, ОРВИ и их осложнений ежегодно умирает на Земле 4 миллиона детей в возрасте до 5 лет. Заболевания ОРЗ, ОРВИ – серьёзная медико-социальная проблема и характеризуется умеренно постоянным ростом. Так в 2015 году среди детского населения в Казахстане в возрасте до 14 лет было зарегистрировано 72632 случая заболеваний на 100000 населения, что на 9,4 % больше, чем аналогичный показатель в 2014 году. Максимум заболевания отмечается в возрасте от 6 месяцев до 6 лет, что составляет 4-6 эпизодов в год. Нельзя не отметить и существенно-материальные потери, наносимые ОРЗ и ОРВИ. Так материальные затраты государства на 1 случай ОРВИ составляют в среднем 6000 тенге, а ежегодный суммарный экономический ущерб от респираторных инфекций в Казахстане оценивается от 25 до 30 млрд тенге. Таким образом, необходимо своевременно проводить мероприятия по профилактике простудных заболеваний у детей.
Цель исследования. Изучение использования метода флуктуирующей асимметрии для оптимизации мер профилактики простудных заболеваний у детей.
Гипотеза. На данном этапе развития профилактической медицины получить систему критериев прогностической оценки предрасположенности отдельных детей к простудным заболеваниям.
Этапы исследований.
– Изучение научной литературы, подбор теоретического материала в библиотеках города и на сайтах Интернета.
– Создание базы данных для расчетных морфологических показателей на основе изучения кожного рисунка ладоней воспитанников детского сада №22 города Тараза.
– Разработка алгоритма выявления и оценки изменений различных форм асимметрии ладоней у детей.
– Окончательная корректировка базы данных проекта и проведение анализа результатов.
Новизна исследований. Получен достаточно объективный, доступный и простой способ исследования информации о склонности ребенка к простудным заболеваниям. Математические расчеты показателей по необходимым признакам могут быть выполнены в электронных таблицах (табличного процессора MS Excel 13) и их можно использовать в дальнейшем для статистического анализа данных.
Результаты работы. Полученные показатели асимметрии кожного рисунка ладоней дают возможность получить критерии ранней диагностики предрасположенности ребенка к простудным заболеваниям, проводить соответствующий мониторинг.
Область практического применения. Идеи и расчеты проекта могут использоваться в детских поликлиниках, детских садах, в медицинской статистике, а также на уроках биологии и математики.
1. Информационное обоснование
Восхищаясь красотой окружающего мира, мы не задумываемся, что лежит в основе этой красоты.
Известный ученый Герман Вейль Клаус Хуго говорил: «Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство» [2].
Об этой закономерности задумывались многие великие люди.
Например, Л.Н. Толстой говорил, стоя перед черной доской и рисуя на ней мелом разные фигуры: «Я вдруг был поражен мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?»[3].
Понятие симметрии проходит через всю многовековую историю человеческого творчества. В своих размышлениях над картиной мира человек с давних пор использовал идею симметрии. По преданию, термин «симметрия» придумал скульптор Пифагор Регийский. Отклонение от симметрии он определил термином «асимметрия».
2. Теоретическое обоснование
Идея симметрии часто является отправным пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна.
2.1 Из истории симметрии
Греческий скульптор Поликлет, очевидно, был первым, кто использовал этот термин ещё в V веке до н. э.
Во время Пифагора понятие симметрии было оформлено достаточно чётко. В то же время он смог подвергнуть его серьёзному анализу и получить результаты универсального назначения. Вот некоторые из них:
1. Для симметрии важны равенство, однообразие и пропорциональность: однообразно (в смысле подчинено какой-либо математической закономерности) располагая равные части, можно построить симметричную фигуру, допустим, квадрат из четырёх равнобедренных треугольников. Если же нарушить закон однообразия в расположении равнобедренных треугольников, то мы получим уже менее симметричную, в пределе – асимметричную, фигуру [4].
2. Пифагорейцы выделили 10 пар противоположностей, среди них «правое» (D) и «левое» (L). Выделим важный момент в учении пифагорейцев. Диалектичность и современность: «мир – это множество, и состоит из противоположностей, то, что приводит противоположности к единству и создаёт всё в космосе, есть симметрия».
Математически строгое представление о симметрии сформировалось сравнительно недавно – в 19 веке.
2.2 Симметрия в математике
Простейшими видами пространственной симметрии являются центральная, осевая, зеркально-поворотная и симметрия параллельного переноса.
Центральная и осевая симметрия
Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1 (рис. 1, а). Точка О считается симметричной самой себе.
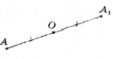
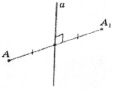
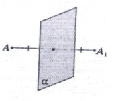
а) б) в)
Рис. 1
Точки А и А1 называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку (рис. 1, б). Каждая точка прямой а считается симметричной самой себе.
Точки А и А1 называется симметричными относительно плоскости a (плоскость симметрии), если плоскость a проходит через середину отрезка АА1 и перпендикулярна к этому отрезку (рис. 1, в). Каждая точка плоскости a считается симметричной самой себе.
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно неё некоторой точки той же фигуры.
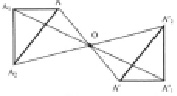
Рис. 2
Если фигура имеет центр (ось, плоскость симметрии), то говорят, что она обладает центральной (осевой, зеркальной) симметрией.
Преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра О, называется центральной симметрией.
Все перечисленные преобразования обладают следующими свойствами:
1) отрезок переходит в равный ему отрезок;
2) угол переходит в равный ему угол;
3) окружность переходит в равную ей окружность;
4) любой многоугольник переходит в равный ему многоугольник и т.д.;
5) параллельные прямые переходят в параллельные, перпендикулярные в перпендикулярные.
Симметрия присутствует и в прошлом, и в будущем. Симметрия – это не только математическое понятие. Его заимствовали из природы.
Слово «симметрия» греческое. Оно означает: «соразмерность, пропорциональность, одинаковость в расположении частей».
2.3 Симметрия растений
На явления симметрии в живой природе обратили внимание ещё в Древней Греции пифагорейцы в связи с развитием учения о гармонии (V век до н.э.). В XIX веке появились единичные работы, посвящённые симметрии в растительном и животном мире. В XX веке усилиями российских учёных В. Беклемишева, В. Вернадского, В. Алпатова, Г. Гаузе было создано новое направление в учении о симметрии – биосимметрика, которое, исследуя симметрии биоструктур на молекулярном и надмолекулярном уровнях, строго описывать внешнюю форму и внутреннее строение любых организмов.
Посмотрим на кленовый лист, он симметричен.
Если прочертить вертикальную прямую вдоль центральной прожилки листа, то получившиеся части листа совпадут друг с другом. И перед нами две половинки – правая и левая! Можно провести опыт и с зеркалом; отражение в зеркале дополнит половину кленового листа до целого. Кленовый лист обладает зеркальной или осевой симметрией.
Зеркальной симметрией обычно обладают листья растений.
Центральную симметрию можно наблюдать на изображении следующих цветов: цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки. В некоторых случаях центральной симметрией обладает и изображение всего цветка ромашки. Весь же цветок обладает центральной симметрией только в случае четного количества лепестков.
Центральная симметрия характерна для различных плодов, ягод и фруктов.
2.4 Понятия асимметрии и её виды
Асимметрия – (греч. a – «без» и «симметрия») – отсутствие симметрии.
Иногда этот термин используется для описания организмов, лишенных симметрии первично, в противоположность дисимметрии – вторичной утрате симметрии или отдельных её элементов.
Понятия симметрии и асимметрии альтернативны. Чем более симметричен организм, тем менее он асимметричен и наоборот. Строение тела многих многоклеточных организмов отражает определённые формы симметрии, радиальную или билатеральную. Небольшое количество организмов полностью асимметричны. В природе и, в частности, в живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Например, симметричные листья растений при сложении пополам в точности не совпадают.
В медицинской литературе рассматривается билатеральная асимметрия, проявляющаяся в парных органах человека (ладони, уши, глаза и т.д). Кроме этого, учитывается направленная асимметрия – проявление неравномерного развития того или иного органа в связи с различной функциональной нагрузкой, выполняемой по частям (развитие асимметрии у прыгунов, гребцов в спорте) [5].
Главными показателями изменений в стабильности развития являются показатели флуктуирующей асимметрии – ненаправленных различий между правой и левой сторонами различных морфологических структур, в норме обладающих билатеральной симметрией [6]. Такие различия обычно являются результатом ошибок в ходе развития организма. При нормальных условиях их уровень минимален, но возрастает при любом стрессовом воздействии, что и приводит к увеличению асимметрии.
Проведя исследования и оценку стабильности развития живых организмов, мы получаем информацию о благополучии среды и в конечном итоге, о ее пригодности для существования человека.
Исследования методом флуктуирующей асимметрии можно проводить на любых билатеральных (симметрично организованных) объектах – будь то животные, растения или человек.
3. Практическое обоснование
Стабильность развития как способность организма к развитию без ошибок и нарушений является чувствительным индикатором состояния природных популяций. Наиболее простой и доступный способ оценки стабильности развития – это определения величины асимметрии двухсторонних морфологических признаков.
Листья у многих растений обладают двусторонней симметрией. При ухудшении качества среды происходит нарушение симметрии в строении листа, что свидетельствует о неблагоприятной экологической обстановке.
Оптимально развивающийся организм в соответствии со своей генетической программой симметричен. Сотрудники лаборатории биоиндикации Калужского государственного педагогического университета имени К.Э. Циолковского нашли универсальный показатель для всех живых организмов – показатель асимметрии [2]. Объектом исследования стал лист березы. Там, где асимметрия березовых листьев наиболее выражена, окружающая среда явно неблагополучна. Используя этот природный барометр, можно легко оценить экологические условия любой местности.
При проведении расследования в работе была использована методика оценки асимметрии листьев для изучения кожного рисунка ладоней детей.
Ладони детей – билатеральный объект, то есть симметрично организованный. На них нанесён кожный рисунок. Ладонная топография представляет собой линии, углы, узоры, которые обладают определённой симметрией. В медицинской литературе есть доказательства, что предрасположенность ребёнка к простудным заболеваниям генетически определена. Одним из проявлений этого генетического фактора, который определяет уровень такой предрасположенности, может быть кожный рисунок на ладонях ребёнка [6]. Флуктуирующая асимметрия может отражать влияние внешней среды на механизмы проявления наследственной информации в процессе жизни человека.
Узоры на поверхности ладони появляются на 10-13-й неделе внутриутробной жизни, начиная с пальцев, постепенно распространяясь на всю поверхность ладони. Учитывая, что каждый узор остаётся неизменённым на протяжении всей жизни и фактически не подвержен влиянию внешней среды, показатели можно учитывать вне зависимости от возраста детей.
3.1 Создание базы данных показателей ладоней воспитанников детского сада № 22 города Тараза
База данных для расчётных морфологических показателей была создана на основе изучения кожного рисунка ладоней 30 воспитанников детского сада № 22 города Тараза.
Для получения информации ладони часто болеющих и эпизодически болеющих детей были сфотографированы. Затем фотографии были увеличены на компьютере и распечатаны на листах формата А-4. С каждой фотографии ладоней снимались показатели с помощью измерительной ленты, транспортира, измерительного циркуля, линейки и лупы.
Изучения данных ладонных показателей проведено с использованием пояснений ладонной топографии по методу Камминса и Мидло.
Данные измерений были занесены в таблицы № 1 и № 2. Измерения параметров ладонных показателей эпизодически болеющих детей и измерения параметров ладонных показателей часто болеющих детей. Изучено 5 ладонных показателей кожного рисунка на левой и правой руке ребенка.
3.2 Вычисление интегральных показателей флуктуирующей асимметрии для различной категории детей
Величину асимметричности мы оцениваем с помощью интегрального показателя – величины среднего относительного различия на признак (среднее арифметическое отношение разности к сумме промеров левой и правой руки, отнесенное к числу признаков).
Подобные вычисления мы производим по каждому признаку (от 1 до 5). Все результаты фиксируем в таблице № 3.
Для вычисления ладонных показателей всех детей из категории эпизодически и часто болеющих применили формулы программы Ехсеl 2013.
3.3 Оценка изменений различных форм асимметрий ладоней у детей
В результате проведённых исследований была установлена степень нарушения стабильности развития организма детей по отношению к заболеваниям ОРЗ и ОРВИ.
Величина показателя асимметрии в исследуемых группах детей
|
Категории детей |
Величина показателя асимметрии |
|
Эпизодически болеющие дети |
0,011852 |
|
Часто болеющие дети |
0,039649 |

а) б)
Рис. 3. Схема ладонной топографии (А), ладонных полей, трирадиусов, линий и узоров (В) (по Cummins, Midlo, 1961; Л.П. Сергиенко, В.П. Кореневич, 1997)
Предполагается, что нарушение функционирования систем адаптации организма ребёнка, которое проявляется частыми респираторными заболеваниями, сопряжено с механизмом развития кожного рисунка и его формированием.
Имеется перспектива продолжить изучение ладоней ребёнка, так как их топография многогранна. Так можно рассмотреть окончания главных ладонных линий на полях ладоней, продолжить измерение угловых и получить дополнительную информацию, используя бимануальную асимметрию.
Данные таблицы дают определённое представление о предрасположенности отдельной категории детей к простудным заболеваниям.
Заключение
Данный проект показывает практическое улучшение флуктуирующей асимметрии для профилактики простудных заболеваний у детей.
Проведены расчёты для наиболее информативных показателей кожного рисунка ладоней детей. Вся работа подчинена практическому характеру научного исследования. Расчёты показателей по необходимым признакам могут легко поддерживаться информационно – коммуникативными технологиями в программе МS Ехсе1.
С помощью флуктуирующей асимметрии задачи профилактики простудных заболеваний могут решаться в реальном масштабе времени и допускают адаптации к частым случаям.
Профилактическая работа может быть интерактивно спланирована с одновременным оцениванием затрат на оказание объёма медицинской помощи.
Идеи работы и расчёты могут использоваться в педиатрии, на уроках биологии и математики, в медицинском мониторинге и статистике.

