В геоинформатике имеет место интеграция данных и технологий [1]. Однако она может быть двух видов: с сохранением пространства и с увеличением пространства параметров. Свойства пространственных объектов также могут быть описаны некими множествами [2]. Это дает возможность объединять эти свойства, получая на выходе новые знания [3]. Однако часто теорию множеств применяют односторонне. Это обусловлено тем, что при анализе элементов упускают из вида свойства этих элементов, а при анализе свойств, упускают отношения элементов множества. Рассмотрим два вида интеграции. Интеграция с сохранением пространства параметров. Пусть заданы два множества А, В с общими p и частными x, y свойствами. При этом существуют частные одинаковые свойства xt. Формальное атрибутивное (признаковое) описание таких множеств имеет вид: A(p, xt, x), B(p, xt, y). Результатом интеграции с сохранением пространства параметров будет множество D, основанное на пересечении множеств
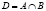
С описанием D(p, xt). При такой интеграции частные x, y свойства удаляются. Если говорить об элементах «e» нового множества D(p, xt), то для них будет противоположная ситуация. Элементы совокупного множества eD определяться как объединение
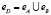
В результате такой интеграции количество элементов увеличилось, а количество свойств уменьшилось. В результате такой интеграции новое множество является более однородным по свойствам, частности исключены. Это приводит к снижению избыточности. Избыточность состоит в том, что частные одинаковые свойства xt присутствуют в обеих множествах дважды. При интеграции одно из xt исключатеся. В результате такой интеграции функции имеют такое же количество как до интеграции. Новое множество является более однородным по свойствам, частности исключены.
Интеграция с увеличением пространства параметров строится как Декартово произведение. Пусть заданы три множества А, В, С, такие, что каждое множество обладает только своими свойствами или признаками: A(x), B(y), C(z). Результатом интеграции с увеличением пространства параметров будет множество D(x, y, z). В результате такой интеграции новое множество является более размерным в пространстве параметров. Количество признаков увеличилось и увеличилось количество элементов. Такая интеграция увеличивает размерность пространства параметров и позволяет работать с функциями с большим числом переменных. Примером такого множества является Декартова система координат.

