Самое распространённое вещество на Земле – морская вода – представляет собой сложный раствор электролитов. Многие её физические и химические свойства изучены давно и тщательно, в том числе и акустические. Однако исследование характера распространения упругих волн ограничивалось прежде звуковым и ультразвуковым диапазоном частот.
В этой работе экспериментально исследована скорость и поглощение гиперзвука в воде из акватории Черного моря на частоте 4,5 ГГц. Его длина волны сравнима с размерами ионных кластеров, существующих в морской воде, поэтому возможно интенсивное взаимодействие упругих волн со средой, в которой они распространяются.
Гиперзвук (ГЗ) изучался по спектрам рассеянного света [8]. В жидкостях, независимо от их природы, всегда существуют спонтанные звуковые волны различных частот, которые возбуждаются в результате теплового движения молекул. Когда на жидкость падает свет с длиной волны λ, он рассеивается под углом θ на тех звуковых волнах, длина волны Λ которых удовлетворяет условию Брэгга 2Λsin(θ/2) = λ. В результате чего частота света испытывает доплеровское смещение, и в спектре рассеянного света возникают две линии – компоненты Мандельштама – Бриллюэна (КМБ). Их смещение ν относительно линии возбуждающего света пропорционально скорости звуковой волны υ, что и позволяет рассчитывать её на частоте, равной смещению КМБ:
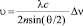, (1)
где n – показатель преломления среды; с – скорость света. При угле рассеяния θ = 90 ° частота звука, вызывающего КМБ, составляет несколько гигагерц.
Высокочастотная волна, распространяясь в жидкости, заметно затухает, что приводит к уширению КМБ на величину
Г = αυ, (2)
где α – амплитудный коэффициент поглощения звука.
Эксперимент выполнялся на установке, в которой в качестве источника возбуждающего света служил гелий-неоновый лазер мощностью излучения 30 мВт на длине волны λ = 633 нм. Спектральное разложение света, рассеянного под углом θ = 90 °, осуществлялось сканируемым интерферометром Фабри – Перо. Фотодетектором служил охлаждаемый ФЭУ-79, работавший в одноэлектронном режиме. Аппаратная функция установки хорошо аппроксимировалась функцией Гаусса, и её влияние учитывалось при определении истинной ширины Г КМБ. Подробно установка описана в работе [4].
Для обработки спектров нужно знать ещё вспомогательные величины: показатель преломления n воды, коэффициент сдвиговой вязкости η и плотность ρ. Они все измерялись при разных температурах соответственно рефрактометром ИРФ-23, вискозиметром Хепплера и денсиметром.
Для сравнения результатов гиперзвуковых измерений в той же воде ещё исследована температурная зависимость скорости ультразвука (УЗ) частотой 1,4 МГц. Измерение производилось с помощью прибора УС-13И эхо-импульсным методом. Скорость УЗ и ГЗ определялась с точностью до 0,7 %, поглощение гиперзвука – несколько хуже: до 4–5 %.
Перед проведением опытов морская вода тщательно фильтровалась с помощью стеклянного фильтра с размерами пор 10 мкм, а чистая вода – дважды перегонялась под вакуумом.
Скорость распространения ГЗ в морской воде исследована в интервале температур от 2,9 до 95,8 °С, ультразвуковые измерения проведены от 10 до 90,6 °С. Частота ГЗ на три порядка выше УЗ и составляла около 4,5 ГГц, причём с температурой воды она несколько изменялась. Результаты исследования показаны на рис. 1. Здесь же для сравнения приведены ультразвуковые данные из [1] и наши измерения гиперзвука в чистой воде.
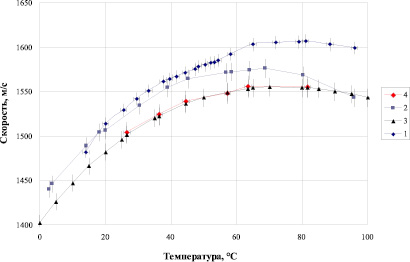
Рис. 1. Температурная зависимость скорости ультра- и гиперзвука в воде: морская вода: 1 – УЗ, 2 – ГЗ; чистая вода: 3 – УЗ(ν = 0,75–70 МГц), 4 – ГЗ
Особенностью распространения акустических волн в чистой и морской воде является то, что с ростом температуры скорость сначала увеличивается, достигая максимума, а затем снижается. В чистой воде максимум соответствует 74 °С, и кривая υ(t) имеет параболическую форму. Это характерно только для воды и простых водных растворов электролитов. В других жидкостях скорость звука монотонно убывает с нагреванием. Максимум скорости гиперзвука в чистой воде может быть объяснен на основе ее двуструктурной модели, в которой рассматривается равновесие между льдоподобной и более плотноупакованной структурами. С повышением температуры возрастает концентрация плотноупакованной структуры, что приводит к уменьшению сжимаемости. Однако с ростом температуры увеличивается среднее расстояние между молекулами в каждой структуре, что увеличивает сжимаемость. Эти две противоположные тенденции приводят к минимуму сжимаемости, и, следовательно, к максимуму скорости звука.
В морской воде скорость упругих волн выше, чем в чистой; температурная кривая скорости смещена на 10 °С в сторону низких температур. Это объясняется тем, что ионы нарушают преобладающие структуры и упорядоченность растворителя. Они как бы стремятся создать новую, более компактную структуру, в которой молекулы воды вблизи каждого иона ориентированы в его электрическом поле. Если перестроить график в координатах (υmax – υ) от (tmax – t)2, то экспериментальные точки хорошо ложатся на прямую линию во всей температурной области. Это означает, что параболичность кривой скорости ГЗ в морской воде не нарушается.
Однако самое существенное различие в характере распространения УЗ и ГЗ заключается в следующем. При температуре морской воды до 60 °С их скорости практически одинаковые – небольшое отличие на рис. 1 находится в пределах погрешности эксперимента. При более высокой температуре скорость ГЗ оказывается меньше скорости УЗ, т.е. начинает проявляться редкое явление – отрицательная дисперсия акустических волн. Впервые оно было надежно обнаружено нами сначала в водном растворе сульфата магния [5], а затем в растворе хлористого аммония.
Теория этого явления была развита [3, 6] задолго до его экспериментального обнаружения. В работе [3] рассматривалась дисперсия скорости звука, обусловленная межмолекулярным взаимодействием, но не связанная с релаксацией сдвиговой и объёмной вязкости. В работе В.Л. Гинзбурга [3] исследовалось уравнение Навье – Стокса, составленное во втором приближении. При этом принималось, что поглощение звука очень мало, и поэтому влияние вязкостей на дисперсию не рассматривалось, а выявлялись другие причины.
Обе теории приводят к результату, который можно выразить формулой:
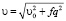, (3)
где υ0 – скорость звука на низкой частоте; f – величина, характеризующая межмолекулярное взаимодействие; q = 2π/Λ – волновое число звуковой волны. Эту формулу можно переписать следующим образом:
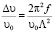. (4)
Знак дисперсии υ = υ – υ0 скорости определяется знаком f, а он зависит от характера межмолекулярного взаимодействия. В молекулярном кластере взаимодействующих друг с другом частиц, f < 0, и дисперсия υ будет отрицательной. Величину υ можно связать с размером кластера r, положив очевидное соотношение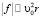 
. Учитывая это, формулу (4) можно записать иначе:
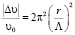. (5)
Это соотношение показывает, что в ассоциированных жидкостях при больших размерах кластеров, должна проявляться всегда отрицательная дисперсия. Однако в эксперименте она обнаруживается очень и очень редко, что, по-видимому, связано с релаксационными процессами, приводящими к положительной дисперсии, которая и вуалирует в той или иной степени отрицательную.
В чистой воде надёжно установлено, что оба вида дисперсий скорости отсутствуют (см. рис. 1). Поскольку водные растворы электролитов сильно ассоциированы, в них имеются условия для проявления отрицательной дисперсии, что и наблюдается в морской воде при t > 60 °С. С ростом температуры величина υ увеличивается, что, по-видимому, связано с увеличением подвижности частиц, образующих ионные кластеры. Из наших данных следует, что при t = 86 °С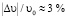 
. Из этих данных оценка размеров кластеров по формуле (5) дает значение r ~ 10 нм. При таких условиях должна сильно измениться индикатриса рассеяния света – из симметричной она должна стать вытянутой вперед. Однако исследование угловой зависимости интенсивности рассеянного света в природной воде – задача не из легких, так как практически невозможно произвести её глубокую очистку, а посторонние взвеси будут искажать релеевское рассеяние. Такие исследования можно выполнить в «морской» воде, приготовленной искусственно.
Кроме скорости акустических волн, нами был определен из ширины КМБ коэффициент поглощения ГЗ при комнатной температуре в морской воде. На рис. 2 в логарифмическом масштабе по обеим осям представлена частотная зависимость отношения коэффициента поглощения упругих волн к квадрату их частоты α/ν2.
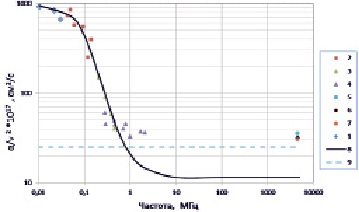
Рис. 2. Частотная зависимость поглощения упругих волн в морской воде: 1–5 – Гз, 5 –7 – Уз
Разными значками показано поглощение ультразвука, взятого из разных литературных источников [9–12], и наши результаты для ГЗ. При изменении частоты УЗ от 10 кГц до 2,8 МГц отношение α/ν2 уменьшается приблизительно в 30 раз, однако при росте частоты вплоть до 4,5 ГГц оно практически не изменяется, и на этой частоте равно (35,5 ± 1,8)·10–17 с2см–1. На рисунке для сравнения приведено α/ν2 в чистой воде: поглощение упругих волн одинаково во всем изученном диапазоне частот. В морской воде поглощение на низких частотах в 40 раз больше, чем в чистой воде, а в гигагерцовом диапазоне превышает лишь в 1,4 раза. Есть мнение [9], что избыточное поглощение на низких частотах обусловлено, в основном, MgSO4, концентрация которого в морской воде около 0,03 моль/л. В это поглощение вносят вклад также и другие 2-х валентные электроны. Принятая в настоящее время интерпретация избыточного поглощения предполагает, что оно связано с нарушением равновесия под действием упругой волны, включающим ступенчатое удаление молекул из пространства между партнерами ионной пары. Время релаксации τ этого процесса можно определить из эксперимента. Величина общего поглощения α/ν2, обусловленного сдвиговой η и объёмной η’ вязкостью согласно релаксационной теории Мандельштама – Леонтовича определяется частотой ν воздействия на среду [8]:
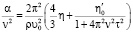. (6)
Здесь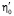 
– статическое значение коэффициента объёмной вязкости. Подставляя в (6) экспериментальные α/ν2 для двух частот и решая получившиеся уравнения, можно найти, что 
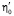= 1,49 Пз и τ = 1,7 мкс. Величины η, ρ и υ0, входящие в (6), измерены нами на опыте. Если 
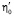и τ подставить снова в (6), то можно вычислить α/ν2 для всего частотного диапазона. На рис. 2 это показано в виде сплошной линии. На низких частотах расчёт хорошо согласуется экспериментом с морской водой из разных акваторий, а на средних и высоких частотах наблюдается существенная разница. Следовательно, поглощение акустических волн в морской воде простым соотношением (6) не описывается. На высоких частотах проявляется ещё некоторое добавочное поглощение. Чтобы выяснить, с чем оно связано, были составлены три водных раствора: MgSO4 (C=0,028М); MgSO4 (C=0,028М) + NaCl (C=0,42М) и MgSO4 (C=0,028М) + NaCl (C=0,42М) + KCl (C=0,01М), с таким же соотношением компонент, как и в природной морской воде. Поглощение гиперзвука в растворе сульфата магния α/ν2 = 25,8·10–17 с2см–1, что немного больше, чем в чистой воде. В двух- и трёхкомпонентном растворе величина α/ν2 составляет 31,7·10–17 и 30,0·10–17 с2см–1 соответственно, что ближе к значению α/ν2 в морской воде. Таким образом, добавочное поглощение звука на высоких частотах, по-видимому, связано с 1–1 валентными ионами; на малых частотах их роль в поглощении незначительна [7].