«Одной из основных задач теории чисел является поиск доказательства гипотезы Гольдбаха. Гольдбах (1690-1764) сам по себе не оставил никакого следа в истории математики: он прославился только проблемой, которую он предложил Эйлеру в письме, относящемся к 1742 г. Он обратил внимание на тот факт, что ему всегда удавалось представить любое четное число (кроме 2, которое само есть простое) в виде суммы двух простых. Например, 4 = 2 + 2, 6 = 3 + 3, 8 = 5 + 3, 10 = 5 + 6, 12 = 5 + 7, 14 = 7 + 7, 16 = 13 + 3, 18 = 11 + 7, 20 = 13 + 7, … , 48 = 29 + 19, … , 100 = 97 + 3, и т.д. Гольдбах спрашивал у Эйлера, может ли он доказать, что такого рода представление возможно для всякого четного числа, или же напротив, сможет указать пример, опровергающий такое предположение. Эйлер так и не дал ответа; не дал его никто и в дальнейшем» [1, с. 58-59].
Поиск доказательства, конечно же, интересное и занимательное занятие, т.к. доказательство позволит на сто процентов быть уверенным в существовании этого удивительного свойства, но … не более того. Более важным, с точки зрения познания, представляется выявление причины его возникновения и анализ этой гипотезы с целью выяснения того, что она может дать для теории чисел, ведь гипотеза Гольдбаха не так проста, как кажется на первый взгляд.
Во-первых, гипотеза Гольдбаха позволяет установить максимальное расстояние между двумя соседними простыми числами:
Следствие гипотезы Гольдбаха. Для любого простого числа Pi следующее простое число Pi + 1 удовлетворяет условию: Pi + 1 < Pi + Pi-1.
Действительно, если бы число Pi + 1 не удовлетворяло указанному условию, тогда число 2N = Pi + Pi-1 + 2 невозможно представить в виде суммы двух простых, что противоречит гипотезе Гольдбаха.
Это свойство, в несколько иной трактовке, обнаружил Бертран, сформулировав его в виде постулата: для любого натурального числа N существует простое число P, удовлетворяющее условию N < P < 2N-2. Доказательство этого постулата было найдено П.Л. Чебышевым в 1859 году [2].
Во-вторых, любое четное натуральное число можно представить не только в виде суммы, но и в виде разности двух простых. Например: 2 = 1 + 1 = 3 – 1 = 5 – 3 = 7 – 5 = = …, 4 = 1 + 3 = 5 – 1 = 7 – 3 = 17 – 13 = …, 6 = 1 + 5 = 3 + 3 = 7 – 1 = 11 – 5 = 13 – 7 = …, 8 = 1 + 7 = 3 + 5 = 13 – 5 = 19 – 11 = … и т.д. В связи с этим гипотезу Гольдбаха можно обобщить:
Обобщенная гипотеза Гольдбаха. Любое четное натуральное число можно представить в виде: 2N = Pj ± Pi, где Pj > Pi – простые числа.
Так все-таки, в чем же кроется причина этого свойства? Чтобы разобраться в этом вопросе, напомним, что существуют так называемые простые числа-близнецы, т.е. простые числа p и q, удовлетворяющие условию: p-q = 2, также существуют двоюродные простые числа – p-q = 4 = 2*2, троюродные – p-q = 2*3, четвероюродные – p-q = 2*4 и т.д. Анализ вопроса о том, какие простые числа в каких «родственных отношениях» находятся между собой, позволил обнаружить, что ВСЕ простые числа, кроме двойки, являются в той или иной степени «братьями», т.е. каждое простое число является «братом» в какой-то мере всем другим простым числам. Это объясняется существованием чисел вида:
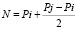 (*)
(*)
где Pj > Pi – простые числа, а число (Pj-Pi)/2 как раз и определяет степень родства, т.е. числа (*) находятся как раз посредине между Pi и Pj.
При рассмотрении выражения (*), возникает вопрос: какие натуральные числа представимы в таком виде? Проверка на первых пяти сотнях простых числах показала, что все натуральные числа представимы в таком виде. Поэтому, в качестве предположения, можно выдвинуть гипотезу:
Гипотеза (гипотеза о натуральных числах). Любое натуральное число представимо в виде (*).
Умножив обе части выражения (*) на два, получим гипотезу Гольдбаха.
Верным также является и обратное утверждение, т.е.:
Если гипотеза Гольдбаха справедлива, то и гипотеза – справедлива.
Действительно, если для любого натурального числа N справедливо утверждение, что 2N = Pi + Pj, где Pi<Pj – простые числа, тогда получим:
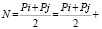
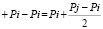
т.е. любое натуральное число представимо в виде (*), что говорит о равнозначности гипотезы Гольдбаха и гипотезы ?.
Выражение (*) можно несколько упростить, перенося Pi в левую часть и получая в левой части, пусть и меньшее, но все же натуральное число. В связи с этим, гипотезу можно сформулировать следующим образом:
Упрощенная гипотеза . Любое натуральное число представимо в виде:
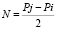
т.е. существуют пары простых чисел любой степени родства, так, среди первых 561 простых чисел 107 пар являются числами-близнецами, 208 – троюродных, а 105-юродных – 304.
Теперь, умножая обе части этого выражения на два, получим обобщение гипотезы Гольдбаха.
Гипотеза может представлять интерес для криптографии. В некоторых ассиметричных схемах шифрования в качестве основы открытого ключа используются числа, представляющие произведение двух очень больших простых чисел, а задача факторизации (разложение чисел на простые множители) представляет собой достаточно трудноразрешимую задачу по затратам времени. «В последние годы благодаря применению тонких методов теории чисел и алгебраической геометрии было разработано несколько эффективных алгоритмов факторизации <…> Среди последних достижений в этой области можно упомянуть об успехе Ленстры и Монасси, разложивших в июне 1990 года 155-разрядное число на три простых. Для этого они использовали 1 000 объединенных ЭВМ и шесть недель их машинного времени. Вычисления проводились с помощью алгоритма английского математика Дж. Полларда. Ленстра и Монасси считают, что в настоящее время (1991 г.) можно в течение года разложить новые классы целых чисел длиною до 155 разрядов, затратив на это 200 млн долларов» [3, с. 52-53]. Если в качестве основы открытого ключа использовать достаточно большое число, то количество вариантов разложение его по выражению (*) на два простых, будет существенно большим. Если же в выражении (*) дополнительно использовать ещё и отрицательные простые числа, то поиск секретного ключа становится теоретически неразрешимой задачей в силу бесконечности пар простых положительных и отрицательных чисел для представления любого числа. К примеру, число 5, с использованием только положительных простых чисел, можно представить единственным образом: 5 = 3 + (7-3)/2, тогда как при использовании еще и отрицательных простых чисел, получаем бесконечное множество представлений:
5 = – 1 + (11 – ( – 1))/2 = – 3 + (13 – – ( – 3))/2 = – 7 + (17 – ( – 7))/2 = – 13 + (23 – – ( – 13))/2 = – 19 + (29 – ( – 13))/2 = … и т.д. В качестве дополнительной меры секретности можно применять так называемое двойное кодирование, т.е. предварительно перед шифрованием каким-то образом перемешать символы исходного текста для того, чтобы в случае случайного использования секретного ключа, расшифрованный текст выглядел «абракадаброй».

