Россию ждет затяжная стагнация, если не будет реформ, – так оценивают нынешнее состояние большинство специалистов. Минфин просчитал основные варианты развития российской экономики на период до 2030 г. Представляется целесообразным, наряду с консервативным, инерционным и инновационным вариантами развития, рассмотреть также и оптимальный. В этой связи необходимо обратиться к теории оптимального управления. Под управлением понимается прямое воздействие на систему, направленное на достижение заданного результата. В этом отличие управления от регулирования, которое осуществляется на основе сравнения регулируемого (выходного) показателя с задающим (входным).
Под оптимальным управлением понимается выбор из многих возможных такого варианта управления, который по заданному критерию является оптимальным [4].
Поведение любой нелинейной многосвязной системы описывается следующими уравнениями движения [2]:
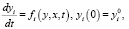 i = 1,…,п, (1)
i = 1,…,п, (1)
где у – вектор фазовых координат, задающий состояние системы; х – вектор внешних (входных) задающих и (или) возмущающих воздействий на систему; 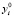 – начальные значения фазовых переменных.
– начальные значения фазовых переменных.
Если возмущающие воздействия пренебрежимо малы, некоторые из задающих воздействий становятся управляющими, а другие являются заданными известными функциями времени, то приходим к следующим уравнениям для управляемой динамической системы:
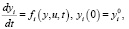 i = 1,…,п, (2)
i = 1,…,п, (2)
где и – вектор управляющих параметров, u∈U; U – область допустимых значений управляющих параметров.
Управляющая траектория (управление) u(t) называется допустимой, если она кусочно-непрерывна, в точках разрыва непрерывна слева:
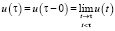 , и кроме того при любом t u(t)∈U.
, и кроме того при любом t u(t)∈U.
Если задан закон управления, т. е. определена допустимая управляющая траектория u(t), то уравнения для фазовых переменных принимают вид:
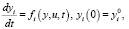 i = 1,…,n. (3)
i = 1,…,n. (3)
тем самым при любых начальных условиях у(0) = y0 однозначно определяется решение.
В качестве критерия оптимальности выбирается некоторый функционал от фазовой и управляющей траекторий, который подлежит максимизации (минимизации). Необходимые условия для решения такой задачи дает принцип максимума Понтрягина.
Принцип максимума Понтрягина
Принцип максимума Понтрягина применяется к общей задаче управления, имеющей вид [3]:
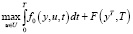 (4)
(4)
где 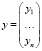 – вектор-столбец фазовых переменных, определяющих состояние динамической системы;
– вектор-столбец фазовых переменных, определяющих состояние динамической системы;
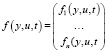 – вектор-столбец правых частей уравнений системы;
– вектор-столбец правых частей уравнений системы;
y0, уT – начальное и конечное значения вектора состояния;
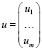 – вектор-столбец управляющих параметров;
– вектор-столбец управляющих параметров;
U – область возможных значений управляющих параметров;
f0 (y, u, t) – подынтегральная функция критерия управления.
Функции f (у, и, t), F (уT, Т) – непрерывны и дифференцируемы по каждому аргументу. Если определено уравнение u(t), то однозначно при заданном начальном условии у(0) = y0 определена траектория системы y(t). Траекторию системы, соответствующую оптимальному управлению u*(t), назовем оптимальной и обозначим y*(t).
Как известно, задача нелинейного программирования сводится к поиску седловой точки функции Лагранжа [1]. Именно этот подход применяется и для решения задачи (4). Роль переменных выполняют управляющие переменные и, ограничениями служат дифференциальные уравнения для фазовых переменных
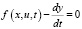 , (5)
, (5)
а роль функции цели выполняет функционал
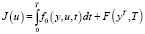 . (6)
. (6)
Построим функцию Лагранжа для этой задачи:
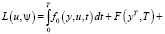
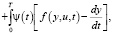 (7)
(7)
где 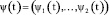 – вектор-строка множителей Лагранжа, которые в этой ситуации называются сопряженными переменными (по отношению к фазовым).
– вектор-строка множителей Лагранжа, которые в этой ситуации называются сопряженными переменными (по отношению к фазовым).
Подынтегральная функция в последнем интеграле выражения (7) – это матричная форма записи скалярного произведения вектора-строки ψ(t) на вектор-столбец 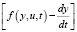 :
:
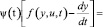
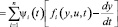
Седловая точка (точнее, траектория) u*(t), у*(t) определяется как решение неравенства
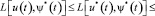
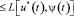 (8)
(8)
Если u*(t), 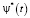 – седловая точка, то u*(t) – оптимальное управление, т.е. решение задачи (8).
– седловая точка, то u*(t) – оптимальное управление, т.е. решение задачи (8).
В самом деле, правое неравенство (8)
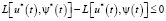 , (9)
, (9)
тем самым на оптимальной траектории выполнены уравнения системы
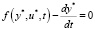
(если бы в некоторых точках уравнения системы не выполнялись, то подбором функций можно было бы сделать неравенство (9) строго большим нуля, т.е. придем к противоречию). Рассмотрим левое неравенство (8), из него следует:
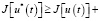
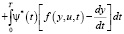
поэтому для всех управлений u(t), для которых выполняются уравнения системы (5),
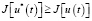 .
.
т.е. действительно u*(t) – оптимальное решение (управление) задачи (4). При этом максимальное значение критериального функционала задачи (4) равно значению функции Лагранжа в седловой точке.
Необходимые условия оптимальности (принцип максимума)
Итак, если u*(t), ψ*(t) – седловая точка, то u*(t) – оптимальное решение задачи (4). Поэтому необходимые условия существования седловой точки являются одновременно и необходимыми условиями максимума задачи (4).
Если сопряженные переменные получили бесконечно малые приращения ∆y, то согласно выражению (7) функция Лагранжа получила бесконечно малое приращение:
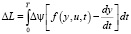
Поскольку u*(t), ψ*(0 – седловая точка, то, согласно правому неравенству (8), в этой точке функционал L(u*, ψ) достигает минимума по ψ, поэтому для любого бесконечно малого приращения ∆ψ в окрестности этой точки ∆L = 0, и тем самым
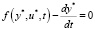
т.е. для управления u*(t) и соответствующей ему фазовой траектории y*(t) выполняются уравнения системы.
Остальные необходимые условия оптимальности следуют из левого неравенства для седловой точки.
Прежде всего путем интегрирования по частям функция Лагранжа преобразуется к виду
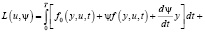
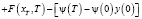
Первые два слагаемых под знаком интеграла называются функцией Гамильтона:
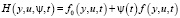 , (10)
, (10)
поэтому функция Лагранжа преобразуется к виду
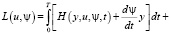
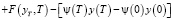 . (11)
. (11)
Если управление u(t) получило приращение ∆u(t), то фазовая траектория изменилась с у(t) на y(t) + ∆y(t), а функция Лагранжа получила приращение:
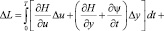
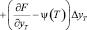 , (12)
, (12)
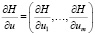 ,
, 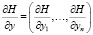
Поскольку для существования максимума необходимо ∆L = 0 при любых ∆и, то, приравняв нулю (12), получаем необходимые условия максимума:
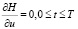 (13)
(13)
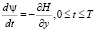 (14)
(14)
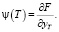 (15)
(15)
Условия (13) – это условия существования локального максимума функции Гамильтона без учета ограничений на управляющие параметры. Если такие ограничения есть, то условия (13) заменяются следующими:
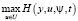 . (16)
. (16)
Согласно условию оптимальности (16) функция Гамильтона в любой момент t либо должна принимать свой внутренний (локальный) максимум, и тогда должно выполняться условие 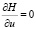 , либо максимум достигается на границе, тогда
, либо максимум достигается на границе, тогда 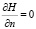 , где n – направление нормали к границе.
, где n – направление нормали к границе.
Из выражения для функции Гамильтона (10) видно, что 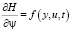 , но
, но 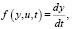 поэтому
поэтому 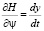 .
.
Таким образом, процедура применения принципа максимума задаче (4) состоит в следующем.
Сначала вводятся п сопряженных переменных затем строится функция Гамильтона: 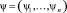 после чего определяются функции u(t),
после чего определяются функции u(t), 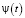 , y(t), удовлетворяющие условиям:
, y(t), удовлетворяющие условиям:
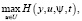
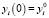 ,
,
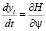 ,
,
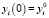 , j = 1,…,n,
, j = 1,…,n,
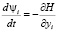 ,
,
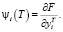
Если кроме уравнений движения есть и другие ограничения, то они обычным образом включаются в функцию Лагранжа, а, следовательно, и в функцию Гамильтона [5].
Принцип максимума дает лишь необходимые условия оптимальности. Действительно, оптимальная траектория состоит из некоторых участков управляющих траекторий, определенных по этому принципу.
Выводы
Если ничего не делать, в том числе со структурой бюджета, то сценарий долгосрочной стагнации может реализоваться. Но расчеты показывают, что наиболее вероятным является другой, оптимально-целевой сценарий развития, который позволит экономике выйти на темпы роста в 2-3 %. Ключевое условие для этого – структурные изменения в экономике – повышение отдачи на капитал за счет роста производительности труда, опережающего рост зарплат, и, как результат, увеличение доли инвестиций в ВВП. Такой подход требует повышения гибкости рынка труда, мобильности работников, вложений в их переобучение. В этом случае экономика сможет преодолеть экономический спад уже в 2018 г., увеличиваясь к 2030 г. на 44 %.

