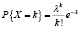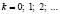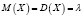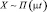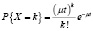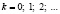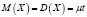Переход на компетентностно-ориентированное образование заключается в требованиях формировать в результате обучения как профессиональные, так и общекультурные компетенции. Важным условием достижения результативности в формировании компетенций является междисциплинарная интеграция. Междисциплинарная интеграция создает возможности для формирования у учащихся целостной картины взаимосвязанного и взаимозависимого мира. Студент, многократно применяя знания по каждой изучаемой или изученной дисциплине за рамками самой дисциплины, в новых условиях, формирует умение применять знания и в профессиональной деятельности [5].
Целью данной работы является теоретическое обоснование и экспериментальная апробация средств междисциплинарной интеграции(на примере теории вероятностей и экономических дисциплин), способствующих реализации компетентностного подхода.
Интегрированное занятие – это особый тип занятия, объединяющего в себе обучение одновременно по нескольким дисциплинам при изучении одного понятия, темы или явления. Проанализируем основные функции интегрированных занятий в процессе обучения математике, и выделим действия, которые необходимо включить в процесс их подготовки.
Мировоззренческая функция. Содержание образования должно обеспечивать формирование у обучающегося адекватной современному уровню знаний и уровню образовательной программы (ступени обучения) научной картины мира. Система знаний о мире формируется у студентов при изучении всех дисциплин. Каждая дисциплина рассматривает факты и явления реальной действительности односторонне. В связи с этим студенты испытывают трудности в восприятии понятий и представлений о реальном мире как системе в целом, в их взаимосвязи. Интегрированные занятия способствуют формированию целостного взгляда на мир, пониманию сущностных взаимосвязей явлений и процессов [3].
Мотивационная функция. Интегрированные занятия активизируют учебно-познавательный процесс, являются средством развития интереса учащихся к предмету и его практическим приложениям.
Развивающая функция. Интегрированные занятия являются эффективным средством организации проблемного обучения, содействуют развитию творческих способностей учащихся, формированию универсальных учебных действий.
Общекультурная функция. Интегрированные занятия расширяют кругозор учащихся, способствуют формированию представлений о математической науки как части общечеловеческой культуры. Повышение общематематической культуры естественным образом содействует повышению и профессиональной и общей культуры.
Реализация всех выше указанных дидактических функций способствует также успешному формированию конкретных математических знаний.
В процесс подготовки интегрированных занятий по математике важно включить следующие действия:
1) выделить проблемы в обучении, которые можно решать включением в процесс обучения интегрированных занятий;
2) в зависимости от выделенных проблем, а также в соответствии с целями образования и целями конкретного занятия выбрать вспомогательные дисциплины;
3) совместно с преподавателем вспомогательной дисциплины отобрать содержание занятия.
4) выбрать наиболее эффективные формы проведения интегрированных занятий;
5) выбрать формы контроля достижения поставленных целей [2].
Рассмотрим пример интегрированного семинара. В качестве ведущей дисциплины, выступающей интегратором, возьмем теорию вероятностей и математическую статистику. Вспомогательной дисциплиной, способствующей углублению, расширению, уточнению материала ведущей дисциплины будет служить экономика.
Актуальность. Математика занимается изучением математических моделей реальных явлений. Явления окружающего нас мира можно условно разделить на закономерные (причинно-следственные) и случайные. Человек в процессе познания окружающего мира анализирует данные явления, используя при этом закономерности двух типов – динамические (они позволяют делать однозначные предсказания) и статистические (они позволяют делать вероятностные предсказания). Эволюция научной картины мира, связанная с постепенно углубляющимся процессом научного познания человеком окружающего его мира, убедительно продемонстрировала фундаментальность вероятностных (статистических) закономерностей, которые стали сегодня основой научного миропонимания. Наука XX столетия доказала, что именно статистические (а не динамические) закономерности более адекватно отражают реалии нашего мира [4].
Теория вероятностей – это раздел математики, направленный на изучение случайных, не подлежащих строгому математическому описанию, событий и явлений, их свойств, закономерностей и взаимосвязей.
Очевидна взаимосвязь теории вероятностей и экономики. Ведь характер любой экономической деятельности не является строго детерминированным. Это означает, что осуществляя ту или иную экономическую операцию, заключая ту или иную сделку, анализируя динамику макроэкономических показателей и т.д., нельзя точно предсказать конечный результат, поскольку по своей природе все такие операции и показатели случайны.
Тема семинара: «Применение теории вероятностей в экономике».
Тип занятия: интегрированный семинар обобщения и систематизации знаний, умений и навыков.
Форма обучения: групповая (по 3-5 человек).
Цели семинара:
● систематизировать и обобщить выделенные ранее знания о распределениях дискретной случайной величины;
● показать связь теории вероятностей с экономикой.
В результате студент:
● знает виды распределения дискретной случайной величины;
● умеет решать задачи на распределение дискретной случайной величины;
● осознает связь теории вероятностей с экономикой;
● ориентируется в основных проблемах экономики и финансов, при решении которых полезно применение вероятностно-статистических методов;
● умеет по экономической постановке задачи определить в каком разделе математики искать средства для ее решения;
● умеет переходить от экономической постановки задачи к ее математической модели, проводить по этой модели расчеты и получать числовые результаты, анализировать эти результаты и делать количественные и качественные выводы, необходимые для принятия решений в данной области.
Таблица 1
Задача
|
Условия |
Вопросы к задаче |
|
Фермер предполагает, что через месяц, когда он соберет урожай, цена пшеницы в каждом из восьми регионов, куда он обычно ее продает, может с вероятностью 0,8 понизиться и с вероятностью 0,2 повыситься, поэтому он заключает с восемью мельниками в этих регионах восемь форвардов на поставку им пшеницы через месяц по сегодняшней цене. Цены в регионах изменяются независимо [7]. |
1) В чем состоит финансовая операция форвард? 2) Назовите отличительные черты форвардных контрактов. 3) Что такое форвардная цена актива? 4) Перечислите виды форвардных контрактов. 5) Найдите математическое ожидание числа форвардов, которые окажутся выгодными для фермера и вероятность того, что все восемь форвардов окажутся для него выгодными. 6) Интерпретируйте экономический смысл полученных результатов. 7) Заполните соответствующую строчку в табл. 2. |
Таблица 2
Основные законы распределения дискретных случайных величин
|
Название |
Условия возникновения |
Формула |
Числовые характеристики |
|
|
Биномиальный
|
Проводится ряд одинаковых независимых испытаний. Х – число успехов в n испытаниях Бернулли с вероятностью p успеха в единичном испытании. |
|
M(X) = np D(X) = np (1 –p) |
|
|
Геометрический
|
Проводится ряд одинаковых независимых испытаний до первого появления некоторого события А. Х – число испытаний Бернулли, которые придется произвести до первого успеха. |
|
|
|
|
Пуассона |
|
Х число успехов в n испытаниях Бернулли с вероятностью p успеха в единичном испытании, когда n велико (несколько десятков или более), а |
|
|
|
|
Х число наступлений события простейшего потока с интенсивностью μ за время t. |
|
|
|
Инвариантная структура любого современного урока математики включает в себя три основные части:
Мотивационно-ориентировочная часть (10 мин)
На этом этапе проводится актуализация знаний. Рассмотрим вопросы, которые можно предложить студентам на этом этапе работы.
1. Математика занимается изучением математических моделей реальных явлений. На какие два вида можно условно разделить явления окружающего нас мира?
2. Какие явления называются закономерными? Приведите примеры закономерных явлений.
3. Какие явления называются случайными?
4. Что изучает теория вероятностей? Какая связь между теорией вероятностей и экономикой?
5. Сформулируйте определение случайной величины. Приведите примеры случайных величин в экономике.
6. Какие вы знаете виды случайных величин?
7. Какие вы знаете виды распределения дискретной случайной величины?
Данный этап завершается объявлением темы занятия.
Операционно-познавательная часть (50 мин)
На этом этапе каждая группа получает одну ситуационную задачу по одному виду распределения дискретной случайной величины. Работая в группах по 3-5 человек, студенты:
1) составляют математическую модель для решения задачи;
2) решают задачу;
3) формулируют определения экономических понятий приведенных в задаче;
4) интерпретируют экономический смысл полученных результатов;
5) заполняют соответствующую строчку в табл. 1 для своего вида распределения.
Далее, представители из каждой группы рассказывают решение своей задачи [1].
Рассмотрим пример задачи, которую можно предложить студентам на этом этапе работы.
Рефлексивно-оценочная часть (30 мин)
Рефлексивно-оценочная часть учебной деятельности должна быть направлена на формирование регулятивных универсальных учебных действий, обеспечивающих становление и развитие действий самоанализа, самоконтроля и самооценки в процессе обучения математике [6]. На этом этапе организуется осознание, осмысление деятельности и ее результатов.
Студенты, систематизируя и обобщая выделенные ранее знания о распределениях случайной величины, совместно с преподавателем проверяют табл. 1, которая была заполнена ими в группах на предыдущем этапе.
Выводы
Установление междисциплинарных связей в образовательной практике высшего образования ведет к качественному развитию общих и профессиональных компетенций. Теория вероятностей и математическая статистика как наука и как учебная дисциплина обладает значительным потенциалом для установления междисциплинарных связей. Приведенный материал можно использовать в процессе обучения теории вероятностей и математической статистике студентов экономических специальностей. Анализируя решения приведенных задач студенты не только закрепляют и углубляют полученные теоретические знания, но и учатся применять эти знания при постановке и решении реальных экономических задач.


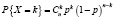
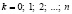 .
.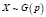
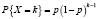
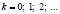
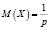
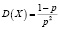
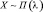
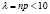 .
.