В процессе проведения финансового анализа инновационных проектов, в процессе принятия управленческих решений учитывают прогноз инфляции [2]. Показатель инфляции есть индикатор стабильности. Концепция учета влияния фактора инфляции в бизнес – планировании инновационного проекта заключается в необходимости реального отражения стоимости активов и денежных потоков, в обеспечении возмещения потерь доходов, вызываемых инфляционными процессами. Инфляция искажает результаты финансового анализа. Например, оценка основных средств не может учитывать реальный рост стоимости основных средств, так как базируется на первоначальной стоимости. Темп инфляции влияет на изменение сроков оборачиваемости активов. В результате происходит завышение финансовых результатов деятельности, которое сказывается на увеличении срока окупаемости проекта.
В связи с этим возникает необходимость в прогнозировании инфляции, в формировании методологии прогнозирования [3].
Анализ моделей, которые используют для прогнозирования инфляции в России, показал, что чаще всего на практике используют кривую Филлипса в рамках комплексной модели, которая описывает экономику в целом.
Прогнозирование российской инфляции с помощью модели временных рядов и при помощи факторных моделей имеет ряд преимуществ [1]:
– простота;
– гибкость;
– единообразие проектирования;
– прозрачность моделирования.
Таким образом, целью исследования стало построение трендовой модели прогнозирования показателя инфляции на 2016-2018 гг.
Цель исследования определила задачи исследования:
– на основе статистических данных годового показателя инфляции в России построить модель;
– построенную модель проверить на адекватность;
– проверить модель на точность с целью ее использования как модели прогнозирования;
– определить доверительный интервал прогноза.
В основу построения модели прогнозирования годовой инфляции в России на 2016, 2017, 2018 года положен временной ряд годовой инфляции с 2000 года по 2015 год (табл. 1).
Таблица 1
Уровень инфляции в России по годам в %
|
t |
1 2000 |
2 2001 |
3 2002 |
4 2003 |
5 2004 |
6 2005 |
7 2006 |
8 2007 |
9 2008 |
10 2009 |
11 2010 |
12 2011 |
13 2012 |
14 2013 |
15 2014 |
16 2015 |
|
yt |
20,1 |
18,8 |
15,06 |
11,99 |
11,74 |
10,91 |
9,00 |
11,87 |
13,28 |
8,80 |
8,78 |
6,10 |
6,58 |
6,45 |
11,36 |
12,91 |
Анализ временных рядов начинают с выявления и устранения аномальных значений уровней ряда, с определения наличия тренда в исходном временном ряде. Для выявления аномальных уровней временных рядов, используют методы, рассчитанные для статистических совокупностей [1]. В работе использовался метод Ирвина:
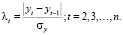
Расчетные значения λ2, λ3,…,λn сравнивали с табличными значениями критерия Ирвина λα и сделали вывод об отсутствии во временном ряде аномальных уровней.
Наличие тренда во временном ряду определяли методом проверки разности средних. Исходный временной ряд разбивали на две равные по числу уровней части. Для каждой из двух частей определяли средние значения и дисперсии:
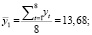
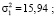
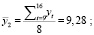
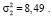
Равенство дисперсий обеих частей ряда проверяли с помощью критерия Фишера. Расчетное значение критерия Фишера:
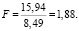
Табличное значение критерия Фишера при уровне значимости α = 0,05:
F = 3,79.
Полученные расчеты дали возможность принять гипотезу о равенстве дисперсий, т.е. о существующей закономерности в изменении значений исследуемого временного ряда. Гипотезу об отсутствии тренда в исходном временном ряду при уровне значимости α = 0,05 проверяли с помощью критерия Стьюдента. Сравнение расчетного значения критерия Стьюдента и табличного значения критерия позволило принять альтернативную гипотезу о наличии тренда.
Структуру временного ряда определяли, рассчитав несколько последовательных коэффициентов автокорреляции и выявив лаг, для которого значение выборочного коэффициента автокорреляции наибольшее. Для обеспечения статистической достоверности коэффициентов автокорреляции использовали правило: максимальный лаг должен быть не больше, чем n/4. Для исследуемого временного ряда максимальный лаг τ = 4.
В процессе вычислений получена автокорреляционная функция временного ряда (табл. 2).
Таблица 2
Автокорреляционная функция
|
Лаг |
1 |
2 |
3 |
4 |
|
Коэффициент автокорреляции уровней |
0,538 |
0,338 |
0,103 |
-0,075 |
Анализ значений автокорреляционной функции позволил сделать вывод о наличие во временном ряду только тенденции и отсутствии циклических колебаний [1].
Следующим шагом проводили моделирование тенденции временного ряда. Один из способов моделирования временного ряда – это аналитическое выравнивание временного ряда. С целью определения вида функции рассчитывали абсолютные приросты уровней ряда, определяли относительную скорость изменения годовой инфляции через коэффициент роста, определяли относительную скорость изменения годовой инфляции через коэффициент прироста. Проведенные расчеты позволили сделать предположение, что выравнивание временного ряда возможно либо по показательной функции:
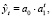
либо по полиному четвертой степени:
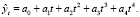
Метод наименьших квадратов позволил определить параметры уравнений:
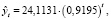
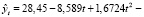
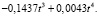
Следующий этап – это установление адекватности одной из полученных трендовых моделей. Трендовая модель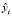 
адекватна в том случае, если она правильно отражает систематические компоненты временного ряда, т.е. остаточная компонента 
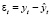(t = 1,2,…,n) должна удовлетворять следующим свойствам [3]:
– случайность колебаний уровней остаточной последовательности;
– соответствие распределения случайной компоненты нормальному закону распределения;
– равенство математического ожидания случайной компоненты нулю;
– независимость значений уровней случайной компоненты.
Для исследования случайности отклонений от тренда используют непараметрические критерии. В исследование использовали критерий пиков. Критерием случайности на 5 %-ом уровне значимости считают выполнение неравенство:
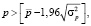
где математическое ожидание числа поворотных точек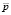 
и дисперсию 
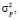рассчитывают по формулам:
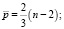
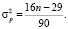
Выполнение неравенства для полинома четвертой степени позволило сделать вывод о том, что свойство случайности ряда остатков подтверждается. Данный факт указывает на адекватность построенной модели.
Проверку соответствия остаточной последовательности нормальному закону распределения проводили с помощью RS – критерия [1]. Критерий численно равен отношению размаха вариации случайной величины (R) к стандартному отклонению S:
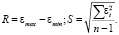
Расчетное значение RS – критерия сравнивали с табличными значениями RS – критерия на 5 %-ом уровне значимости при n = 16: 3,01 и 4,24. Расчетное значение критерия для полинома четвертой степени попало в интервал между нижней и верхней границами табличных значений, что позволило сделать вывод: свойство нормальности распределения последовательности εt выполняется.
Следующим шагом проверяли равенство математического ожидания случайной компоненты нулю на основе критерия Стьюдента. Расчетное значение критерия Стьюдента и табличное значение критерия на 5 % уровне значимости указали на возможность принятия гипотезы о равенстве нулю математического ожидания случайной последовательности εt
Следующим шагом проверяли независимость значений уровней случайной компоненты, т.е. отсутствие существенной автокорреляции в остаточной последовательности модели в виде полинома четвертой степени по критерию Дарбина – Уотсона:
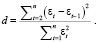
Сравнение расчетного и табличного значений позволило принять гипотезу о независимости уровней остаточной последовательности.
Проведенное исследование подтвердило адекватность трендовой модели:
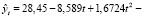
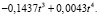
Следующий этап исследования – это оценка точности адекватной трендовой модели.
В качестве статистического показателя точности была принята средняя относительная ошибка аппроксимации:
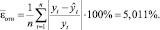
Полученная ошибка свидетельствует об удовлетворительном уровне точности трендовой модели.
Интервальный прогноз осуществляли путем расчета доверительного интервала, т.е. интервала, в котором с определенной вероятностью ожидают появление прогнозируемого показателя:
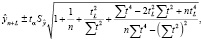
где L – период упреждения,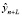 
– точечный прогноз по модели,
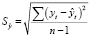
– стандартная ошибка оценки прогнозируемого показателя, tα – табличное значение критерия Стьюдента для уровня значимости 5 % и числа степеней свободы n-2.
Прогнозное значение показателя инфляции на 2016 год – 18,9 %.
Заключение
В результате проведенного исследования была построена трендовая модель прогнозирования годового показателя инфляции:
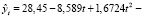
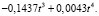
Полученная модель проверена на адекватность и точность.
Для прогнозного показателя годовой инфляции определен доверительный интервал:
18,9 ± 4,099.
Аналогично рассчитывают прогнозное значение показателя инфляции на 2017, 2018 и 2019 годы.