Грунты являются самыми распространенными строительными материалами. Из них строят плотины, земляное полотно железных и автомобильных дорог. Они являются преимущественно основанием для строящихся любых гражданских и крупнопромышленных сооружений.
По своему составу и свойствам грунты не могут быть отнесены ни к твердым, ни к жидким, ни тем более к газообразным веществам. Он представляет собой сложную комбинацию ряда веществ с резко различными свойствами. Даже в твердой фазе грунт по своим свойствам резко отличается от любых твердых тел. Они сложены из бесчисленного количества отдельных частиц. Отсюда и возникает то обязательство, что прочность и условия работы грунтов зависят от совокупного действия этих частиц и одновременно от взаимодействия в грунте его фаз: твердой, жидкой и газообразной.
Свойства грунтов и их природа, вообще говоря, изменяются в очень широких пределах [6]. Поэтому человек, сталкивающийся в своей практике с тем или иным грунтом, должен иметь более ясное представление о грунтах, обоснованных на их свойствах. Даже небольшая неправильная оценка этих свойств могут привести к тем или иным ошибкам.
Возведение сооружений и выполнение всякого рода земляных работ связано с природным залеганием грунтов. При этом любой строитель сталкивается с условиями работы грунтов в их естественном природном состоянии, когда они служат основанием для сооружений и он в ответе за правильное решение всех вопросов, для этого он и должен обладать необычайно широкой научной подготовкой и опытом.
Уплотнение (консолидация) грунта в основном определяется своей сжимаемостью. Сжимаемость основания зависит как от типа грунта, так и от характера нагрузки. Длительно действующие нагрузки наоборот сильно уплотняют глинистые грунты. Явление сжимаемости грунтов имеет весьма большое значение при проектировании инженерных сооружений на консолидируемом основании. При этом деформация сжатия грунтов в основном происходит вследствие сближения твердых частиц между собой и оценивается изменением коэффициента пористости при изменении сжимающих напряжений в скелете грунта σ. Определение зависимости между коэффициентом пористости и сжимающими напряжениями в скелете грунта обычно производится лабораторным путем в компрессионных приборах.
Если стареющая однородная грунтовая среда обладает свойством линейной ползучести, то зависимость между коэффициентом пористости и суммой главных напряжений имеет вид
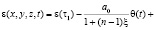
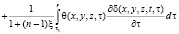, (1)
где
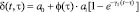; (2)
ε(t), θ(t) – эти функции также изменяются по координатам x, y, z; Φ(τ) – функция старения; a1, γ1 – параметры ползучести; t1 – момент приложения внешней нагрузки; ξ – коэффициент бокового давления; а0 – коэффициент сжимаемости грунта, который в общем виде может зависеть от глубины исследуемой точки и времени; п – размерность рассматриваемой задачи.
Зависимость (1) при n = 1 и (2) для одномерной задачи теории уплотнения однородных грунтов впервые была применена В.А. Флориным [4]. Он теорию упругоползучего тела Г.Н. Маслова-Н.Х. Арутюняна [1] смог применить к описанию процесса уплотнения глинистых грунтов, обладающих свойством ползучести. Экспериментальные исследования С.Р. Месчяна [5] доказали применимость этой теории к водонасыщенным глинистым грунтам.
Функция старения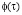 
, в (2), обычно представляется в виде [2, 1].
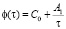. (3)
Здесь С0, А1 – опытные данные, τ – время приложения нагрузки.
Чтобы решить те или иные задачи механики уплотняемых пористых трехфазных грунтовых сред необходимо совместно рассматривать выражение (1) с уравнением, отражающим условие неразрывности жидкой и твердой фаз грунта
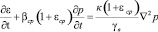(4)
и условием равновесия уплотняемого грунтового массива
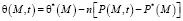. (5)
Здесь εcp – среднее значение коэффициента пористости в процессе уплотнения; γв – объемный вес воды; t – время уплотнения грунтового массива; ∇2 – оператор Лапласа; p(M, t) – давление в поровой жидкости; βcp – коэффициент объемного сжатия; к – коэффициент фильтрации; М(x, y ,z) – исследуемая точка уплотняемого массива; x, y, z – координаты точки в пространстве; θ*(М) – сумма главных напряжений для стабилизированного состояния грунта; р*(М) – поровое давление для этого же состояния.
Исследовав совместно выражения (1)-(5), уравнение одномерной задачи консолидации грунтов в безразмерных координатах приводим к виду:
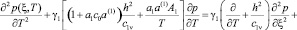
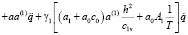, (6)
где
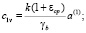
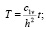
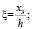
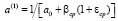. (7)
Начальными условиями для данной задачи будут:
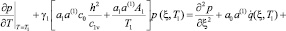
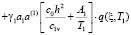; (8)
(9)
Для двумерной задачи уравнения (6)-(9) имеет вид:
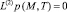. (10)
L(2) – дифференциальный оператор вида:
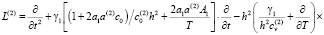
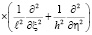, (11)
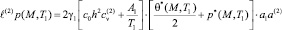, (12)
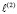– оператор вида
,
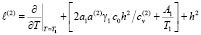
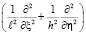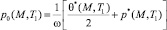(13)
где x,h – безразмерные координаты;
с0 – предельное значение меры ползучести для уплотняемого грунта;
А1 – параметр, зависящий от свойств и условий старения грунта;
a0, βcp, ξ, к, γb, εcp имеют те же значения, что и в предыдущих подразделах.
Для трехмерной задачи уравнения (6)-(9) имеет вид:
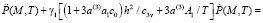
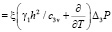(14)
начальным
+
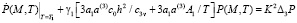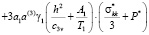(15)
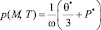. (16)
Таким образом, имеем, что уравнения механики уплотняемых земляных масс связывают временное и пространственное распределение давлений в поровой жидкости внутри исследуемого грунтового массива в любой момент времени t > τ1. Чтобы найти его необходимо знать закон распределения давлений внутри уплотняемого массива в начальный момент времени, геометрическую форму и размеры уплотняемого грунтового массива, и закон фильтрующей поверхности тела между окружающей средой с определенными граничными условиями.
Вначале рассмотрим решение одномерной задачи консолидации наследственно-стареющих грунтов. Для этого решим уравнение (6). В качестве расчетной схемы примем так, чтобы слой грунта мощностью h в момент времени t = τ1 подвержен действию внешней распределенной нагрузки с интенсивностью q = q(x3, t). Верхняя поверхность уплотняемого массива водопроницаема, а нижняя водонепроницаемая. Тогда граничные условия применительно данной задаче запишутся так:
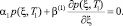(17)
Причем согласно условию задачи, при ξ = 0 имеет место β(1) = 0 и при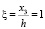 
, α(1) = 0.
Заметим, что уравнение (6) для однородного грунта при q3(x3, t) = const исследовано в [4].
Итак в безразмерных координатах требуется определить давление в поровой жидкости p(ξ, T), напряжение в скелете σ(ξ, T) и вертикальные перемещения верхней поверхности S(T) (осадок) грунтового слоя в области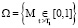 
, если p(ξ, T) удовлетворяет дифференциальному уравнению (6) начальным (8), (9) и граничным (17) условиям при (7).
Решение уравнения (6), удовлетворяющее указанным условиям, представим в виде
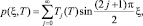
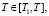
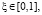(18)
где
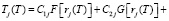
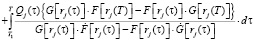. (19)
,
.
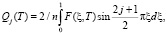
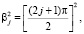
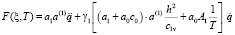
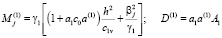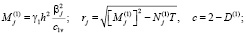
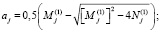
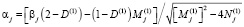Здесь F(αj, c, rj) и G(αj, c, rj) соответственно являются вырожденными гипергеометрическими функциями первого и второго родов. При этом F(αj, c, rj) называется функцией Куммера. Она разлагается в степенной ряд
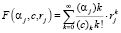. (20)
Тогда функция G(αj, c, rj) через F(αj, c, rj) выражается следующим образом:
.
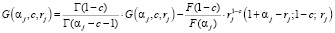Причем ряд (20) сходится при всех rj.
Таким образом, распределение порового давления в уплотняемом упругоползучем грунтовом стареющем массиве мощности h происходит по формуле (18). При этом функция Tj, входящая в эту формулу, находится из (19).
Для вычисления осадок S(T) грунта в безразмерной координате используем формулу вида
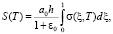(21)
где σ(ξ, T) – напряжение в скелете грунта. Оно находится из
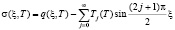. (22)
Подставив выражение (22) в (21), находим
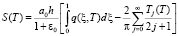. (23)
При Т → 0 имеем, что σ(ξ, T) → 0, а при Т → ∞ напряжение стремится к q.
Следовательно, если поровое давление изменится от q до 0, то напряжение принимает значение от 0 до q. При этом S(T) изменится от 0 до
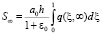. (24)
Если q(ξ, T) =q = const то из (48) находим, что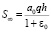 
, т.е. неустановившаяся осадка слоя уплотняемого грунта во времени изменяется в диапазонах от 0 до 
.
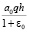Теперь рассмотрим решение двумерной задачи консолидации наследственно-стареющих грунтов. Для этого исследуем уплотнение грунта с водоупором на глубине h, ограниченном с боков водонепроницаемыми стенками, и находящимся под действием равномерно распределенной нагрузки q, приложенной на участке (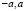
) поверхности массива. Для данной задачи граничными условиями будут:
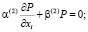
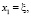
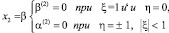(25)
Тогда применительно к данной схеме задачу можно сформулировать следующим образом: требуется определить непрерывную функцию р(M, t), удовлетворяющую в области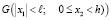 
уравнению (10), начальным (12), (13) и граничным (25) условиям.
Здесь следует заметить, что данная задача для начального момента времени исследована в [5]. Выражение (13) в безразмерных координатах, определяющее начальное распределение порового давления для трехфазной среды имеет вид:
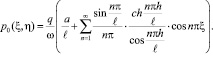(26)
Решение исследуемой краевой задачи (12), (13), (25) получим в виде
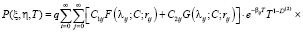
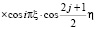, (27)
где
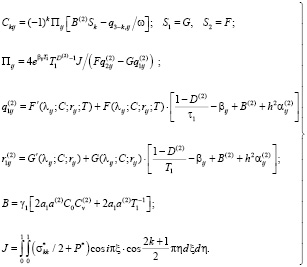
Используя соотношение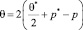 
сумму главных напряжений представим в виде
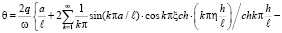
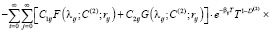
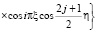, (28)
Тогда осадку уплотняемого слоя грунта определим по формуле
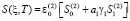, (29)
где
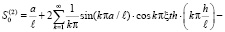
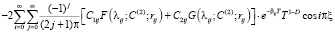(79)
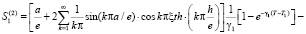
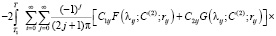
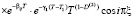. (30)
Таким образом, задача консолидации трехфазного грунта с учетом линейной ползучести и старения скелета можно сказать полностью решена для равномерно распределенной уплотняющей нагрузки.
В полученных решениях скорость консолидации зависит от безразмерных параметров A(2), B(2, a(2), T, которые в свою очередь зависят от параметров a0, a1, c0, t, определяемые по результатам компрессионных испытаний грунтов, которые для различных глинистых пород в основном имеются.
Анализ полученных формул дает, что развитие порового давления во времени имеет экстремальный характер, а осадка по времени после полного рассеивания порового давления продолжается пропорционально логарифму времени.
Далее рассмотрим решение трехмерной задачи консолидации наследственно-стареющих грунтов применительно к уплотнению грунтового массива в виде параллелепипеда с водоупором на глубине h и с водонепроницаемыми стенками на 2l1 и 2l2, находящегося под действием равномерно распределенной нагрузки с интенсивностью q, приложенной на части поверхности этого параллелепипеда со сторонами 2a и 2b.
По условию задачи граничными условиями при t = τ1 будут:
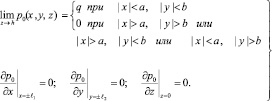(32)
Чтобы определить распространение мгновенных давлений в поровой жидкости, в указанном слое грунта, необходимо решить дифференциальное уравнение вида
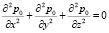. (33)
Здесь функция p0(x, y, z) зависит от пространственных координат. Это уравнение при граничных условиях (32) исследовано в [4].
Его решение для трехфазной земляной массы относительно безразмерных координат имеет вид:
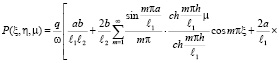
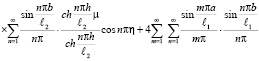
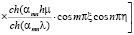. (34)
Граничные условия данной задачи в безразмерных координатах можно представить следующим образом:
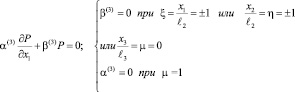(35)
Итак, для решения исследуемой задачи требуется найти непрерывную функцию, отражающую изменение давлений в поровой жидкости и удовлетворяющую в области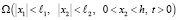 
дифференциальному уравнению вида (14), начальным (15),(16) и граничным (31) условиям.
Решение уравнения (14), удовлетворяющее граничным условиям (31), получим в виде:
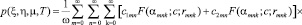
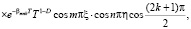(36)
где
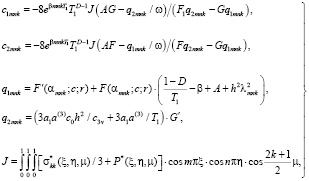(37)
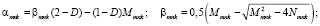
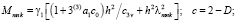
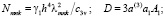
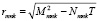
После определения давления в поровой жидкости осадку уплотняемого слоя грунта можно вычислить по формуле:
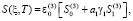(38)
где
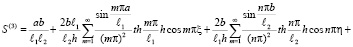
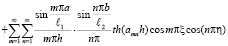, (39)
,
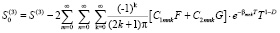
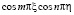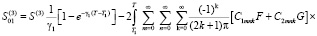
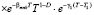
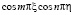dT. (40)
Таким образом, пространственная задача консолидации многофазного грунта с учетом его линейной ползучести и старения скелета, можно сказать решена полностью. Выражения (36) и (38) при (37), (39),(40) дают возможность установить закон изменения порового давления и осадку уплотняемого массива во времени и пространственных координатах. Причем в эти решения, полученные в замкнутом виде, входят различные параметры грунта.
Анализ полученных решении показал, что учет старения скелета приводит к новым результатам, как по качеству, так и по количеству.
1 Получено решение одномерной задачи консолидации многокомпонентных упругоползучих грунтов с учетом их старения. При этом анализ полученных данных показал, что с увеличением мощности уплотняемого грунтового массива максимальное значение порового давления и время его наступления увеличивается, а значение осадки уменьшается в течение всего периода уплотнения. Это означает, что с увеличением толщины уплотняемого слоя грунта уменьшается скорость нарастания напряжений в скелете грунта. Следовательно, чем больше мощность уплотняемого грунтового массива, тем медленнее протекают фильтрационные процессы. Другими словами, процесс возрастания порового давления будет продолжаться за счет ползучести и старения скелета грунта. На величину порового давления влияет также и темп нарастания внешней нагрузки.
2 Установлено, что одновременный учет влияния старения и ползучести скелета возрастает, явление выжимания воды той или иной интенсивности могут возникать при любой плотности грунта, если внешняя нагрузка или напряжения в скелете грунта достаточно велики. Уменьшение порового давления во времени после достижения максимума в супесях происходит быстрее, чем в глинах. В целом, анализ численных результатов показал, что продолжительность процесса уплотнения глинистого грунта почти не зависит от скорости фильтрации. Этот фактор видимо объясняется тем, что если проницаемость грунта очень велика, то определяется его вязким сопротивлением.
Одновременный учет старения и ползучести скелета грунта снижает величину порового давления в процессе консолидации, увеличивает величину начальной осадки и замедляет скорость протекания осадки по сравнению с фильтрационной теорией уплотнения земляных масс.
3. Получены решения двумерной задачи. В этих решениях скорость консолидации зависит от безразмерных параметров, которые в свою очередь зависят от параметров, определяемых по результатам компрессионных испытаний грунтов. Численный анализ показал, что развитие порового давления во времени имеет экстремальный характер, а осадка по времени после полного рассеивания порового давления продолжается пропорционально логарифму времени.
4. Получены аналитические решения трехмерной задачи консолидации упругоползучих неоднородных грунтов. Все решения представлены в виде расчетных формул, которые дают возможность определить давление в поровой жидкости, напряжения в скелете грунта и вертикальные перемещения точек верхней поверхности уплотняемого массива.
Следует заметить, что на основе выражений (36) – (40) можно также получить решения задач для других случаев нагружения уплотняемого грунта. В частности, для сосредоточенной силы. Многомерные задачи консолидации многофазных грунтов также исследованы в [2, 3].