Несмотря на разрешение многих принципиальных вопросов, в настоящее время в литературе отсутствует полное решение ряда задач, появляющихся при исследовании и совершенствовании подвеса ротора в регулируемом электростатическом поле, связанных с влиянием температуры окружающей среды на стабильность угловой скорости, а также анализ уводящих моментов, возникающих вследствие упругих деформаций чувствительных элементов навигационных систем.
На стабильность угловой скорости влияет изменение размеров ротора, происходящее при изменении температуры окружающей среды. Возникновение градиентов температуры внутри ротора приведет к неодинаковому расширению материала ротора ЭСГ и будет сопровождаться изменением его напряженно-деформированного состояния, что в свою очередь приведет к изменению внешней поверхности ротора.
Источники возмущающих моментов, приложенных к ротору ЭСГ, могут быть вызваны следующими причинами [1]:
– погрешностями формы ротора и электродов подвеса;
– наличием магнитных полей в пространстве, окружающем ротор;
– неоднородностью гравитационного поля;
– наличием остаточного газа в зазоре между электродами подвеса и ротором.
Причинами возникновения не сферичности ротора является погрешности изготовления ротора, центробежные силы, возникающие при его вращении, термоупругие деформации, появляющиеся при изменении температуры.
Рассмотрим твердое тело, подвешенное в вакууме в некотором силовом поле. Подвес шарового ротора осуществляется в вакууме в регулируемом электрическое поле. Поддерживающие силы в таком подвесе можно считать направленными по нормали к поверхности ротора, у которого центр масс совпадает с геометрическим центром, момент поддерживающих сил относительно центра масс оказывается равным нулю. При этом ось вращения гироскопа будет неограниченно долго сохранять неизменное направление в пространстве. В действительности поверхность ротора всегда отличается от сферической, поэтому в реальном приборе возникает возмущающий момент, величина которого и определяет точность прибора [1].
Для расчета главного вектора и главного момента сил, действующих на ротор, используются формулы [1]
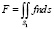(1)
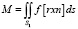(2)
Здесь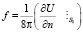 
– плотность поддерживающих сил, действующих на элемент поверхности ds; n – единичный вектор внешней нормали к поверхности ротора S1 : r – радиус вектор, проведенной из центра масс в точку поверхности ротора S1 : U – функция потенциала пола в электростатическом подвесе. В работе [2] проводится расчет поля в подвесе электростатического гироскопа, и при достаточно малых зазорах между электродами подвеса и ротора, получено выражение для плотности поддерживающих сил
, 
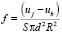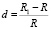(3)
где uj потенциал j-го электрода, ub-потенциал ротора, R1 – радиус сферы, на которой расположены электроды, d – относительный зазор между ротором и электродами.
Потенциал ротора определяется формулой [1]
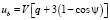(4)
Здесь q – заряд ротора.
Проекции главного момента на оси трехгранника 123 для сферической системы 11 с полярной осью 3, имеют вид [2, 3]
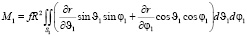
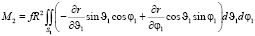
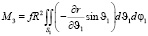(5)
Для определенности рассмотрим шести электродный подвес ротора. Пронумеруем электроды таким образом, чтобы положительному направлению оси i соответствовал (2i-1) – й электрод, а отрицательному (2i)-й электрод. Согласно [2] уравнения поверхностей электродов S имеют вид
, 
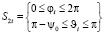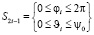(6)
Полагая в [4, 11]
,
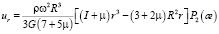
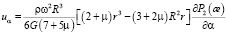
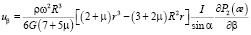Где
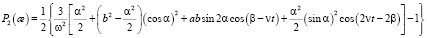
первое уравнение r = 1, получим уравнение деформации ротора в сферических координатах трехгранника, жестко связанного с ротором
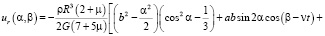
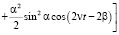(7)
Для проведения асферизации ротора вращаем его вокруг оси динамической симметрии 0x3. При этом угол нутации = 0, откуда следует, что проекции вектора угловой скорости на ось x1 a = 0, на ось x3 = L/IЗ. Поставляя эту проекцию угловой скорости в (7), получим уравнения деформации ротора при вращении его вокруг 0x3
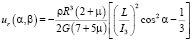
Затем, вычитая последнее из (7), можно написать уравнение поверхности деформированного ротора в движении, близком к движению Эйлера-Пуансо, с учетом его деформации.
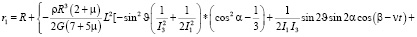
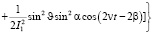(8)
Принимаем во внимание (2.3) и (2.6), перепишем уравнение (8) в сферическими координатами , и 1, 1 с полярной осью 3 определяется следующим образом
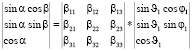(9)
Предположим, что вектор кинетического момента лежит в плоскости 13, т.е. = 0, учитывая (2.6), получим следующие выражения
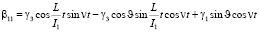
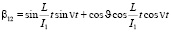
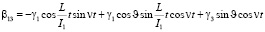
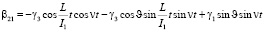
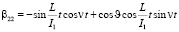(10)
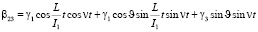
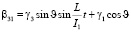
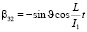
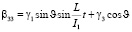
С учетом (9) получим уравнение деформированной поверхности ротора в трехграннике 123, жестко связанном с корпусом ротора в сферических координатах 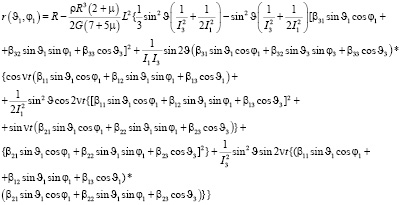1, 1
(11)
Подставляя уравнение (11) в формулы (5) и выполняя интегрирование по поверхностям электродов (6), затем осредняя полученные выражения по явно выходящему времени, с учетом (10) имеем для проекции момента поддерживающих сил, действующих со стороны пятого и шестого электродов, следующие выражения, соответственно
, 
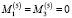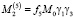(12)
, 
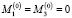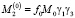
где
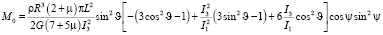
В рассматриваемой сферической системе координат интегрирование (6) по поверхностям других электродов затруднительно, однако, учитывая симметрию данной конфигурации электродов подвеса, требуемый результат можно получить при использовании других сферических координат с полярным осями 2 и 3 при интегрировании S3 и S4 и соответственно – по S1 и S2. Выполнив указанные преразования, находим
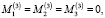
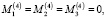(13)
, 
, 
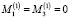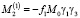
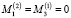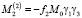
Используя (12) и (13), находим выражения для проекций суммарного момента, действующего на ротор со стороны всех электродов
,
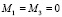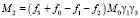(14)
В общем случае, когда кинетический момент расположен произвольным образом относительно системы координат 123, проводя аналогичные рассуждения как и в случае, когда вектор кинетического момента лежит в плоскости 13, имеем для проекций момента поддерживающих сил, действующих со стороны всех электродов подвеса следующие выражения
,
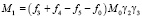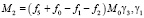(15)
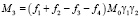
Введем в рассмотрение функцию
W = W(1, 2, 3) (16)
Производные по углам 1, 2, 3 от функции (16) дают проекции моментов сил, действующих по нормали к поверхности ротора на оси неподвижного трехгранника 123 [1]:
,
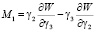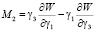(17)
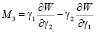
Из (15), (16) и (17) видно, что в рассматриваемом случае силовая функция моментов сил является квадратичной формой направляющих косинусов вектора кинетического момента ротора
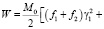
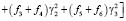(18)
В случае, когда твердое тело неподвижно в неконтактном подвесе, главный вектор поддерживающих сил F уравновешивается главным вектором массовых сил, приложенных к телу (массовыми силами являются сила тяготения, сила инерции переносного движения и т.д.). Таким образом, силовая функция (18) представляет собой силовую функцию маятника, у которого масса равна массе тела, а центр масс смещен из центра неконтактного подвеса на величину R11. При этом возмущения, определяемые силовой функцией (18), будут линейными. (Возмущения называются линейными, если для них можно построить силовую функцию, линейно зависящую от направляющих косинусов осп симметрии тела с неизменно ориентированными в пространстве осями 123.
Принимая во внимание формулы для плотности поддерживающих сил (3), перепишем силовую функцию в виде
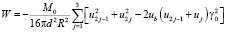(19)
Для последующего анализа моментов необходимо конкретизировать выражения для потенциалов uj.
Электроды, отвечающие разным каналам системы регулирования подвеса, не должны пересекаться, поэтому величина 0 = cos0 в (12) удовлетворяет неравенству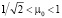 
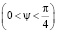. Следовательно, начиная с пятой гармоники, можно выбрать такой угол 0, определяющий размер электрода, чтобы
Pk –1(cos0) – Pk +1(cos0) = 0
При указанном выборе 0 момент, обусловленный наличием k-й гармоники в форме тела, будет тождественно равен нулю. В частности, при k = 5 корень вышеуказанного уравнения 40, 34 ° при k = 6, 29 ° при k = 7 и т.д.
Остановимся на рассмотрении системы регулирования на постоянном токе. В этом случае потенциалы электродов uj удовлетворяют неравенству [1]:
0 uj 2V0
Здесь V0 – «опорное» напряжение на электродах. Если пренебречь динамикой системы регулирования, то закон управления потенциалами электродов можно записать
u2j –1 = V0 – Vj, u2j = V0 + Vj,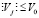 
(20)
где Vj = const – добавочное напряжение, подаваемое системой регулирования на электроды для обеспечения стабилизации положения центра масс ротора на оси подвеса.
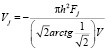
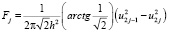
Согласно [1] при линейном законе регулирования потенциалов электродов (20) величину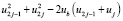 
в (2.81) можно выразить через проекцию на ось 2 главного вектора поддерживающих сил, приложенных к телу
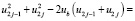
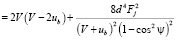(21)
Представим проекции равнодействующей поддерживающих сил F на оси 1, 2 и 3 в виде
F1 = F sin 1 cos 1,
F2 = F sin 1 sin 1, F3 = cos 1
Здесь два угла 1 и 1 сферической системы координат с полярной осью 3, характеризует положение главного вектора массовых сил.
Потенциалы электродов не могут быть произвольными: установившимся режиме работы электростатического гироскопа на неподвижном основании главный вектор поддерживающих сил F уравновешивается силой тяжести ротора Р.
Подставляя (19) с учетом (21), (4) и проекции вектора поддерживающих сил (17) получим квадрат модуля моментов сил, действующих на незаряженный ротор со стороны электростатического поля
,
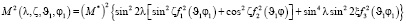где
, 
,
,
.
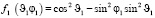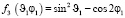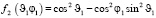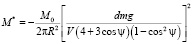Исследуем зависимость возмущающего момента от ориентации вектора кинетического момента. Видно, что в случае, когда = 0, т.е., когда вектор кинетического момента направлен по оси 3 момент равен нулю.
Максимального значения момент достигает в случае, когда сила тяжести коллинеарна одной из осей симметрии электродов, т.е. когда в (18) F1 = mg [1, стр. 108.].
Числовой пример. Рассмотрим электростатический гироскоп, у которого физические и геометрические характеристики: радиус ротора R = 0.5 см, механические характеристики: плотность = 1850 кг/м3, модуль сдвига G = 1,15*1011 Па, коэффициент Пуассона = 0.3, угловая скорость = 1.88*104 сек-1, I1 = 0.9*I3 , I3 = 0.968*10-8 кг м2, Кинетический момент L = 1.824*10-4 кг м2/с, логарифмический декремент затухания = 0.02. Опорные напряжение, подаваемые на электродами V0 = 450 B, относительно зазор между ротором и электродами d = 6*10–3. Пусть вектор кинетического момента лежит в плоскости 13. Угол, определяющий геометрический размер электродов, 0 = arccos(5/6). По формуле (2.60) получаем Mmax = 3,2* *10–4 г см2/с2. Это значение достигается, когда = /2 и когда вектор кинетического момента образуется осью 3 угол /4 или 3/4, т.е. 1,3 = 0,5. По формуле Mmax/L получаем величину возможно ухода электростатического гироскопа * = 3,5*10–2 град/час. Для современного прецизионного гироскопа существенным считается уход 10–310–5 град/час.
Проведем асферизацию с учетом «двойного вращение» ротора. Для этого введем функцию ur(, )
ur(, )= –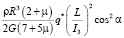 
(22)
где q* пока неизвестный коэффициент. Вычитая (22) из (7), имеем уравнении поверхности деформированного ротора в движении, близком к движению Эйлера-Пуансо, с учетом асферизации ротора [4]
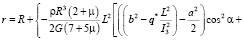
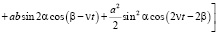(23)
Далее, проделывая аналогичные выкладки как и выше в рассмотренном случае, получим для M0 следующее выражение
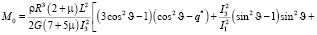
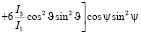(24)
Из (17) и (19) видно, что при M0 равном нулю, возмущающий момент, действующий на ротор электростатического поля, тоже обращается в нулю. Следовательно, приравнивая к нулю (24), можно найти значения q*, при котором момент будет равен нулю
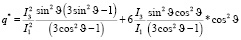(25)
Выводы
Из (25) видно, что переменный коэффициент q* имеет особенность при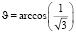 
. Следовательно, имеют место такие режимы движения ротора ЭСГ, при которых избавиться от возмущающих моментов, вызванных инерционными силами, при помощи асферизации, принципиально невозможно.