В работах [1, 2] было показано теоретически, что возможны устойчивые состояния атомов водорода в так называемых субатомных состояниях. Энергия связи таких состояний порядка 5•105 эВ, что на четыре порядка больше, чем для традиционных атомов водорода. Такие атомы занимают меньшую область локализации и могут с большей вероятностью вступать в ядерные реакции, что может послужить для объяснения наблюдаемых низкоэнергетических ядерных трансформаций, в частности, для объяснения анимального тепловыделения в «наводороженных» металлах [3, 4].
Возможность существования субатомных состояний атома водорода основана на использовании формулы де Бройля:
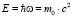(1)
Смысл этой формулы заключается в том, что элементарная частица с массой покоя m0 имеет собственную квантовую энергию движения с частотой . Эта формула предложена де Бройлем в 1923 году в своей докторской диссертации в виде гипотезы. Однако в последующем он показывал, что эта формула является инвариантной и удовлетворяет известным релятивистским преобразованиям, поскольку частота и масса частицы преобразуются по одинаковым законам и справедлива и при отсутствии поступательного движения квантовых частиц [5].
С учетом формулы (1) электрон в атоме водорода совершает, в том числе, движение за счет собственной энергии Е. Эта энергия описывает движение спина электрона и его пространственную локализацию [6]. Будем характеризовать это движение с помощью радиуса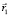 
относительно своего вероятностного центра. В свою очередь движение вероятностного центра электрона относительно протона за счет кулоновской энергии будем описывать с помощью радиуса 
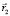, см. рис. 1.
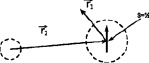
Рис. 1. Координаты атома водорода
Тогда уравнение движение электрона запишется в виде:
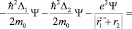
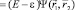(2)
Здесь - энергия связи электрона в атоме водорода. Если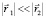 
, то кулоновскую энергию в (2) можно представить в виде:
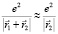
Тогда в уравнении (2) переменные разделяются и можно получить два уравнения:
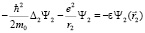(3)
Это уравнение описывает движение электрона в традиционном атоме водорода. Второе уравнение
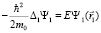(4)
описывает движение спина электрона и его пространственную локализацию. Волновая функция этого уравнения имеет вид [6]:
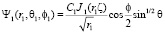(5)
и представляет собой стоячую неоднородную волну. Если вероятностные центры электрона и протона совпадают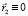 
, то из уравнения (1) получаем субатомное состояние водорода, которое рассмотрено в работах [1, 2]:
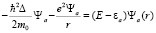(6)
Решение этого уравнения имеет вид:
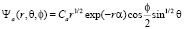(7)
Энергия связи равна:
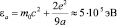(8)
Здесь боровский радиус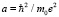 
. Это состояние имеет наибольшую энергию связи и устойчиво к взаимным смещениям вероятностных центров протона и электрона [7].
Рассмотрим конкретную систему пористый титан насыщенный водородом (это может быть и дейтерий). Будем нагревать эту систему до некоторой температуры, такой, что в спектре теплового излучения будет заметна ультрафиолетовая составляющая с длиной волны = 1,215•10–5 см. Это первая линия серии Лаймана. В этом случае атомы водорода будут переходить в возбужденные состояния, и туннелировать в зону проводимости титана, см. рис. 2. Работа выхода электрона из титана равна е = 3,95 эВ, что больше разницы между вакуумным уровнем водорода и первым возбужденным уровнем. Она равна 2 = 3,4 эВ. Таким образом, атомы водорода могут частично находиться в ионизованном состоянии. Со дна валентной зоны титана электроны с нулевой энергией поступательного движения могут переходить на субатомный уровень ионизованного водорода, при этом будет выделяться энергия равная ~ а в соответствии с (8). Преимущественный переход электронов на этот уровень связан с тем, что энергия Ферми электронов составляет f = 13,55 эВ и находится ниже основного уровня атома водорода, отсчитанного от вакуумного уровня 1 = 13,55 эВ.
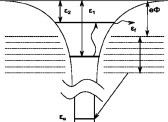
Рис 2. Энергетические диаграммы атома водорода и титана
Действительно, одна из компонент матричного элемента дипольного излучения для такого перехода не равна нулю
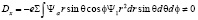(9)
Здесь – амплитуда электрического поля в волне. Переходы с основного уровня атома водорода в субатомное состояние в рассматриваемом приближении не возможны, поскольку в этой модели атома водорода не учитывается спин электрона. Более того, в этом случае речь идет по существу о спонтанных переходах, которые в природе не обнаружены.
Заметим, что для ионизации атомов водорода можно использовать и другие приемы, важно, что бы рядом был резервуар с фермиевскими электронами для обеспечения переходов в субатомные состояния ионизованного водорода.
Субатомы водорода могут приближаться к ядрам других элементов как нейтральные частицы на достаточно близкие расстояния, поскольку протон экранирован электронной оболочкой с большой собственной энергией. В сильном электрическом поле ядра с Z – номером в таблице Менделеева субатомы водорода поляризуются и могут приблизиться на расстояния порядка r0.
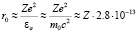см (10)
Для ядер титана с Z = 22 радиус сближения равен r0 6,2•10–12 cм.
Доставка протона в электронной оболочке на такие расстояния к ядрам должна заметно повысить вероятность ядерных реакций.
Таким образом, о существования субатомов водорода в рассматриваемой системе пористый титан + водород можно судить по косвенным признакам: появлению новых элементов и – излучению, которые могут проявиться при нагревании и экспозиции системы во времени. Результаты подобных первых экспериментов описаны в обзоре [8]. Облучая образцы с водородом ультрафиолетовым светом с заданной длиной волны, можно получить избирательный эффект генерации субатомов водорода. При этом заметим, что опуская возможный тепловой эффект от ядерных реакций, термолизация гамма-излучения может приводить к значительному энергетическому выигрышу.