Успехи, достигнутые при теоретических исследованиях ламинарно-турбулентного перехода в дозвуковых течениях [1], позволяют надеяться, что математический аппарат, разработанный в этом разделе механики, может быть применен к исследованию высокоскоростных потоков. Понимание природы физических процессов, сопутствующих нелинейной эволюции неустойчивых возмущений в таких пограничных слоях, помимо важного фундаментального значения для данного типа потока, создает необходимую основу перехода к аналогичным исследованиям при более высоких скоростях.
При теоретических исследованиях высокоскоростных потоков сжимаемого газа кроме рассмотрения возмущений скорости необходимо учитывать возмущения температуры и плотности. Связь теории и эксперимента обеспечивает сотрудничество с коллективом сверхзвуковой аэродинамической трубы Т-325 ИТПМ им. С.А. Христиановича СО РАН. В [2] исследован состав и продольная динамика возмущений на непроницаемых поверхностях при сверхзвуковом числе Маха. На основе изучения линейной стадий развития возмущений четко выявлены особенности, которые уже не могут быть отнесены к линейным. Так при невысоком уровне контролируемых возмущений реализуется субгармоническая неустойчивость, закономерности которой качественно и количественно описываются нелинейной моделью взаимодействия в резонансных триадах. В спектре возмущений преобладают трехмерные моды, а заполнение его представляет собой каскадный процесс выделения трехмерных субгармоник в параметрической области. В экспериментах установлено, что в начальном спектре возмущений фиксируются два волновых пакета с кратными частотами (частотой субгармоники f1 = 10 кГц и основной частотой гармоники f2 = 20 кГц) при этом доминирует пакет с f2. Волновые пакеты представляют собой волновые поезда широкого спектра по азмутальному волновому числу , в которых присутствуют трехмерные волны, распространяющиеся под углами – 90 ° 90 ° к направлению основного потока ( = arctg(/r); r – продольное волновое число), причем волновые поезда достаточно симметричны по во все исследуемом интервале. Вниз по потоку наблюдаетмя увеличение интенсивноси в основном двумерных волн и компонент с высокими . Эти компоненты имеют низкие линейные инкременты.
В данной работе проводится математическое описание данной ситуации в рамках теории возмущений гидродинамической устойчивости.
Параметры [2] являлись отправными при расчетах – рассмотрен пограничный слой при числе Маха М = 2, = 1.4, температуре торможения 310 К, числе Прандтля s = 0.72 и при единичном числе Рейнольдса Re1 = 12.5106 m-1. Интервал продольных чисел Рейнольдса соответствовал экспериментальному.
Основные соотношения и методы решения. Основные положения нелинейной модели взаимодействия возмущений в трехволновых резонансных системах в пограничных слоях сжимаемого газа подробно изложены в [3]. Обозначим через масштаб пульсационного поля ( << 1). Рассматриваются возмущенные поля скоростей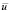 
, плотности 
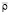, давления 
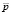и температуры 
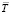сжимаемого газа:
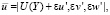
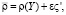
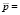
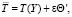
в безразмерной декартовой системе координат (X, Y, Z) = (x, y, z)/ ( =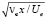 
– характерный масштаб, индекс e соответствует параметрам на внешней границе; величины со штрихами и без штрихов – пульсационные и средние величины). Решение строится с помощью разложения по малому параметру и двухмасштабному разложению продольной координаты. Помимо «быстрого» масштаба X вводится «медленный» масштаб = X, что обусловлено существенным различием скоростей изменения фазы и амплитуды возмущений.
Решения для волн ищутся в виде
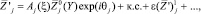
j = 1,2,3, (1)
где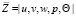 
– собственные амплитудные функции продольной, нормальной и трансверсальной компонент волновых скоростей, возмущения давления и температуры; A —медленно меняющаяся амплитуда; к.с. – комплексно-сопряженные величины;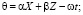 
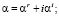i < 0 – инкремент; частота = 2f – вещественная величина; волновые числа , и частота связаны дисперсионным соотношением = (, ) линейной теории.
Из полной системы уравнений движения и законов сохранения для сжимаемого газа [4] в рамках слабонелинейной теории для вектора-функции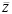 
получаем исходную рекуррентную систему для возмущений [3]:
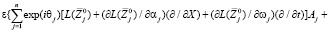
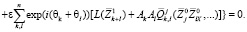(2)
Выражения для линейного оператора L имеют вид
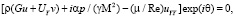
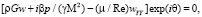
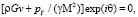(3)
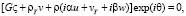
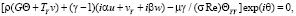
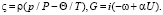
В (2), (3) М – число Маха на внешней границе пограничного слоя; = cP/cV – показатель адиабаты; = cpe/k – число Прандтля; k – теплопроводность;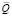 
– сумма нелинейных членов исходных уравнений.
Краевые условия для возмущений – {u, v, w, } = 0 при Y = 0, {u, v, w, } > 0 при Y > . При М = 2 толщина ламинарного пограничного слоя соответствует Y 7-8, а интегрирование проводится в интервале 0 Y Yk, Yk = 15. Все величины обезразмерены параметрам на внешней границе пограничного слоя; нормировка собственных функций:
.
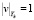Для возмущений первого порядка по на основе однородной системы восьмого порядка (3) (так называемой системы Дана – Линя) можно найти собственные значения при заданных , и числах Рейнольдса Re = x/ (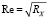
), а также определить собственные амплитудные функции линейных волн (1) при неопределенном амплитудном параметре A.
Решив данную краевую задачу на собственное значение, найдя при заданных Re, , и построив собственные амплитудные функции волн, законы развития возмущений в линейной области можно считать известными. Согласно слабонелинейной теории при указанных искомых параметрах нелинейность оказывает влияние только на амплитуду волны A.
В основе резонансной модели лежит процесс попарного взаимодействия волн в поле третьей волны в условиях синхронизации их фаз j = k + l. Во втором порядке по из неоднородных уравнений (2) можно найти возмущения более высокого порядка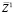 
, а также (используя условия разрешимости) построить амплитудные уравнения для резонансных триад, аналогичные системе, полученной в [3, 4]. Для простой трехволновой системы j–, k–, l–, волн (как правило, j k l) эти уравнения имеют вид
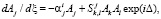
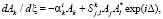(4)
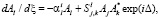
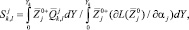
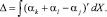
где – коэффициент фазовой синхронизации, учитывающий возможность расстройки по волновым числам в триплетах;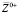 
– решения сопряженной к (3) системы уравнений.
В работе для каждой волновой моды безразмерный частотный параметр F, связанный с частотой зависимостью = ReF, а также приведенное безразмерное волновое число b = 103/Re являются постоянными. Рассматриваются как плоские (двумерные) волны с b = 0, так и косые (трехмерные) волны с b 0, имеющие на данной частоте максимальный инкремент.
В (4) начальные значения амплитуд Aj задавались через начальные интенсивности I волновых компонент. Связь между амплитудами колебаний и интенсивностью выражается через расчетное значение пульсаций массовой скорости m:
Ij(0) = Aj(0)mj(Ym)exp (– ij0).
Принимается, что в Ym значение пульсации массовой скорости m = u + U для преобладающей волновой компоненты (такая компонента определяется из амплитудно-частотного спектра возмущений) максимально. Численно рассчитывается значение средней массовой скорости U(Ym) и полагается, что начальные интенсивности Ij выражаются в долях U. Начальные значения амплитуд волн варьируются в широком диапазоне.
Результаты исследования и их обсуждения
Рассмотрим основные закономерности взаимодействия трех волн, связанных условиями фазового синхронизма. Сами триплеты могут быть двух видов – симметричные и несимметричные, в них 2D и 3D волны входят в разнообразных комбинациях. В данном случае наиболее представительны амплитуды 3D компонент на f2
А. Существование волны накачки. Установлено, что нелинейное взаимодействие наиболее эффективно, если одна из составляющих триплета является волной накачки [4, 5]. У такой волны максимальная начальная амплитуда, которая растет вниз по потоку в соответствии с линейным инкрементом. Пример выбора такой волны можно рассмотреть на рис. 1, где показаны линейные инкременты для 3D волн с разными азимутальными параметрами b.
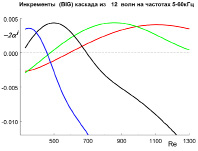
Рис. 1. Инкременты гармоники с разными b
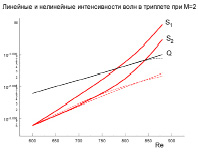
Рис. 2. Триплет 3D гармоники и субгармоник
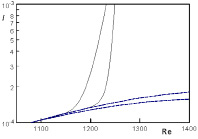
Рис. 3. Взрывное нарастание субгармоник
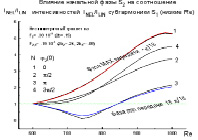
Рис. 4. Зависимость амплитуды субгармоники от начальной фазы
Б. При сближении амплитуд волн могут меняться как интенсивность, так и направленность передачи энергии. Очень хороший эффективный триплет показан на рис. 2. Триплет несимметричный, состоит из трех 3D волн, причем амплитуда гармоники (G) на f2 на порядок превышает амплитуды трехмерных субгармоник (S1 и S2) на f1. Штриховые линии показывают динамику субгармоник, развивающихся по линейному закону. Из рис. 2 видно насколько эффективно и быстро нелинейный процесс приводит к выравниванию амплитуд. Размеры сообщения не позволяют рассказать об интересных особенностях динамики всех трех волн при больших Re.
В. Существование каталитических режимов (амплитуда субгармоники может превышать амплитуду вынуждающей волны, не оказывая обратного влияния). При этом субгармоника получает энергию непосредственно из среднего течения. Обнаружено существование так называемых каталитических режимов, при котором реализуется очень быстрая (близкая к взрывному) нелинейная интенсивность субгармоник. Рис. 3 показывает один из вариантов такого взаимодействия. Конечно, сам пограничный слой, как естественный осциллятор, находит способы регулировать подобные всплески, но что они могут выявиться при моделировании необходимо знать.
Г. Важная роль отводится соотношению фаз взаимодействующих колебаний. Так как амплитуды (или интенсивности) представлены в комплексной области, обнаружена важная роль соотношения фаз волн в триплете. Найдено, что существуют варианты, где фаза практически не влияют на нелинейную эволюцию компонент триплетов, но есть триплеты, где ее роль значительна. На рис. 4 показан такой вариант. Найдены фазы максимальной передачи (близкие к нулевой) и фазы минимальной передачи (в противофазе). Как будет развиваться такая волна вниз по потоку зависит от интенсивности волны накачки. Если она значительна – волны скоро сблизятся по амплитуде, а если недостаточна, то так и будет наблюдаться два сценария развития субгармоники.
Д. Возможен режим «слабого» взаимодействия, когда невозможно определить, в какую сторону пойдет нелинейный процесс и что будет усиливаться. На рис. 5 показан один из возможных вариантов. Обычно он реализуется при малых интенсивностях гармоники.
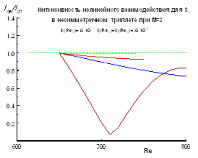
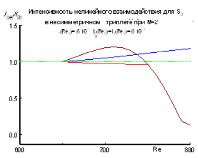
Рис. 5. Пример слабого взаимодействия; разный ход амплитуд при разных начальных I
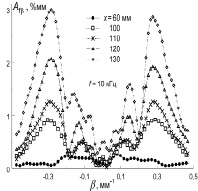
Рис. 6. Экспериментальная картина спектров субгармоники при разных Re (x)
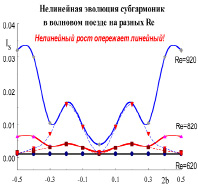
Рис. 7. Моделирование экспериментальной картины в групповом триплете (48 простых)
Итак, из этого необходимого предварительного рассмотрения можно сделать вывод, что нет такого триплета, который в одиночку может представить реальную динамику нелинейного взаимодействия в волновых поездах, результат заведомо будет не адекватен процессу. Оказалось, что необходимо учитывать возможно большее число компонент волнового поезда, включая как самые интенсивно растущие в линейном приближении, так и самые незначительные, на первый взгляд выпадающие из числа потенциальных участников, могущих повлиять на реальную картину. В данной работе был рассмотрен групповой триплет из 48 простых, учитывающий взаимодействия более 20 азимутальных компонент.
Рис. 6 описывает нестандартную сложную картину нелинейной динамики волнового поезда на f1. Аномалия заключается в том, что наиболее растущими выявлены не трехмерные компоненты с максимальными линейными инкрементами ( ~ 0.15), что обычно наблюдается, а компоненты высоких ( ~ 0.3), так называемые «хвосты», у которых очень низкие линейные инкременты. Такие компоненты обычно дают ничтожный вклад в энергетической картину волнового поезда. На возникающий вопрос – может ли моделирование взаимодействия в триплетах описать такую сложную аномальную динамику, дан положительный ответ, ясно видный из сравнения экспериментальной и расчетной картины (рис. 7). При рассмотрении надо учесть, что на экспериментальной картине даны размерные .