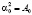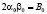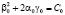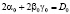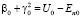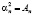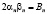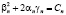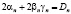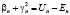Построим пример решения задачи со связями для одномерного стационарного уравнения Шрёдингера. Выберем 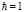 ,
, 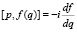 с помощью метода факторизации [1, 2].
с помощью метода факторизации [1, 2].
Как известно [1], уравнение Шрёдингера в координатном представлении
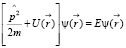 (1)
(1)
после введения цепочки лестничных пары лестничных операторов
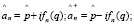
сводится к нелинейному операторному уравнению Риккати для операторной функции 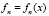 в координатном представлении:
в координатном представлении:
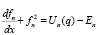 (2)
(2)
Цепочка операторов {En} образует спектр оператора Гамильтона
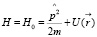 .
.
Для простоты, не будем писать «шляп» над операторами.
Цепочка операторов {Hn} факторизуется
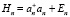 (3)
(3)
Для нахождения спектра En рассмотрим одномерное движение 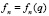 и построим III класс точно решаемых задач для полиномиальных потенциалов. В качестве примера, выберем одномерный потенциал 4 порядка
и построим III класс точно решаемых задач для полиномиальных потенциалов. В качестве примера, выберем одномерный потенциал 4 порядка
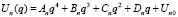 (4)
(4)
Будем искать решение уравнения (2) в виде
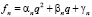 (5)
(5)
Подставляя (4), (5) в (2), получим таблицу алгебраических уравнений для коэффициентов (4), (5)
Таблица 1
Уравнения для нахождения коэффициентов цепочки на нулевом шаге математической индукции
|
q4 |
|
|
q3 |
|
|
q2 |
|
|
q |
|
|
q0 |
|
Таблица 2
Уравнения для нахождения коэффициентов цепочки на шаге n математической индукции
|
q4 |
|
|
q3 |
|
|
q2 |
|
|
q |
|
|
q0 |
|
Получили 5 известных коэффициентов цепочки An, Bn, Cn, Dn, En, и 3 неизвестных n, n, n.
Построим цепочку (3) явно.
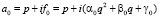
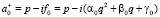 (6)
(6)
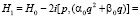
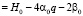 (7)
(7)
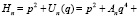
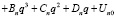 (8)
(8)
Здесь
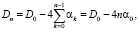
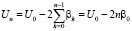 (9)
(9)
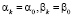
Используя табл. 1, 2, уравнения (8)-(9) получаем решения для последовательностей неизвестных {n}, {n}, {n}.
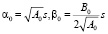 (10)
(10)
Где знак s = ± 1.
Первая степень q в табл. 2 приводит к алгебраическому уравнению
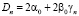 (11)
(11)
Из (9)-(11) следует уравнение
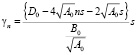 (12)
(12)
Уравнение для первой степени q из табл. 2 выглядит следующим образом
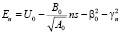 (13)
(13)
Подставляя (12) в (13) и перегруппировывая члены, получаем уравнение для спектра
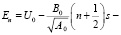
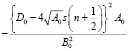 (14)
(14)
Из (14) видно, что по коэффициентам A0, B0 в спектре отсутствует предельный переход A0, B0 > 0. Тогда, как по классическому трению этот переход возможен. Операция D0 > 0 в (14) не запрещена.
В системе алгебраических уравнений из табл. 2 есть одна связь между коэффициентами. Выпишем её явно. Из строк при коэффициентах q3, q2 этой таблицы при значении квантового числа n = 0 возникают уравнения
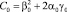
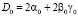 (15)
(15)
Разрешая (15) относительно 0, получаем связь между коэффициентами квантового осциллятора
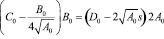 (16)
(16)
Для связи (16) справедливо отмеченное выше замечание относительно возможных предельных переходов.
Заметим, что из-за отсутствия предельных переходов по коэффициентам A0, B0.
В квантовой механике отсутствуют точные решения для полиномиальной потенциальной ямы третьего порядка и для поля вида
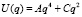 (17)
(17)
Вернёмся теперь к спектру (14).
Положим 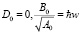
Тогда спектр (14) примет вид
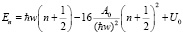 (18)
(18)
Отсюда видно, что размерность коэффициента 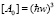 . Сам же объект, изучаемый в настоящей статье, в частном случае (18) является нелинейным квантовым осциллятором. Для этого объекта нет предельного перехода к классическому осциллятору как по постоянной Планка
. Сам же объект, изучаемый в настоящей статье, в частном случае (18) является нелинейным квантовым осциллятором. Для этого объекта нет предельного перехода к классическому осциллятору как по постоянной Планка 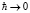 , так и по частоте колебаний w > 0.
, так и по частоте колебаний w > 0.
Выражаясь языком квантовой теории поля, можно сказать, что этот объект одновременно содержит как ультрафиолетовую расходимость w > и инфракрасную расходимость w > 0.
Отметим аналогию между построенным объектом и квантовой «бутылочкой», на которой обычно демонстрируется спонтанное нарушение симметрии квантовых полей.
Потенциальная яма существует для (16) в области значений коэффициентов 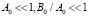 .
.
Выберем естественную систему единиц 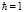 . Построим потенциальную яму и спектр значений энергии.
. Построим потенциальную яму и спектр значений энергии.
Для выбранной выше частоты w потенциальная яма имеет вид:
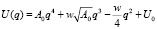 (19)
(19)
Спектр значений энергии в потенциальной яме (19) есть:
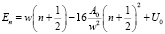 (20)
(20)
Выделяя полный квадрат, преобразуем (20) к виду легче поддающемуся графическому построению
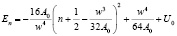 (21)
(21)
Потенциальная яма нелинейного осциллятора при значениях параметров А0 = 0,01, w = 2, |q| = r изображена на рисунке.
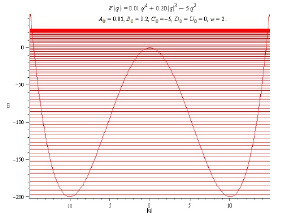
Потенциальная яма нелинейного осциллятора при значениях параметров А0 = 0,01, w = 2
Заключение
Методами нелинейной квантовой физики найден новый объект квантовой механики, являющийся решением стационарного уравнения Щредингера. Есть основания полагать, что этот объект является многоямным, то есть при других значениях параметров потенциальной энергии, являющейся полиномом 4 порядка, новые потенциальные ямы могут появиться в дополнение к введённой на рисунке. С точки зрения квантовой механики это будут новые физические объекты, статус которых в природе пока что неясен. «Бутылочка» рисунок широко применяется для описания свойств вакуума теории поля уже сегодня, как и линейное решение для осциллятора [2, 3]. Остаётся ждать вердикта эксперимента по поводу существования в природе этих новых существенно квантовых объектов.