Вопрос о параллельных прямых фактически сводится к вопросу о пятом постулате Евклида: является ли этот постулат независимым от других аксиом и постулатов геометрии Евклида, либо его можно вывести из них. Многочисленные попытки доказать это оказались безрезультатными [1, с. 13-15].
«Один из обнадеживающих способов подхода к доказательству пятого постулата, которым пользовались геометры XVIII и первой половины XIX вв., состоял в следующем: пятый постулат заменяется его отрицанием или каким-либо утверждением, эквивалентным отрицанию» [1, с. 15].
«Великий русский математик Н.И. Лобачевский (1792–1856), которому принадлежит честь открытия новой геометрии – геометрии Лобачевского, также начал с попытки доказательства пятого постулата. <…> один из эквивалентов пятого постулата состоит в утверждении, что через точку вне данной прямой проходит не более одной прямой, параллельной данной. Лобачевский заменил пятый постулат следующим:
Через точку вне прямой на плоскости проходят две прямые, не пересекающие данную» [1, с. 17-18].
Это предположение заключает в себе более глубокий геометрический смысл: Лобачевский фактически предположил, что параллельные прямые могут пересекаться. Это следует из Предложения 30 Евклида: «<Прямые>, параллельные той же прямой, параллельны и между собой» [2, с. 41].
Попробуем выяснить, при каких условиях это возможно. Возьмем произвольную прямую а (рис. 1).
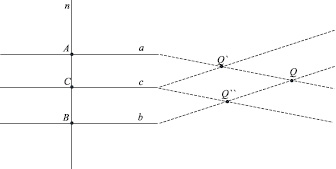
Рис. 1
Через произвольную точку A этой прямой проведем прямую n, перпендикулярную к ней, опираясь на Предложение 12 Евклида: «К данной неограниченной прямой из заданной точки, на ней не находящейся, провести перпендикулярную прямую линию» [2, с. 25]. На прямой n возьмем также произвольную точку B и через неё проведем прямую, параллельную исходной, что является возможным в соответствии с евклидовым Предложением 31: «Провести через данную точку прямую линию, параллельную данной» [2, с. 43]. Предположим, что прямые a и b пересекутся в точке Q. Теперь, выберем на прямой n ещё одну произвольную точку C, расположенную между точками A и B, и проведем через неё прямую с, параллельную a. Здесь возникает вопрос: где прямая c пересечет прямые a и b Предполагая, что расстояние до точек их пересечения зависит от расстояния между ними, приходим к выводу: прямая c пересечет прямую a в точке Q’, т.к. расстояние от прямой a до прямой c меньше чем до прямой b. С другой стороны, расстояние от прямой b до прямой c меньше чем расстояние до прямой a, значит точкой пересечения должна быть точка Q’’. Данное противоречие говорит о том, что, если параллельные могут пересекаться, то все они будут пересекаться в одной точке Q. Следовательно, прямая n является геометрическим местом точек, равноудаленных от одной точки, т.е. является окружностью. Таким образом, в тех геометриях, где прямыми являются окружности, например, в геометрии на сфере, параллельные могут, как пересекаться, так и нет, что и кроется в предположении Лобачевского: две из трёх параллельных, пересекаясь между собой, не имеют общих точек с третьей.
Что же касается доказательства пятого постулата Евклида, то сложилась довольно странная ситуация: единственность параллельной уже давно доказана, но на это не обратили внимания. Так, доказательство его Предложения 31 в современном изложении звучит следующим образом: «Для этого достаточно через точку X провести прямую c, перпендикулярную a, а затем через эту точку провести прямую b, перпендикулярную c» [1, с. 42].
Евклид следующим способом доказывает Предложение 12: «Пусть данная неограниченная прямая есть AB, а данная не находящаяся на ней точка C. Вот требуется к данной неограниченной прямой AB из данной не находящейся на ней точки С провести перпендикулярную прямую линию (рис. 2). Возьмём по другую сторону прямой АВ какую-нибудь точку D, из центра С раствором CD опишем круг EFH (постулат 3); прямую ЕН рассечём пополам в точке G (предложение 10) и соединим СH, CG, СЕ (постулат 1). Я утверждаю, что к данной неограниченной прямой АВ из данной не находящейся на ней точки С проведена перпендикулярная прямая CG» [2, с. 25-26].
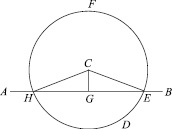
Рис. 2
Учитывая аксиому Гильберта: «Аксиома I2. Каковы бы ни были две точки A и B, существует не более одной прямой, которая проходит через эти точки» [1, с. 23], приходим к заключению: прямая CG определяется единственным образом. Теперь, проводя через точку C прямую, перпендикулярную к прямой CG, понимаем, что и она определяется единственным образом. Это означает одно: на плоскости через точку вне заданной прямой можно провести одну и только одну прямую, параллельную ей. Таким образом, пятый постулат является следствием первого постулата Евклида и аксиомы I2 Гильберта.

