Погрешность результатов при использовании математических вычислений может рассматриваться как следствие погрешности данных, округления или усечения. Аналогично, погрешность вычисления с помощью библиотечных процедур может быть следствием этих ошибок. Проблема анализа погрешности численных результатов – одна из фундаментальных в проблеме надежности вычислений [3].
Для получения предсказуемых и точных результатов важны следующие факторы: неточность внутреннего представления, неравномерность распределения вещественных чисел, вычитание. При операциях сложения и вычитания могут возникнуть такие ошибки как: потеря значащих цифр мантиссы у меньшего из чисел при выравнивании порядков, потеря крайней справа значащей цифры результата при сложении или вычитании мантисс, выход за границу допустимого диапазона значения того или иного вещественного типа при нормализации результата, большие и маленькие числа.
Для получения результата косвенного измерения выполняют математические операции, а потом округляют результат. Очевидно, что нет необходимости выполнять математические операции с результатами прямых измерений, как с точными числами, а нужно ограничивать их, получив определенное количество цифр в результате. Это облегчает работу, но при таких вычислениях возможны дополнительные погрешности. Чтобы погрешности вычислений не вносили искажений в конечный результат, необходимо брать их на порядок меньше погрешностей косвенных измерений. Поэтому все вычисления следует проводить с количеством значащих цифр, превышающим, как минимум, на единицу количество значащих цифр результатов измерений.
Поскольку аппаратно ЭВМ позволяет использовать лишь конечное подмножество чисел, то разумно соблюдать ряд правил [1], присущих арифметическим операциям. Эти правила более важны, чем требования обеспечения максимально возможной близости полученного результата к точному результату некоторой операции. Большое количество итерационных алгоритмов не требуют слишком высокой точности выполнения операций, но они оказываются неприменимыми при нарушении описанных выше правил.
На сегодняшний момент существует два способа проводить вычисления с большей точностью. Первый способ – точные значения заменяются приближенными, и проводится оценка погрешности исходных данных и округлений. У этого метода имеет ряд существенных недостатков. Второй способ – это интервальный анализ.
Интервальные вычисления – это достаточно разработанная область. Запись численного алгоритма производится на языках программирования, специально спроектированных с учетом требований интервальной арифметики. Такие языки называются SC-языками – от английского словосочетания «Scientific Computations», то есть «Научные Вычисления». За 70–90-е гг. было разработано целое семейство таких языков: PASCAL-SC и -XSC, FORTRAN-SC и -XSC, OBERON-XSC, MODULA-SC [4]. С помощью SC-языков разработаны различные пакеты численных методов, а написанные на этих языках программы используются для решения научно-технических задач.
Кроме того, существует несколько экспертных систем для математических расчетов посредством ЭВМ. Одно из них – приложение для математических и инженерных вычислений «Mathcad» корпорации PTC. При проведении численных расчетов (в отличие от символьных расчетов) Mathcad использует аппаратно реализованные арифметические инструменты самого компьютера, оперируя 64-битными числами с плавающей точкой. Именно отсюда проистекают все особенности и недостатки численных расчетов, которые на первый взгляд могут показаться следствием несовершенства самой программы [2].
Анализ точности вычислений на примерах вычислительной математики
В данном разделе рассмотрено несколько примеров математических вычислений, иллюстрирующих качество результатов расчетов в классических системах программирования («Turbo Pascal», «Free Pascal» и «Fortran G95»). Проанализируем точность проведенных вычислений, сравнивая их с экспертной системой «MathCAD».
Вычисления посредством системы «MathCAD»
Векторы и матрицы рассматриваются в системе «Mathcad» как одномерные и двумерные массивы данных.
Пример 1: А – матрица размера 2х3, В – матрица размера 3х3.
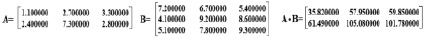
Пример 2: С – матрица размера 3х4, D – матрица размера 4х2.
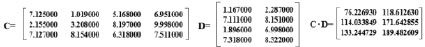
Пример 3: Е – матрица размера 7х5, F – матрица размера 5х6.
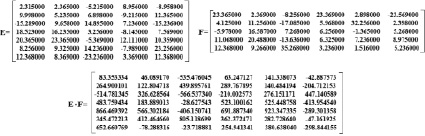
Пример 4: Пусть задана матрица T размером 5*5 и матрица Q размером 5*5. Пусть элементы матриц – дробные числа с точностью 6 знаков после запятой. Выбор шести значимых цифр после запятой обоснован достаточной точностью для большинства реально получаемых экспериментальных данных.

Однако результат перемножения матриц представим в виде таблицы чисел с 12 выводимыми разрядами.
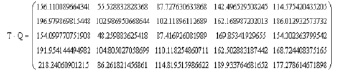
Вычисления посредством систем программирования Pascal и Fortran
Для сравнения падения точности расчетов при большом количестве арифметических операций были написаны программы, реализующие перемножение матриц.
При вводе элементов матриц из вышеприведенных примеров 1-3 результирующие матрицы совпадают с матрицами, полученными в системе «MathCad».
Сравнивая результаты расчетов примера 4 с результатом, полученным при перемножении этих матриц в программе MathCAD, можно сделать следующие выводы:
1) При перемножении матриц T и Q с использованием компилятора Turbo Pascal в случае, когда элементы матриц – дробные числа типа single, в результирующей матрице точность элементов – 4 знака после запятой;
2) Результат перемножения матриц T и Q с использованием компилятора Turbo Pascal (элементы матрицы – дробные числа типа real. Вывод осуществлялся с точностью 11 знаков после запятой):

Видно, что восьмой знак после точки уже округлен. Для матриц с размерами меньше, чем 2*3 и 3*3, результирующая матрица на выходе имеет 9 знаков после запятой. Однако, для матриц этих же размеров, но с элементами с большим числом знаков после запятой, элементы результирующей матрицы имеют округление в девятом знаке после запятой;
3) При перемножении матриц T и Q с использованием компилятора Turbo Pascal в случае, когда элементы матриц – дробные числа типа double, в результирующей матрице точность получаемых элементов – 8 знаков после запятой.
4) Результат перемножения матриц T и Q с использованием компилятора Turbo Pascal (элементы матрицы – дробные числа типа extended. Вывод осуществляется с точностью 11 знаков после запятой):

Одиннадцатый знак округлен!
5) Результат перемножения матриц T и Q с использованием компилятора Free Pascal (элементы матрицы – дробные числа типа real, вывод осуществляется с точностью 11 знаков после запятой) аналогичен результату перемножения матриц T и Q с использованием компилятора Turbo Pascal при использовании типа данных extended для элементов матриц. При использовании элементов матрицы типа extended , результат не меняется.
Можно сделать вывод о том, что при использовании дробных чисел типа extended или при использовании компилятора Free Pascal, а не Turbo Pascal, точность расчета результирующей матрицы повышается.
6) Результат перемножения матриц T и Q при использовании компилятора Fortran G95 (элементы матрицы – дробные числа типа real*4 – 4 байта):

Видно, что 5-6 знак после запятой округлен.
7) Результат перемножения матриц T и Q при использовании компилятора Fortran G95 (элементы матрицы – дробные числа типа real*8 – 8 байт):

Элементом результирующей матрицы является число с точностью восемь знаков после запятой. Девятый знак округлен.
8) Результат перемножения матриц T и Q при использовании компилятора Fortran G95 (элементы матрицы – дробные числа типа real*10 – 10 байт):
Элементом результирующей матрицы является число с точностью четырнадцать знаков после запятой.
Таким образом, можно сделать следующие выводы:
– В экспертной системе MathCad результат выводится с точностью 12 знаков после запятой без ошибок и округлений;
– Компилятор Turbo Pascal делает округление вещественных чисел типа real в восьмом знаке после запятой;
– В результате перемножения двух матриц с элементами типа extended с помощью компилятора Turbo Pascal округление происходит в одиннадцатом знаке после запятой;
– При использовании компилятора Free Pascal округление элементов результирующей матрицы происходит в одиннадцатом знаке после запятой, независимо от типа элементов исходных матриц – real или extended. Точность не зависит от типа данных, т.к. во Free Pascal тип real занимает 8 байт, а не 6, как в Turbo Pascal. (Free Pascal использует математический сопроцессор (или эмуляцию) для всех вычислений с плавающей точкой. Размер стандартного типа Real зависит от процессора и является либо Single, либо Double);
– В результате перемножения двух матриц с элементами типа Real*4 с помощью программы, написанной на языке Fortran, округление происходит в пятом или шестом знаке после запятой;
– При использовании компилятора Fortran G95 в результате перемножения двух матриц с элементами типа Real*8 округление происходит в девятом знаке после запятой;
– При использовании Fortran G95 в результате перемножения двух матриц с элементами типа Real*10 округления не происходит вплоть до пятнадцатого знака после запятой.
Метод наименьших квадратов
МНК – один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.
Рассмотрим следующую задачу: аппроксимировать степенным полиномом набор из восьми экспериментальных точек (таблица).
|
х |
1.123456 |
2.258741 |
2.423658 |
2.725369 |
3.123655 |
3.128795 |
4.259965 |
5.302547 |
|
у |
24.861238 |
33.568903 |
34.112533 |
36.555926 |
47.012618 |
60.024471 |
129.145676 |
195.688218 |
Показать, что результат вычислений будет также определяться типом входных и выходных переменных в рассматриваемых языках программирования.
Так как условие минимального отклонения значений функции от экспериментально полученных точек есть равенство нулю частных производных функции, то, решив систему уравнений, составленную из этих частных производных, можно найти приближенную зависимость в виде полинома.
Проведем аппроксимацию полиномом 5-й степени.
а) Результат вычислений в виде вектора коэффициентов С в программе MathCAD:

Величина среднеквадратичного отклонения значений полинома и таблично заданной функции: 9.079724068764.
б) Результат вычислений в Turbo Pascal, тип входных данных – single, тип выходных данных (погрешности) – real:

Отклонение с точностью 5 знаков после запятой.
в) Результат вычислений в Turbo Pascal, тип входных данных – double, тип выходных данных (погрешности) – real:

Отклонение с точностью 5 знаков после запятой.
г) Результат вычислений в Turbo Pascal, тип входных данных – single, тип выходных данных (погрешности) – single:

Отклонение с точностью 0 знаков. То есть, все знаки после разделителя целой и дробной частей не верны!
д) Результат вычислений в Turbo Pascal, тип входных данных – double, тип выходных данных (погрешности) – double:

Отклонение с точностью 5 знаков после запятой.
е) Результаты вычислений при использовании компилятора Free Pascal полностью совпадают с результатами, полученными при использовании компилятора Turbo Pascal.
Таким образом, можно сделать следующие выводы:
– тип переменных для входных данных не влияет на точность результатов;
– тип данных размером 4 байта непригоден для выходных переменных в случаях расчетов, содержащих множественное возведение в степень и операции с матрицами;
– результат необходимо представлять только переменными, имеющими размер не ниже 6 байт, в этом случае точность результатов будет в пределах 5-6 знаков после запятой;
– при использовании входных данных с количеством знаков после запятой от 0 до 6 точность результата неизменна.
Заключение
На основании вышеизложенного можно сделать следующие выводы:
– Использование типа переменных размером 4 байта для научных расчетов нецелесообразно, так как результирующая точность при использовании переменных одинарной точности составляет не более 4 знаков после запятой. Тип данных размером 4 байта также непригоден для выходных переменных в случаях расчетов, содержащих множественное возведение в степень и операции с матрицами, так как происходит быстрое накопление погрешности и в некоторых случаях в результате будет верна лишь целая часть.
– Для большинства расчетов минимально и достаточно использовать для представления данных переменные с двойной точностью (8 байт), т.к. они дают точность не менее 5 знаков после запятой, что вполне достаточно для большинства научных исследований;
– Входные и выходные данные, а также все промежуточные данные, должны быть приведены к одному типу. Для получения результатов с двойной точностью все входные и выходные данные, а так же все константы, должны иметь двойную точность;
– Очевидно, что необходимо сводить к минимуму число необходимых арифметических операций. Например, умножение дробных чисел – часто самая неточная операция, сразу дающая ошибку в четвертом знаке результирующего числа. Также следует избегать вычитания. Особенно следует остерегаться вычитания очень близких друг к другу чисел;
– Чтобы погрешности вычислений не вносили искажений в конечный результат, необходимо брать их на порядок меньше погрешностей косвенных измерений. Поэтому все вычисления следует проводить с количеством значащих цифр, превышающим на единицу количество значащих цифр результатов измерений;
– При относительной погрешности результата косвенных измерений порядка 10-100 % вычисление можно проводить с двумя значащими цифрами. При относительной погрешности порядка 1-10 % – с тремя значащими цифрами. При относительной погрешности порядка 0.1-1 % – с четырьмя значащими цифрами.

